1. Introduction to Machine Learning

Machine Learning(ML)

• A branch of artificial intelligence, concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data

머신러닝을 한 문장으로 요약하면
Improve on task T, with respect to performance metric P, based on experience E.

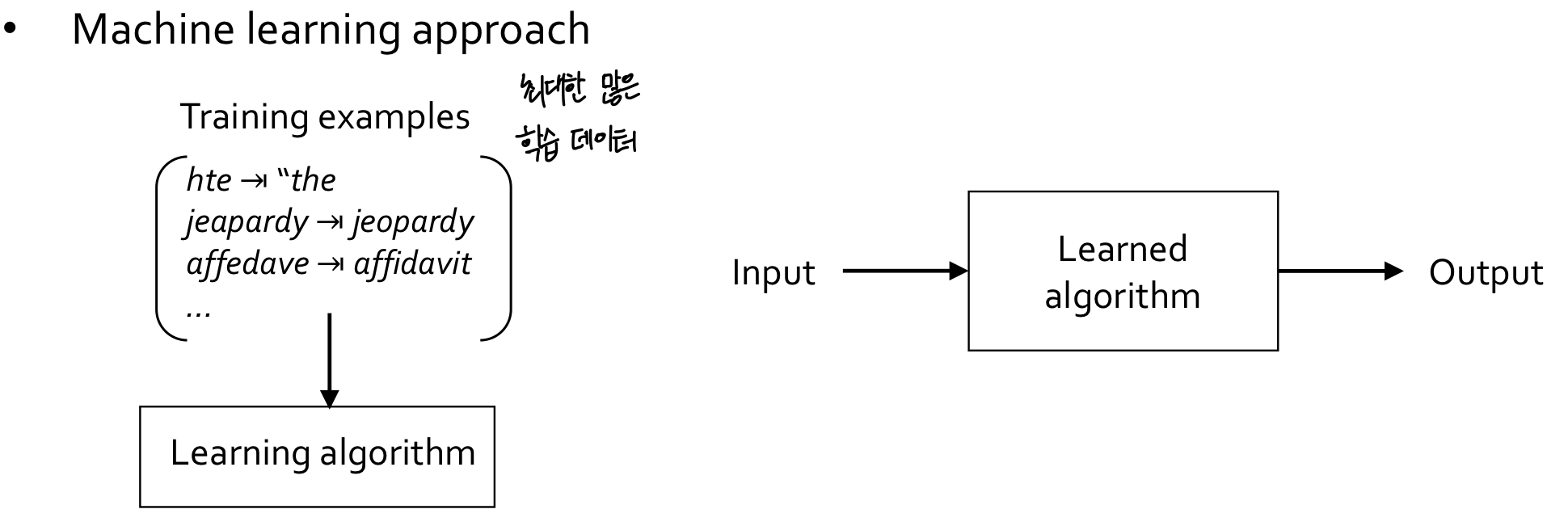
• Key idae: Generalization!

Generalization

• Definition of learning
  • A form of abstraction where common properties of specific instances are formulated as general concepts or claims
  • It extracts the essence of a concept based on its analysis of similarities from many discrete objects
  • If a toddler had never seen a willow tree or pine tree before he still might classify it as a tree because it's green
• Objective of learning
  • Not to learn an exact representation of the training data itself
  • To build a statistical model of the process that generates the data

→ 기계학습을 하는 목적은 일반화.
trainig data에 대해서 잘 되는게 목표가 아니라, 이 training data로 부터 어떤 패턴을 배원서 우리가 training data에서 보지 못한 새로운 data가 오더라도 잘 하길 기대하는 것.

No Free Lunch Theorem for ML

• No machine learning algorithm is universally any better than any other
• Do not try to seek a universal learning algorithm (No absolute best algorithm)
• 어떤 기계학습 알고리즘도 다른 기계학습 알고리즘보다 항상 좋다고 말할 수 없다.

Types of Learning

• 지도학습(Supervised Learning): 지도 학습은 각 입력값에 대한 적절한 출력을 알려주는 학습 데이터가 제공됩니다. 이러한 방식은 분류(Classification)와 회귀(Regression) 문제를 해결하는 데 주로 사용됩니다.
• 비지도학습(Unsupervised Learning): 비지도 학습은 출력값 없이 입력값만 제공되며, 이러한 방식은 패턴 인식, 군집화(Clustering) 또는 차원 축소(Dimensionality Reduction) 등의 문제를 해결하는 데 사용됩니다.
• 반지도 학습(Semi-supervised learning): 머신러닝의 한 유형으로, 지도 학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)의 중간 형태라고 볼 수 있습니다.
  이 방법은 레이블이 지정된 데이터(지도 학습에 사용되는)와 레이블이 지정되지 않은 데이터(비지도 학습에 사용되는)를 모두 사용하여 모델을 학습시킵니다. 일반적으로 레이블이 지정된 데이터는 많지 않고, 레이블이 없는 데이터는 풍부한 경우에 사용됩니다.
  이러한 접근 방식의 주요 이점은 레이블이 지정된 데이터를 사용하여 모델을 학습시키는 동시에, 레이블이 없는 데이터에서도 유용한 패턴과 구조를 학습하는 데 있습니다. 이는 모델의 성능을 향상시키고 일반화 능력을 개선하는 데 도움이 됩니다.
  예를 들어, 어떤 이미지 분류 작업에서 사람이 직접 레이블을 지정하는 것은 시간과 비용이 많이 들 수 있습니다. 이런 경우, 작은 양의 레이블이 지정된 데이터로 모델을 초기 학습시킨 후, 레이블이 없는 데이터를 사용하여 추가적인 학습을 수행하는 방식이 효과적일 수 있습니다.
• 강화학습(Reinforcement Learning): 강화 학습은 환경과 상호작용하며 학습하는 방식으로, 시스템(에이전트)이 어떤 행동을 취하면 환경에서 피드백(보상 또는 처벌)을 제공합니다.

Semi-supervised Learning

• Some of training data includes desired outputs
  • One of the bottlenecks of learning is the labeling of exmaples
  • Often done manually and time consuming
  • Can we label only a small number of exmaples and make use of a large number of unlabeled examples to learn? Possible in many cases!
• Two scenarios
  • LU learning: Learning with a small set of Labeled exmaples and a large set of Unlabeled examples.
    • 몇 개의 데이터는 Label을 주고, 나머지 데이터에 대해서는 안 줌.
  • PU learning: Learning with Positive and Unlabeled examples (no labeled negative examples)
    • One-classification의 일종. 정상 class의 데이터만 label을 줌.

Why Semi-supervised Learning Helpful?

• Similar data points have similar labels
  • Unlabeled data can help identify the boundary more accurately
    

2. Bias and Variance

Formal Definitions of ML

• Given training data and selected model class(a.k.a hypothesis class)
  $S= {(x_i,y_i)}_{i=1}^N, x \in \R^D, y \in \{-1, 1\} \\ h(x|w,b) = w^Tx + b$
• Goal: find (w, b) that predicts well on S
  → 파라미터 찾기
• Loss function
• Learning objective (optimization)
  $argmin_{w,b} \sum^{N}_{i=1}L(y_i,h(x_i|w,b))$

Generalization

• Generalization in ML 기계학습의 일반화
  • An ML model's ability to perform well on new unseen data rather than just the data that it was trained on
  • Learning algorithm maximizes accuracy on training exmaples
  • How to generalize from training to test?
• Strongly related to the concept of overfitting
  • Overfitting = poor generalization
    

Generalization Error

• Objective of learning
  • Not to learn an exact representation of the training data itself
  • To build a statistical model taht generates the data
• True distribution: $P(x,y)$
  • All possible cases - unknown to us
  • Train and test data are generated by $P(x,y)$
  • Assumption: iid(independent and identically distributed)
    (→ independent = 데이터 하나하나를 얻는 과정이 독립,
    identically distributed = 데이터 분포가 바뀌지 않음)
• Train: Fit a hypothesis $h(x)$
  • Using training data $S$ = ${(x_i, y_i)}_{n=1}^N$, sampled from $P(x,y)$
• Generalization Error: $L_p(h) = E_{p(x,y)}[L(y, h(x))]$
  • Prediction loss on all possible cases
  • Generalization: ability to perform well on previously unseen input
• Underfitting: Generalization error < Training error
  • The training error is not sufficiently low
• Overfitting: Generalization error > Training error
  • The gap between the training and test error is too large
• Training an ML algorithm well
  • 1. Make the training error small
  • 2. Make the gap between the training and test error small

Occam's Razor 오컴의 면도날 이론

• All things being equal, the simplest solution tends to be the best one
• The simplest explanation tends to be the right one.
  = 간단한 걸 선택하는게 맞다.

Typical Relation between Capacity and Error

• Informally, a capacity is the funtion's ability to fit a wide variety of functions
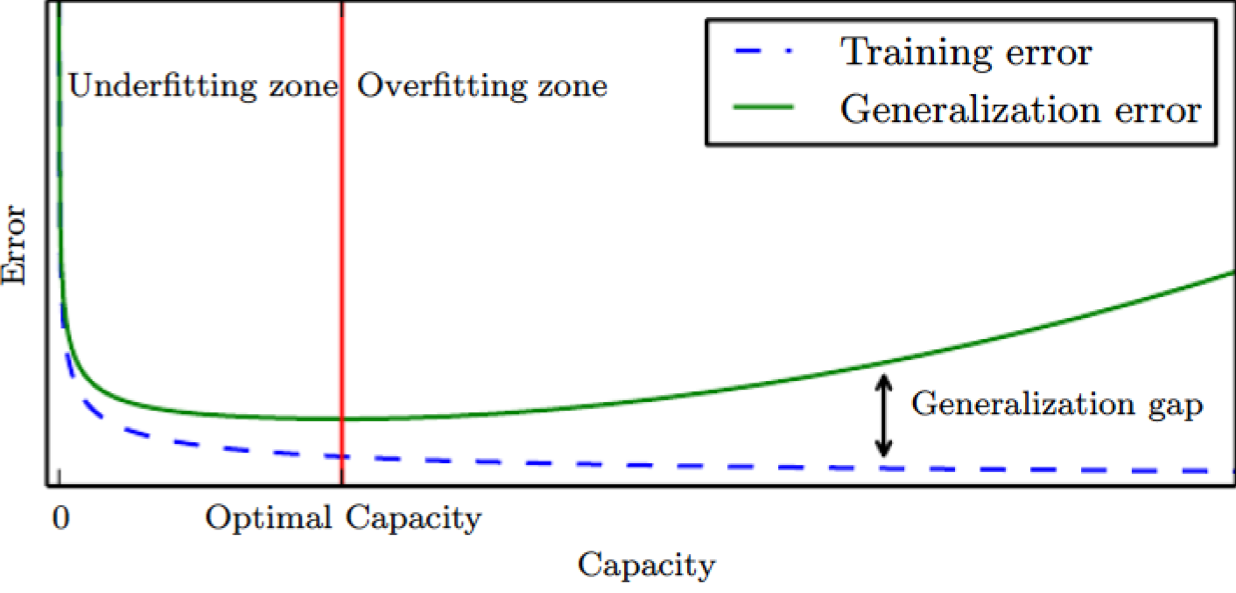
  • As capacity increses, training errors decreases but the gap increses.
    

Regularization

• Given an ML algorithm, a preference for one solution in its hypothesis space to another
  • e.g., weight decay in a linear regression
    $J(w) = (error) + \lambda w^Tw$
    *$\lambda$ controls the strength of a preference for smallest weight
  • $\lambda=0$ : no preference, a large $\lambda$ : a smaller weight
  • The penalty term is called as a regularizer
• The main objective of regularization is to reduce its generalization error but not its training error

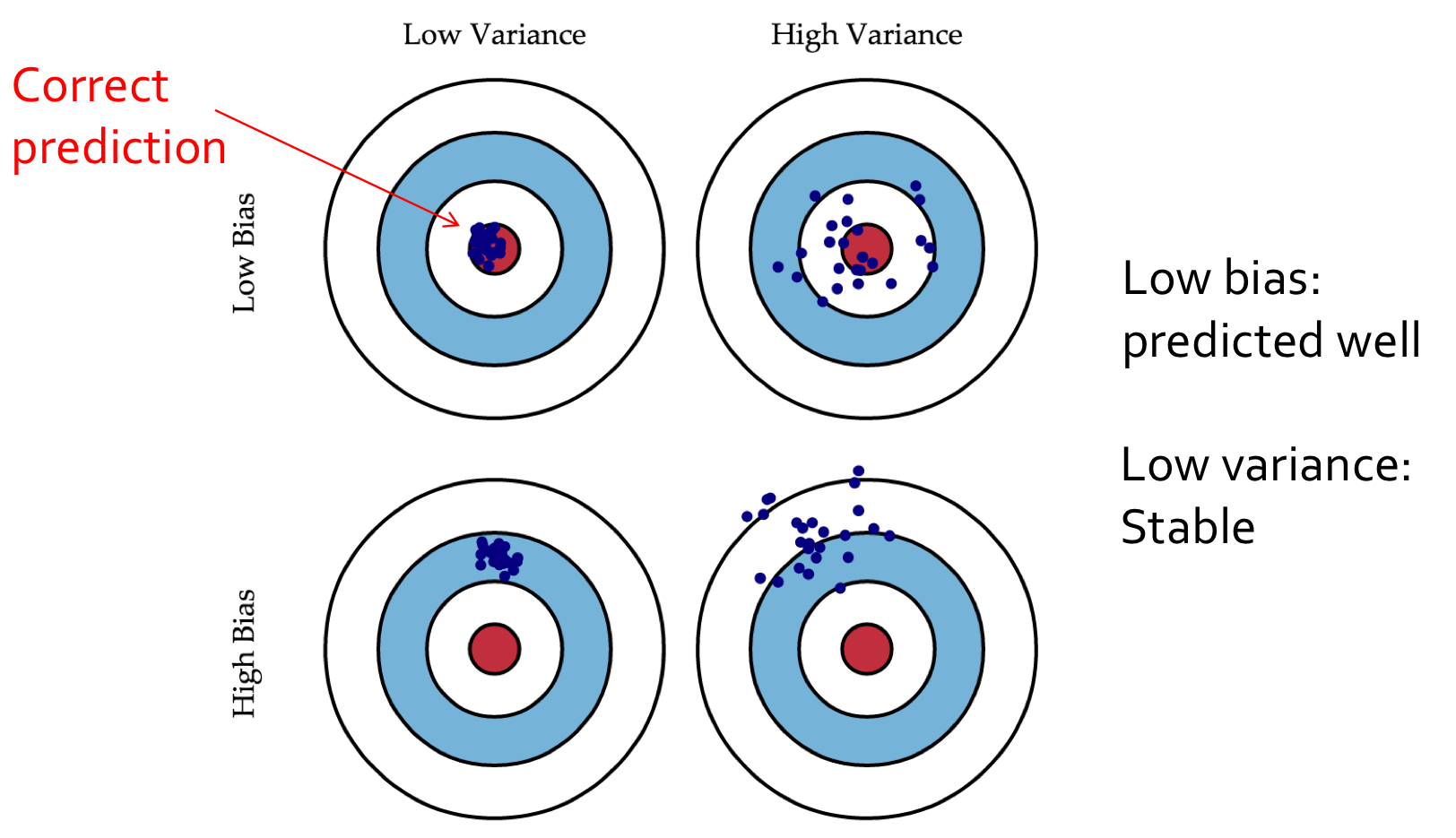
Bias/Variance Decomposition

(Source) http://scott.fortmann-roe.com/docs/BiasVariance.html

Trade-off between Bias and Variance

• Two sources of error in an estimator: bias and variance
  • e.g., weight decay in a linear regression
    $(Test Error) = (Bias) + (Variance)$
  • Bias: Expected deviation from the true value of the function
  • Variance: Deviation from the expected estimator values obtained from the different smapling of the data
• Increasing capacity tends to increase variance and decrease bias

Overfitting vs Underfitting

• High variance implies overfitting
  • Model class unstable
  • Variance increases with model complexity
  • Variance reduces with more training data
• High bias implies underfitting
  • Even with no variance, model class has high error
  • Bias decreases with model complexity
  • Independent of training data size

Recent Progress of Large Language Models