Robotics 5. Velocity Kinematics and Statics (작성중)

woobin Robot·2023년 10월 21일

Modern Robotics

목록 보기

5/5

4장의 forward kinematics(정기구학)에서는 로봇의 관절 값을 이용하여 엔드 이펙터의 좌표를 구해보았다.
Velocity kinematics (속도 기구학)에서는 관절의 값과 속도에 대한 엔드 이펙터의 속도를 다뤄볼 것이다.

이 속도 기구학에서 로봇공학에서 중요한 개념인 Jacobian이 등장한다.

엔드 이펙터의 configuration을 최소한의 좌표 $x\in\mathbb{R}^m$ , 관절의 값을 $\theta\in\mathbb{R}^n$ 로 표현했을때 forward kinematics를 다음과 같이 표현할 수 있다.

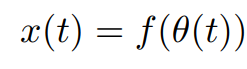
우리는 엔드 이펙터의 속도를 다룰거기 때문에 이 식을 시간에 대해 미분해보자

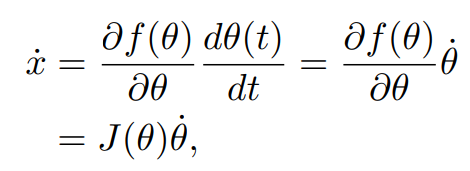
여기서 $J$ 가 Jacobian이다.
Jacobian은 위의 식에서 볼수 있듯이 관절 값 $\theta$ 에 대한 함수이며 관절의 속도 $\dot{\theta}$ 에 대한 엔드 이펙터의 속도 $\dot{x}$ 의 기울기이다.

구체적인 예를 한번 들어보자

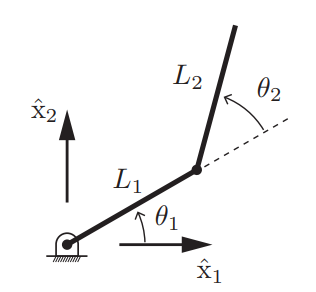
위 그림과 같이 2R로봇이 있을 때 forward kinematics를 다음과 같이 표현할 수 있다.

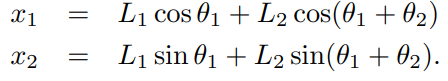
속도를 구하기 위해 시간에 대해 미분을 하고

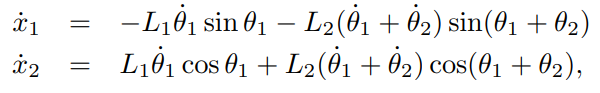
$\dot{x}=J(\theta)\dot{\theta}$ 형태로 바꾸면 다음과 같다.

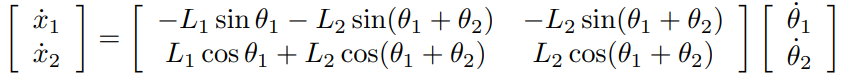
이와 같이 평면 로봇의 경우 삼각함수를 이용하여 쉽게 Jacobian을 구할 수 있다.

📖Jacobian의 특이점

자코비안을 사용할 때 조심해야하는 특이점이 있다.

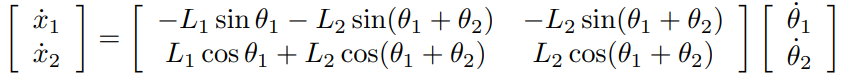
위에서 구한 2R 로봇 Jacobian의 열 벡터를 $J_1$ , $J_2$ 로 나타내고 행렬 곱을 선형 결합 형태로 나타내보자.

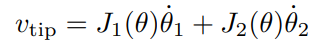
$v_{tip}$ 은 문자 그대로 로봇의 끝부분 즉 엔드 이펙터의 속도인 $\dot{x}$ 이다.
이 식으로 보면 $J_1$ 은 관절1의 속도 $\dot{\theta}_1$ 로 인해 발생하는 엔드 이펙터의 속도,
$J_2$ 은 관절2 속도 $\dot{\theta}_2$ 로 인해 발행하는 엔드 이펙터의 속도이고 이 값을 모두 더하여 실제 엔드 이펙터의 속도를 구하는 것을 볼 수 있다.
$J_1$ , $J_2$ 을 열 벡터로서 다음과 같이 그림에 나타낼 수 있는데

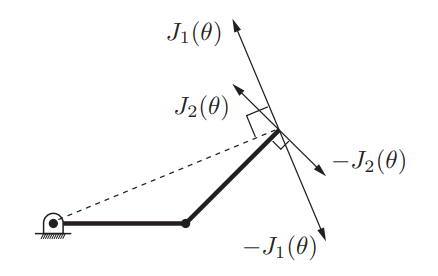
그림에 있는 $J_1$ , $J_2$ 가 서로 선형 독립이기 때문에.

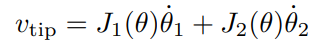
이 식처럼 엔드 이펙터의 속도 $v_{tip}$ 을 벡터 $J_1$ , $J_2$ 의 선형 결합으로 생각해볼 때 $\dot{\theta}$ 의 제한이 없다고 가정한다면 $J_1$ , $J_2$ 은 2차원 전체를 span함으로 엔드 이펙터는 어느 방향으로든 속도를 발생시킬 수 있다.

하지만 문제는 $J_1$ , $J_2$ 가 선형 의존일 때이다.
2R로봇의 경우에는 $\theta_1$ 의 값과 상관없이 $\theta_2$ 의 값이 0 또는 $\pi$ 일때 $J_1$ , $J_2$ 가 동일 선상에 놓이게 되면서 선형 의존이 되는데
두 벡터가 선형 의존임으로 $\dot{\theta}$ 으로 아무리 span을 해봐도 한 방향으로의 벡터만을 만들 수 밖에 없다. 즉 엔드 이펙터의 속도가 발생할 수 없는 방향이 나타나게 된다.
이런 상태의 Jacobian은 특이행렬(singular matrix)이 되며(역행렬이 존재하지 않는다.)
이런 로봇의 configuration을 특이점(singularities)이라고 한다.

📖manipulability ellipsoid

우리는 여기서 Jacobian을 이용하면 관절 속도의 제한이 주어졌을 때 그에 대한 엔드 이펙터의 속도 제한을 구할수 있지 않을까? 라는 생각이 들 수 있다.

그렇다면 다음과 같이 2R로봇의 관절 속도를 $\theta_1^2+\theta_2^2=1$ 로 제한했을 때의 $v_{tip}$ 의 한계를 나타내 보자

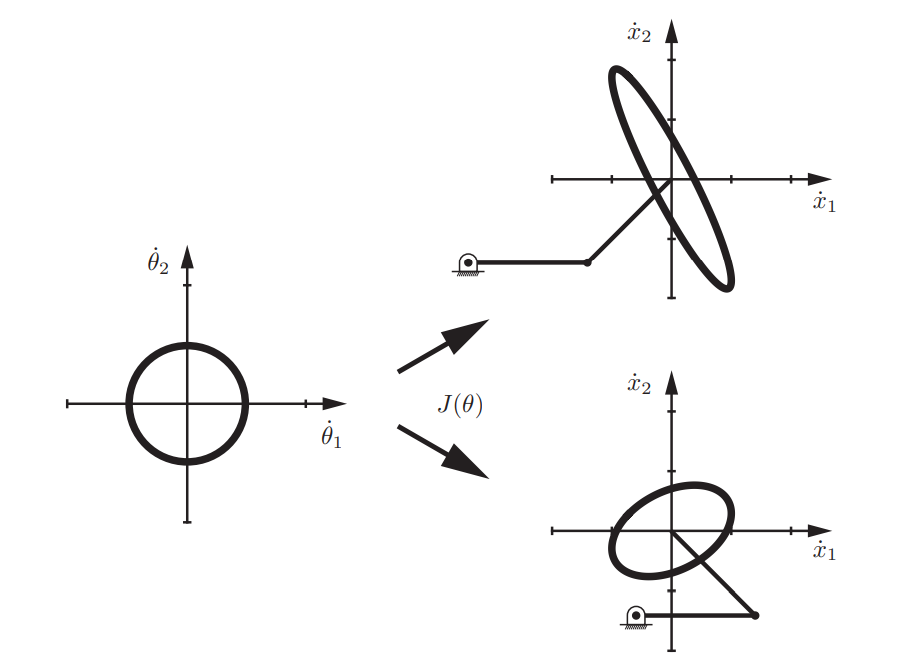
이 그림과 같이 관절 속도 공간의 경계선이 단위 원으로 주어진다면 $v_{tip}$ 의 경계선은 타운으로 나타나고 이는 로봇의 configuration에 따라 달라진다는 것을 볼 수 있다.
(이렇게 관절 속도의 제한을 단위 원으로 표현하는 것은 엑추에이터의 총(최대) 힘을 각 관절 속도의 제곱의 합으로 주어졌을때를 예로 들 수 있다.)
이 타원을 manipulability ellipsoid(조작성 타원체)라고 부른다.

📌manipulability ellipsoid의 사용

조작성 타원체의 모양을 보면 로봇의 특정 configuration에서 엔드 이펙터가 어느 방향으로 속도를 내기 쉬운지 알 수 있으며
조작성 타원체가 한쪽 방향으로 눌려 선분에 가까워진 모양이 될수록 그 configuration은 특이점에 가까워진다. 특이점에 얼마나 가까운지를 정량적으로 파악할 수 있는데 그 중 하나의 방법이 조작성 타원체의 장축과 단축의 길이( $l_{max}$ , $l_{min}$ )를 비교하는 것이다.

타원체가 원에 가까울 수록 즉 $l_{max}$ / $l_{min}$ 가 1에 가까울 수록 엔드 이펙터는 모든 방향으로 움직이기 쉬워지고 특이점에서 멀어진다.
$l_{max}$ / $l_{min}$ 가 클수록 특이점에 가까워 진다.

📖정역학 분석에서 Jacobian의 활용

이런 Jacobian은 정역학적 분석에서도 사용될 수 있다.
만약 엔드 이펙터의 어떠한 외력이 작용됐고 이 외력을 버티기 위해 필요한 관절 토크는 얼마일지 구해보자
정적평형 상태를 가정하고 로봇을 움직이는 어떠한 외력도 작용하지 않는다면 에너지 보존 법칙에 의해 엔드 이펙터에서 측정되는 일률과 관절에서 생성되는 일률은 똑같을 것이다.
엔드 이펙터에 작용되는 외력을 $f_{tip}$ , 관절 토크를 $\tau$ 라고 할때 에너지 보존 법칙을 다음과 같이 세울 수 있다.

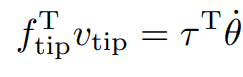
$v_{tip}=J(\theta)\dot{\theta}$ 을 대입하면

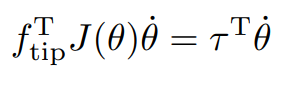
정적평형 상태를 가정했기 때문에 $\dot\theta$ 는 0이다. 하지만 이를 0에 무한히 가까운 값이라고 생각하면 다음과 같이 $\tau$ 에 대해 정리 할 수 있다.

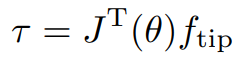
이 식을 이용하여 정적 평형 상태일 때 엔드 이펙터의 특정 힘을 내기 위해 필요한 관절 토크를 구할 수 있다.

📌force ellipsoid

Jacobian을 이용하여 관절 토크와 엔드 이펙터에서 발생하는 힘의 관계를 구해봤다.
Jacobian 전치행렬의 역행렬이 존재한다면 이 관계를 다음과 같이 $f_{tip}$ 에 대해 정리할 수 있고

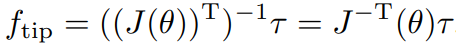
이 식을 이용하여 manipulability ellipsoid 때와 같이 관절 토크 제한을 단위원으로 표현했을때의 엔드 이펙터 힘( $f_{tip}$ )을 나타내 보자

$v_{tip}$ 일때와 같이 $f_{tip}$ 도 타원체로 표현이 되는데 이 타원체를 force ellipsoid(힘 타원체)라고 부른다.

이 힘 타원체의 모양을 보고 특정 로봇의 configuration에서 각 방향으로 엔드 이펙터의 힘을 얼마나 쉽게 발생시킬 수 있는지 알 수 있다.

📌manipulability ellipsoid 와 force ellipsoid 의 비교

이제 같은 configuration에서 조작성 타원체와 힘 타원체는 어떤 관계가 있는지 알아보자

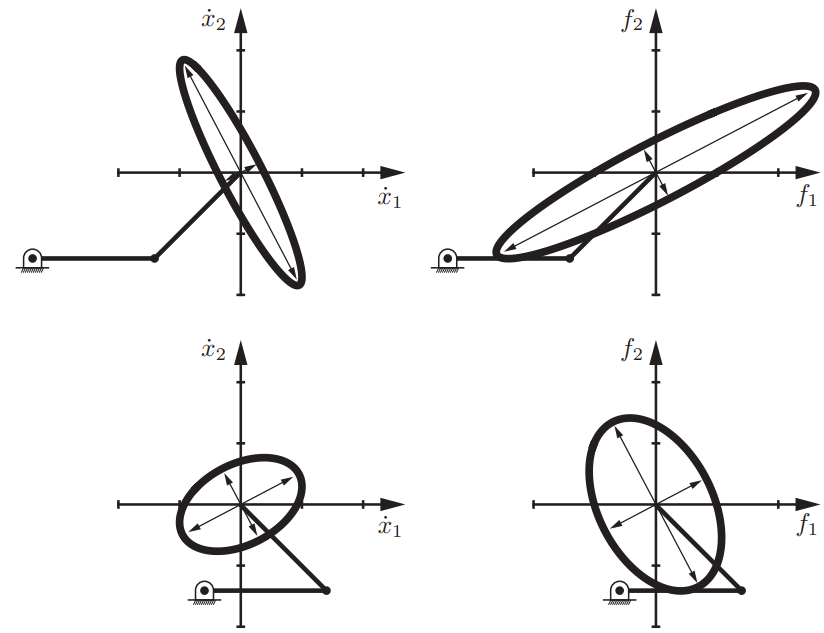
위 그림은 2R 로봇의 두 가지에 congiguration에 대한 조작성 타원체(왼쪽)와 힘 타원체(오른쪽)이다.

이 그림을 보면 알 수 있듯이 타원이 눌린 방향이 서로 반대이다.
더 자세히 설명을 해보자면 조작성 타원체와 힘 타원체의 추축들은 서로 나란하며 각 주축의 길이는 서로에 대해 역수이다.

그럼으로 엔드 이펙터의 속도를 생성하기 쉬운 방향으로는 힘을 생성하기 어렵고 그 반대도 마찬가지라는 것을 알 수 있다.

특이점의 경우에는 조작성 타원체가 선분으로 수렴하여 타원체의 넓이다 0이 되고
힘 타원체는 조작성 타원체가 수렴한 선분에 수직 방향으로 무한히 길어지게 된다.(길어진 방향과 수직인 방향으로는 얇아진다)

이 경우는 팔로 가방을 드는 상황을 예로 들수 있다.
가방을 들때 중력 방향으로 팔을 쭉편 자세가 가장 편한 상태이다.
사람의 팔을 2R로봇팔 이라고 생각 했을 때 이렇게 쭉편 상태가 로봇의 특이점 이며 이 경우 가방의 무게를 관절 구조로만 지탱하는 상황이므로 관절의 토크가 발생할 필요가 없다.

📖속도를 twist로 표현했을 때의 Jacobian

위에서 봤듯이 $v_{tip}$ 은 엔드 이펙터의 좌표를 미분하여 얻기 때문에 엔드 이펙터의 configuration 표현 방법이 $v_{tip}$ 의 형태를 결정하고 이는 Jacobian의 형태까지 결정한다. 우리는 지금까지 로봇의 configuration을 $T\in SE(3)$ 로 표현했고 이 경우 속도를 twist로 표현하였다.
그럼으로 이번에는 $v_{tip}$ 이 twist $\mathcal{V}\in\mathbb{R}^6$ 로 주어지는 경우의 Jacobian을 알아보자

먼저 Jacobian도 표현된 기준 좌표계에 따라 다음과 같이 나뉘어 진다.

twist가 고정 좌표계{s}에서 표현됐을 때 ( $\mathcal{V}_s$ = $J_s(\theta)$ $\dot\theta$ ): space Jacobian
twist가 물체 좌표계{b}에서 표현됐을 때 ( $\mathcal{V}_b$ = $J_b(\theta)$ $\dot\theta$ ) : body Jacobian

📌Space Jacobian

space jacobian부터 알아보자
n-link open chain 로봇의 forward kinematics을 PoE방법으로 다음과 같이 표현해보자

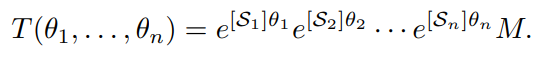
이 때 spatial twist $\mathcal{V}_s$ 는 $[\mathcal{V}_s]$ $=\dot{T}T^{-1}$ 을 이용하여 구할 수 있다.

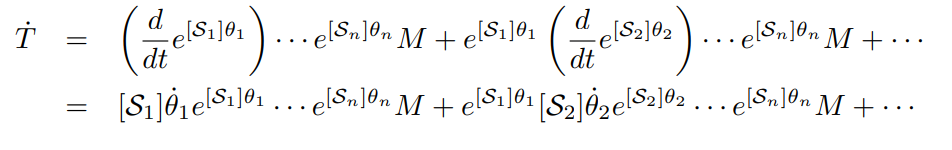
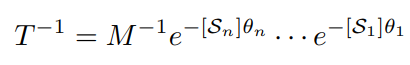
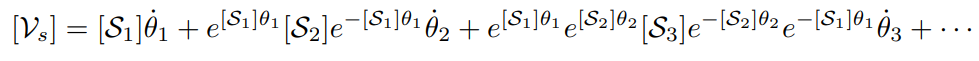
이 식을 벡터 형태로 변환하면 다음과 같이 쓸 수 있다.

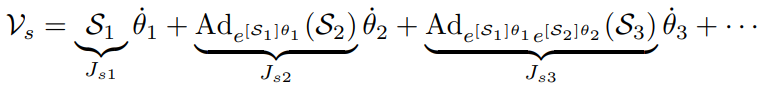
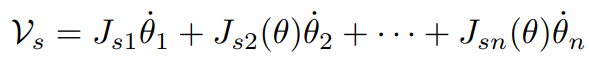
행렬 형태로 변환하면

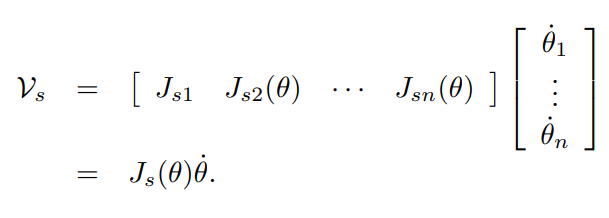
space jacobian $J_s$ 를 볼 수 있다.

위 유도 과정에서 볼 수 있듯이 $J_s$ 의 i번째 열은 다음과 같다.

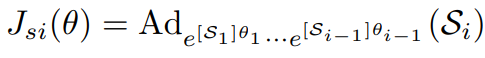
$J_{s1}=\mathcal{S}_1$ 이고 $J_{si}=AD_{T^{i-1}}\mathcal{S}_i$ 로 표현할 수 있으며
즉 $J_{si}$ 는 zero position이 아닌 임의의 로봇 configuration에서 i번째 관절의 screw축(고정 좌표계에서 표현된)을 의미한다.

다음은 RRPRRR로봇의 space jacobian을 구하는 과정이다.

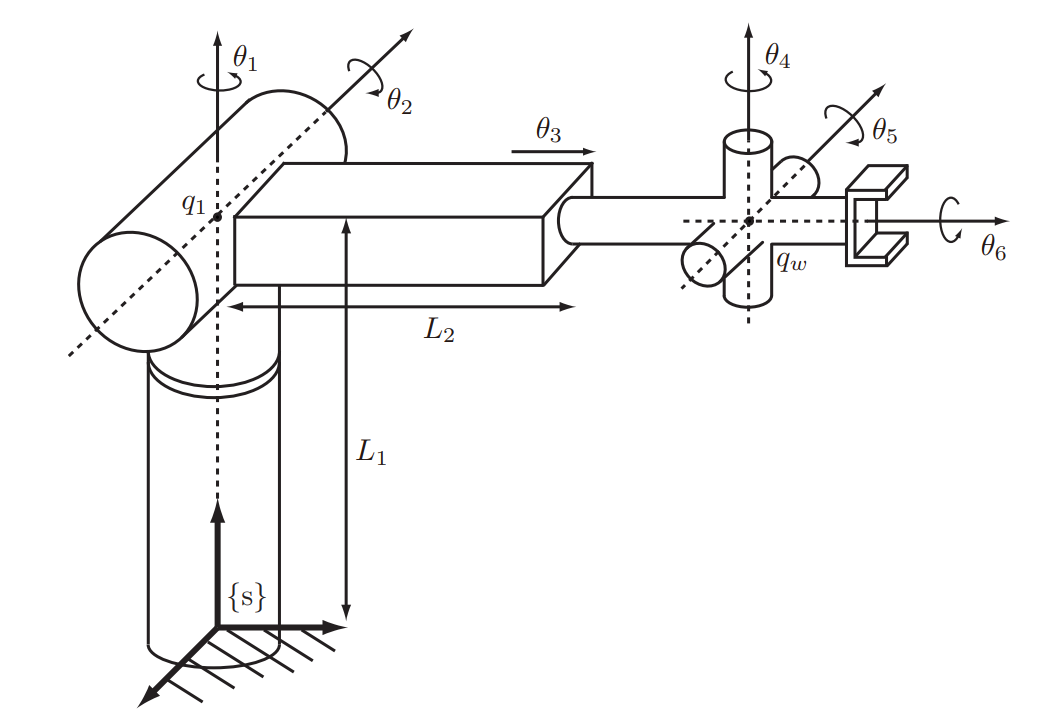
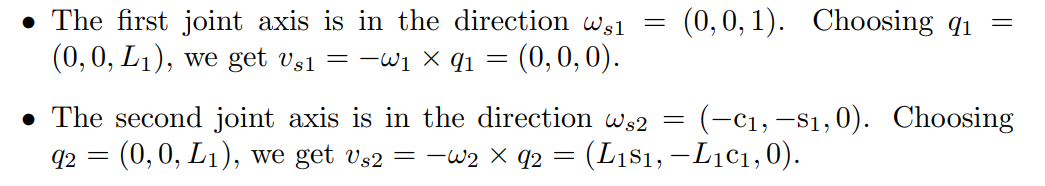
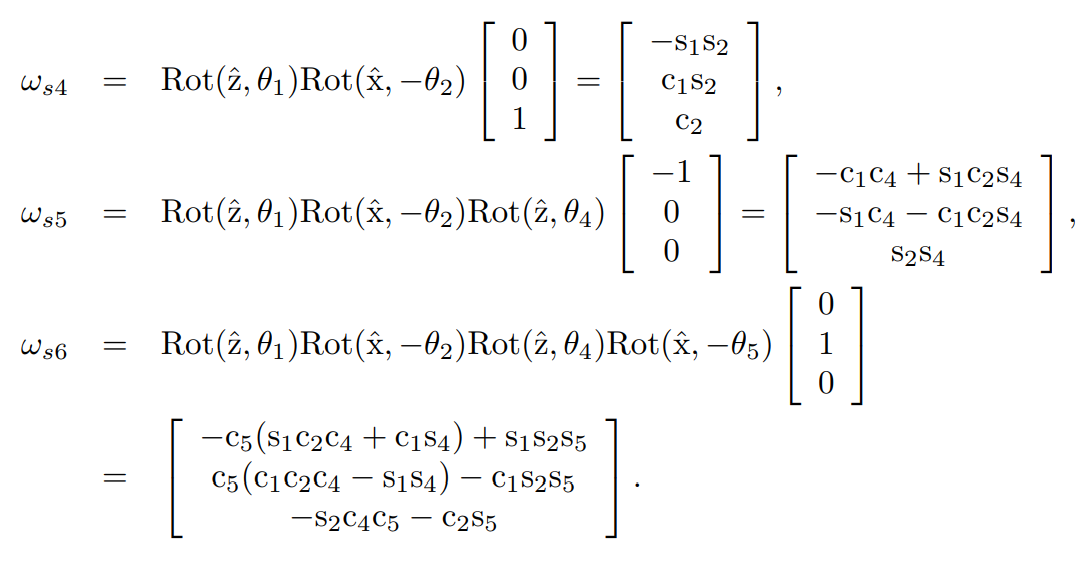
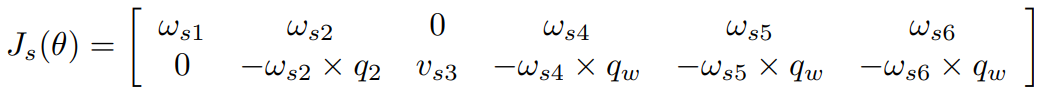
📌Body Jacobian

n-link open chain 로봇의 forward kinematics를 다음과 같이 표현하고

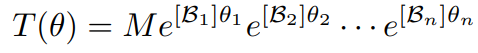
이번에는 body twist $\mathcal{V}_b$ 를 구하는 식을 세워보자
$[\mathcal{V}_b]$ $=T^{-1}\dot{T}$ 을 이용하여 구할 수 있다.

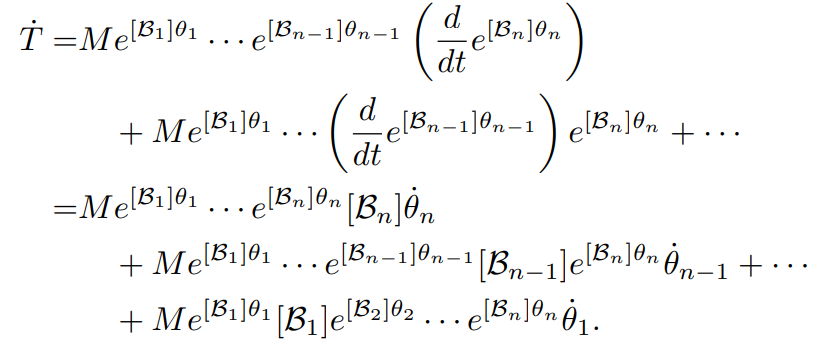
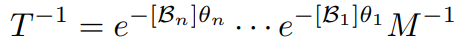
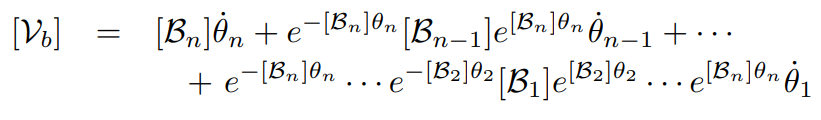
벡터 형태로 변환하면

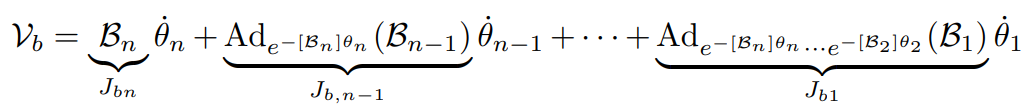
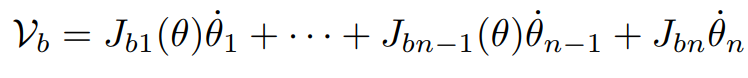
행렬 형태로 변환하면

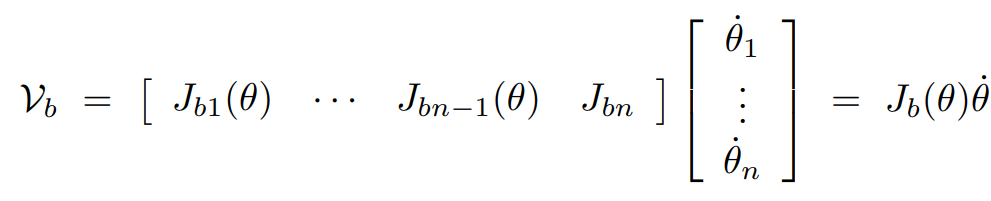
body jacobian $J_b$ 를 볼 수 있다.

$J_{bn}=\mathcal{B}_n$ 이며 $J_b$ 의 i번째 열은 다음과 같으며

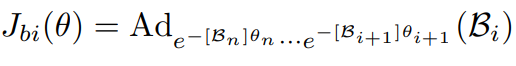
임의의 configuration에서 엔드 이펙터 좌표계에서 표현한 i번째 관절의 스크류 축이다.

아래 그림을 통하여 space jacobian, body jacobian을 직관적으로 이해할 수 있다.

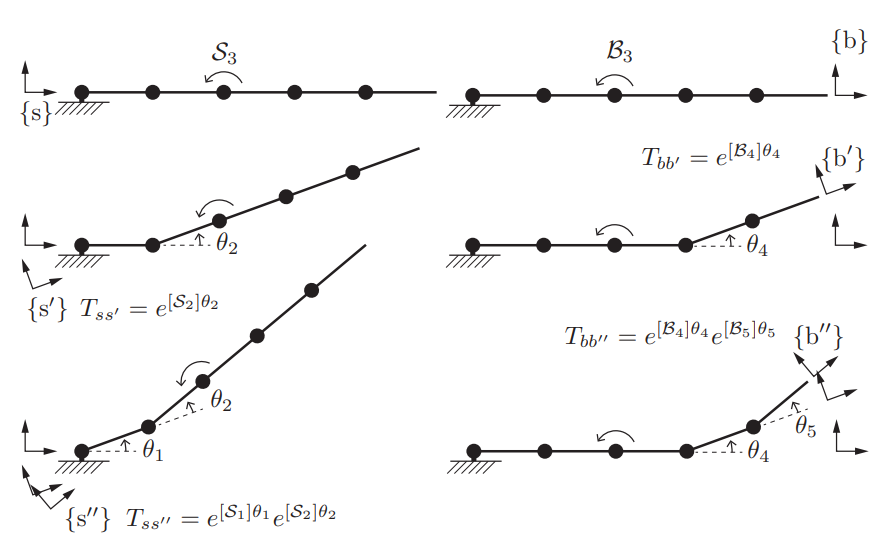
📌 Space Jacobian과 Body Jacobian의 관계

Jacobian의 열 벡터는 twist이기 때문에 twist때와 같이 Jacobian도 adjoint map을 사용하여 기준 좌표계를 바꿀 수 있다.

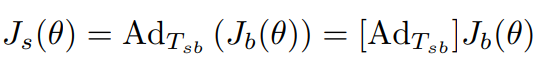
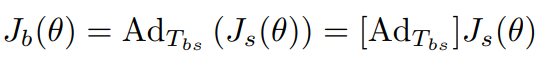
여기서 $T_{sb}$ 는 로봇의 forward kinamatics이다.

📖Jacobian의 다른 표현(analytic Jacobian)

위에서 봤듯이 엔드 이펙터의 configuration 표현법에 따라 Jacobian의 형태가 결정된다.
이번에는 $T\in SE(3)$ 가 아닌 최소한의 좌표 집합 $q$ 를 사용하여 엔드 이펙터를 표현하는 경우를 다뤄 볼 것이다.
3차원 task space경우에 보통 $q\in\mathbb{R}^6$ 는 엔드 이펙터 원점의 위치를 표현하는 3개의 좌표와 엔드 이펙터의 방향을 나타내는 3개의 좌표로 구성되며
3개의 좌표로 방향을 표현할 때 오일러 회전각,혹은 지수좌표를 사용한다.
이때 모두 고정 좌표계에서 표현된다.

엔드 이펙터의 속도는 $q$ 를 시간에 대해 미분한 $\dot{q}$ 이며 Jacobian을 통해 표현하면 $\dot{q}$ $=$ $J_a(\theta)$ $\dot\theta$ 이며 $J_a(\theta)$ 를 analytic Jacobian이라고 부른다.

$q\in\mathbb{R}^6$ 에서 지수 좌표 $r=\hat{w}\theta$ 를 사용하여 방향을 표현한다고 했을 때
다음과 같이 analytic Jacobian을 body Jacobian을 통해 구할 수 있다.

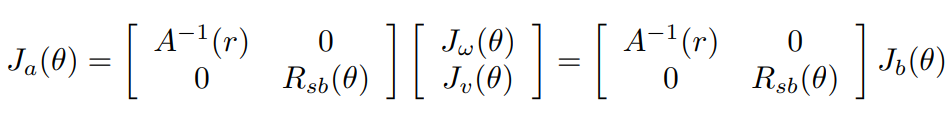
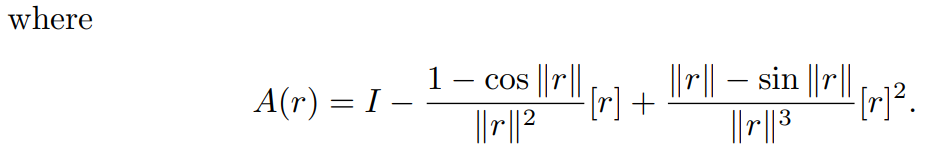
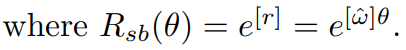
📖Inverse Velocity Kinematics 맛보기

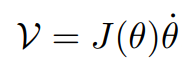
Jacobian을 이용하여 관절의 속도가 주어졌을 때 엔드 이펙터의 속도를 구할 수 있었다.
이번에는 엔드 이펙터의 속도가 주어졌을 때 필요한 관절의 속도를 구해보자

Jacobian의 역행렬이 존재한다면 다음과 같이 $\dot\theta$ 을 쉽게 구할 수 있다.

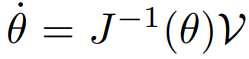
로봇의 관절의 개수 n이 twist 원소 개수인 6과 같고 full rank 일때만 Jacobian의 역행렬이 존재하며 $n\ne 6$ 일 때는 다음과 같은 해석이 가능하다.

$n<6$ 일 때 관절의 수가 부족하여 발생시킬수 없는 twist가 존재한다.
$n>6$ 일 때 관절의 개수가 많기 때문에 더 다양한 움직임을 구현할 수 있고 이러한 경우를 robot redundant라고 부른다. 이때 정해진 twist는 관절 속도에 6개의 제한을 걸게 되고 남은 $(n-6)$ 개의 자유도는 로봇 내부 운동을 발생시킨다.
(예를 들어 사람의 팔을 7R로봇 봐보자 책상위에 손바닥을 고정시킨 상태에서 팔꿈치를 1자유도 만큼 움직일 수 있다.)

📖Open Chains의 정역학

📖 Jacobian을 사용한 정역학

로봇이 정적평행이고 엔드 이펙터에 wrench $-\mathcal{F}$ 가 작용될 때 이 힘을 버티기 위한 관절의 토크를 구할 수 있다.

Untitled

유도 open chain robot에서 에너지 보존 법칙을 다음과 같이 표현할 수 있다.

(관절의 일률) = (로봇을 움직이기 위해 필요한 일률) + (엔드 이펙터의 일률)

정적평형상태를 가정하면 로봇의 알짜힘이 0이기 때문에 다음과 같다

(관절의 일률) = (엔드 이펙터의 일률)

이것을 식으로 나타내면 이 식은 고정, 물체 좌표계에 모두 적용되며 Jacobian을 사용하면 다음과 같이 나타낼 수 있다.