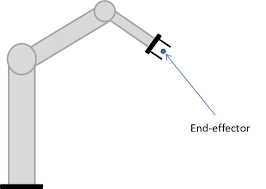
로봇팔에서 로봇의 task는 보통 엔드 이펙터를 통해 이루어 지기 때문에 로봇의 엔드 이펙터의 움직임을 원하는 데로 제어하는 것이 로봇공학의 큰 목표 중 하나이다.
엔드 이펙터는 로봇의 관절 통해 움직이기 때문에 엔드 이펙터와 관절의 움직임 관계를 파악하여야한다.
이 관계를 다루는 학문을 로봇공학에서 기구학이라고 부른다.

이 기구학은 다음과 같이 두 가지로 나뉜다.

• 정기구학(Forward kinematics): 관절의 값을 통해 엔드 이펙터의 위치와 방향을 계산
• 역기구학(inverse kinematics): 엔드 이펙터의 위치와 방향이 주어졌을 때 관절의 값을 계산

이번에는 정기구학에 대해 알아볼 것이다.

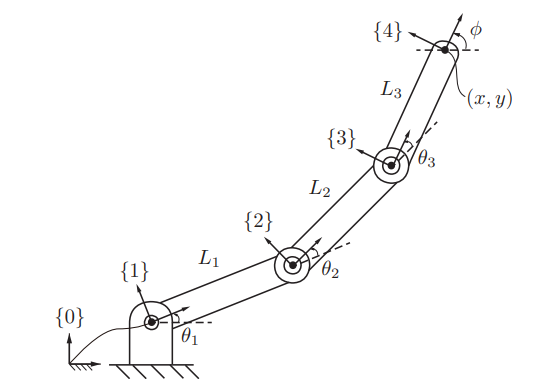
위와 같이 4R(회전형 관절이 4개)로봇이 있고 관절값($\theta$)이 주었졌을 때 엔드 임팩터의 위치(x,y)와 방향($\phi$)을 다음과 삼각함수를 통해 간단히 구할 수 있다.

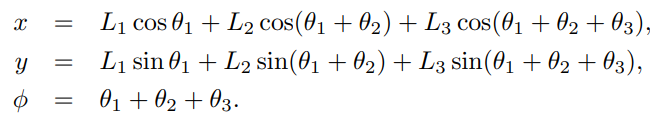
평면상의 로봇에 경우에는 위와 같이 쉽게 구할 수 있지만 로봇이 3차원 운동을 한다면 정기구학적인 분석이 어려워진다. 그래서 우리는 3장에서 배운 강체의 움직임을 통하여 좀 더 체계적으로 정기구학을 구하는 법을 알아볼 것이다.

정기구학을 구하는 방법은 두 가지이다.

• D-H(Denavit-Hartenberg) parameters 를 사용하여 구하기

• PoE(product of exponential: 지수 곱)공식

PoE을 사용하여 정기구학을 구한는 방법을 먼저 알아보자

4.1 Product of Exponentials Formula

PoE공식의 핵심 개념은 모든 관절이 링크에 스크류 운동을 가한다고 가정하는 것이며
보통 고정좌표계{s}와 엔드 이펙터에 부착된 물체 좌표계{b}를 정의하고 {s}에 대한 {b}의 위치와 방향을 스크류 운동 이론을 통하여 구한다.

여기서 고정좌표계와 물체 좌표계 중 어느 좌표계를 기준으로 스크류 운동을 표현하는 지에 따라 정기구학식이 달라진다.

4.1.1 Screw Axes in the Base Frame

먼저 {s}를 기준으로 스크류 운동을 표현했을 때를 알아보자

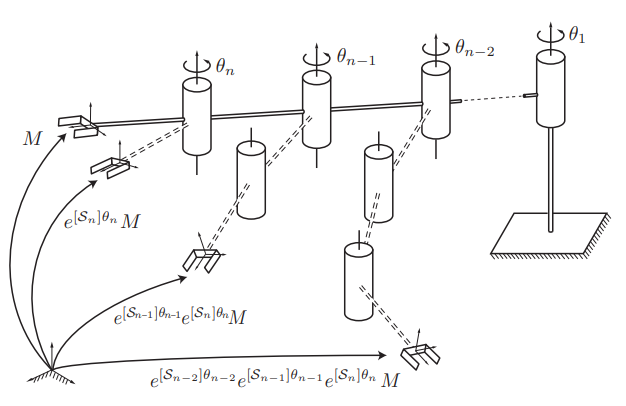
위의 로봇은 회전형 관절이 n개 있는 로봇이다. $i$번째 관절의 회전값을 $\theta_i$이라고 하자
여기서 모든 관절의 값이 0이라고 가정하고 이때의 엔드 이펙트의 위치 즉 {b}를 $M\in SE(3)$이라고한다.
이렇게 로봇이 0인 상태에서 엔드 이펙터와 가까운 관절부터 회전하여 {b}의 위치가 바뀌는 것을 식으로 표현해보자

n번째 관절만 $\theta_n$만큼 회전하고 나머지 관절은 0 위치에 있다고 할때 엔드 이펙터의 위치는 다음과 같다.

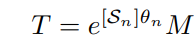
$T\in SE(3)$는 위치가 변한 {b} 즉 엔드 이펙터의 위치와 방향을 나타내고 $S_n\in \mathbb{R}^6$은 로봇의 0 위치에서 n번째 관절의 회전에 대한 스크류 축을 고정 좌표계를 기준으로 표현한 것이다.

$n-1$번째 관절까지 회전한다면 다음과 같다.

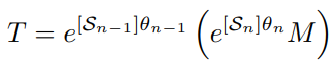
이와 같은 방법으로 엔드 이펙터와 가장 가까운 관절부터 회전하여 모든 관절이 회전하였을 때 엔드 이펙터의 위치와 방향을 다음과 같이 구할 수 있다.

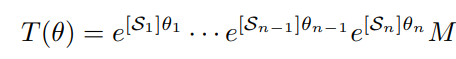
여기서 엔드 이펙터와 가까운 관절부터 회전하는 것은 다음과 같은 이유가 있다.
$(i-1)$번 관절의 회전은 $i$번 관절의 위치를 변화시킨다.(고정 좌표계에서 봤을 때) $S_i$는 0위치에서의 스크류 축 이기 때문에 관절의 위치가 변화되면 $S_i$을 이용하여 운동을 표현할 수가 없다. 그렇기 때문에 $(i-1)$번 관절이 $i$번 관절보다 먼저 회전을 하게되면 나중에 $i$번 관절에 대한 회전운동을 표현할 때 문제가 발생한다. 하지만 $i$번 관절의 회전은 $(i-1)$번 관절의 위치를 변화시키지 않기 때문에 이 때에는 $S_{i-1}$을 그대로 사용할 수 있다. 그렇기 때문에 $i$번이 $(i-1)$번 보다 먼저 회전한다고 가정하고 계산을 하는 것이다.

이렇게 고정좌표계를 기준으로 스크류 운동을 표현하는 PoE를 space form PoE라고 부른다.

4.1.1.1 Examples

가장 많이 사용되는 6R로봇팔의 정기구학을 공간 PoE를 이용하여 구해보자

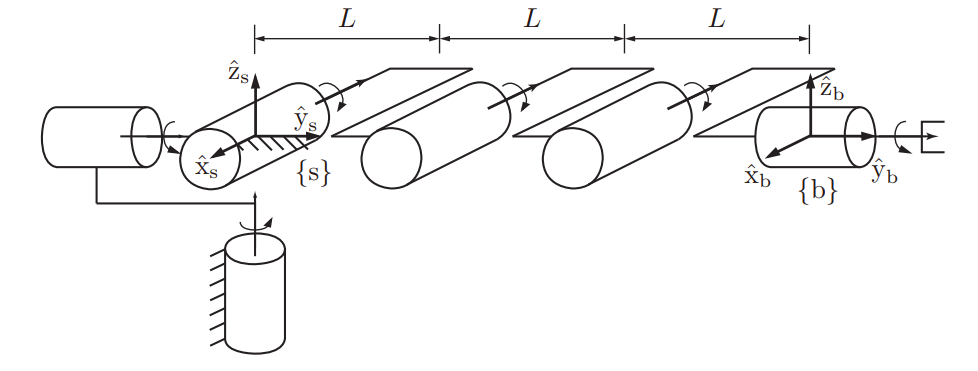
위 그림이 로봇의 0위치라고 할때 $M$을 구해보면 다음과 같다.

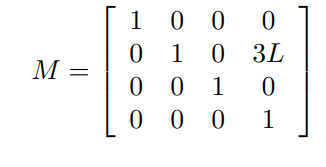
$S_i=(w_i,s_i),i=1...6$은 다음과 같다.

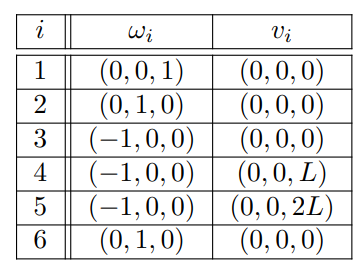
위의 값을 바탕으로 아래에 식에 적용하면 엔드 이펙터의 좌표계를 구할 수 있다.($n=6$)

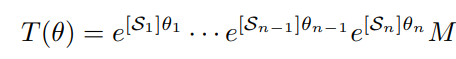
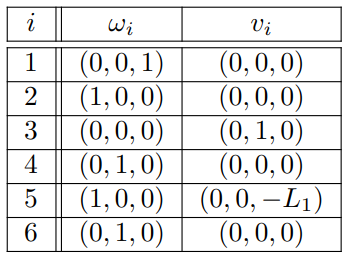
아래 그림처럼 선형관절이 있는 RRPRRR로봇에 경우는 다음과 같다.

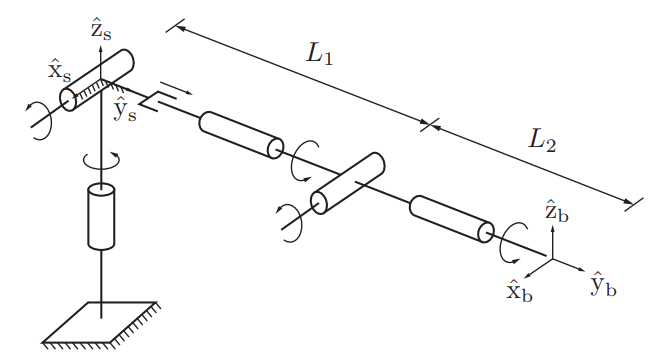
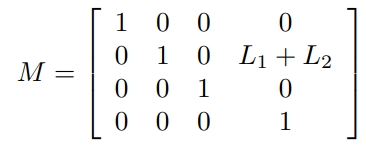
4.1.2 Screw Axes in the End-Effector Frame

엔드 이펙터에 부착된 물체 좌표계{b}를 기준으로 스크류 운동을 표현한 PoE를 body form PoE라고 부른다.

이번에는 body form PoE에 대해 알아보자.

여기서는 다음과 같은 행렬 지수의 성질을 사용하며

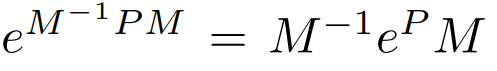
space form 식의 오른쪽 부터 위에 등식을 n번 박복 적용하여 body form 식을 구할 수 있다.

여기서 $[\mathcal{B}_i]=M^{-1}[S_i]M$ 이다.
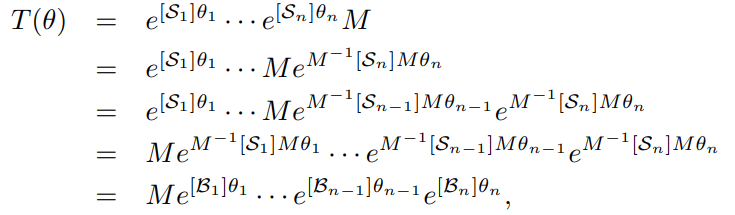
즉 $\mathcal{B}_i=[ADT_{M^{-1}}]S_i$이며 $[\mathcal{B}_i]$는 고정좌표계에서 표현한 스크류 축이라는 것을 알 수 있다. 이 식에서 알 수 있듯이 body form PoE는 엔드 이펙터에서 먼 관절의 스크류 운동부터 고정 좌표계를 기준으로 $M$을 변환시키는 방식으로 계산한다는 것을 알 수 있다.

엔드 이펙터에서 먼 관절부터 적용하는 이유는 space form의 경우와 반대이다.
엔드 이펙터의 좌표계에서 봤을 때는 $i$번 관절의 운동은 $(i-1)$번 관절의 위치를 변화시지만. $(i-1)$번 관절의 회전은 $i$번 관절의 위치를 변화시키지 않기 때문이다.

4.1.2.1 Examples

앞에서 다룬 6R로봇을 이번에는 body form PoE를 이용하여 구해보자

$M$은 space form 일 때와 똑같다.

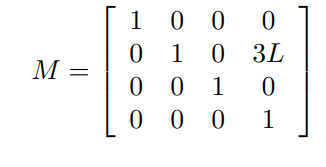
이번에는 인데 이펙터 기준 좌표계를 기준으로 각 관절 운동의 스크류 축 $\mathcal{B}_i=(w_i,v_i)$을 정리해보자

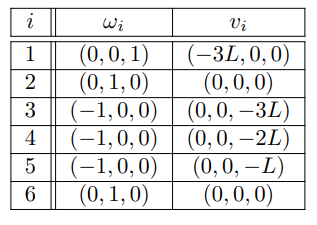
이 정보를 바탕으로 다음과 같이 계산하여 엔드 이펙터의 좌표를 알 수 있다.

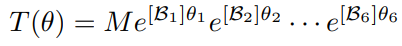
4.2 Denavit–Hartenberg Parameters

D-H parameters 방법
나중에 작성 예정이다.

4.3 The Universal Robot Description Format

정기구학에서 중요하게 다룰 파트는 아니라고 생각하지만
modern robotics 책에서는 설명하기 때문에 간단하게 언급만 하겠다.

Universal Robot Description Format 번역하면 로봇 기술용 통일 포멧이며
줄여서 URDF라고 불린다.
URDF는 로봇의 동작을 구현하기 위해 필요한 각 링크들의 지오메트리, 질량 등의 정보가 있는 xml 파일이다. 즉 URDF파일이 있으면 여러 시뮬레이션 툴에서 그 로봇의 동작 제어를 구현해 볼 수 있다. ROS(Robot Operating System)에서 주로 사용된다.