동적 계획법(DP, Dynamic Programming)

문제에 대한 정답이 될 가능성이 있는 모든 해결책을 체계적이고 효율적으로 탐색하는 풀이법이다

모든 해결책을 다 탐색해보는 완전 탐색은 기본적으로 높은 시간 복잡도를 가진다. 이를 체계적이고 효율적으로 탐색하기 위해서는 몇 가지 조건이 있어야 한다.

• Overlapping Subproblems - 중복 하위 문제
  • 중복 계산해야 하는 하위 문제가 존재한다.
• Optimal Substructure - 최적 구분 구조
  • 하위 문제에서 구한 최적의 답이 큰 문제의 최적의 답을 구할 수 있는 구조여야 한다.

---

피보나치 수열을 통한 DP의 개념

function fibo(n) {
    if (n === 1 || n === 2) {
        return 1;
    }
    return fibo(n - 1) + fibo(n - 2);
}

위 코드의 시간복잡도는 매 번 2개의 함수를 호출하여 O(2ⁿ)이다. 그러나 이 코드에서는 중복 하위 문제들이 존재한다.

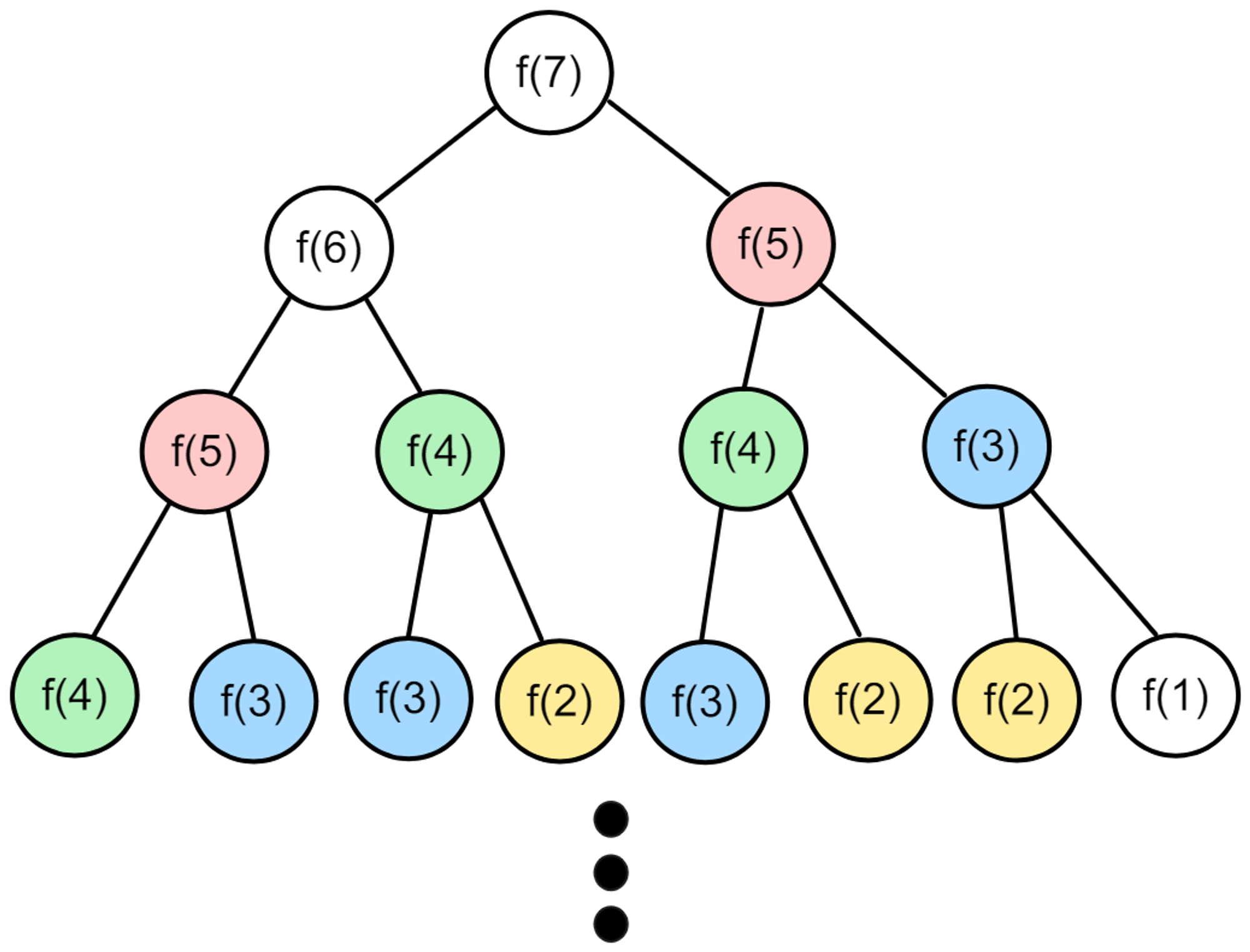
위 사진과 같이 상당한 중복이 발생하는 것을 볼 수 있다. f(5)를 전에 계산했다면 후에 같은 과정으로 f(5)를 계산 할 필요가 없는 것이다. 만약 계산하지 않을 시에 시간복잡도는 O(n)으로 줄게 된다.

---

Top-down 방식

아래와 같은 방식은 f(n)부터 f(1)로 접근하며 memo를 채워 나가는 것을 memoization이라고 한다.

let memo = {};
function fibo(n) {
    if (n === 1 || n === 2) {
        return 1;
    }
    if (!(n in memo)) {
        memo[n] = fibo(n - 1) + fibo(n - 2);
    }
    return memo[n];
}

---

Bottom-up 방식

아래와 같은 방식은 f(1)부터 f(n)로 접근하며 memo를 채워 나가는 것을 tabulation이라고 한다.

let memo = {};

function fibo(n) {
    for (let i = 3; i <= n; i++) {
        memo[i] = memo[i - 1] + memo[i - 2];
    }
    return memo[n];
}

---

💡 Top-down 방식은 재귀로 구현되고, Bottom-up 방식은 반복문을 통해 구현된다!