선형회귀(Linear regression)
선형회귀 분석이란 관찰된 데이터들을 기반으로 하나의 함수를 구해서 관찰되지 않은 데이터의 값을 예측하는 것을 의미합니다.
- 영향을 받는 변수를 종속변수 혹은 반응변수라고 하고 보통 y로 표기합니다.
- 영향을 주는 변수를 독립변수 혹은 설명변수라 하고 보통 x,x1,x2등으로 표기합니다.
단순선형회귀모형
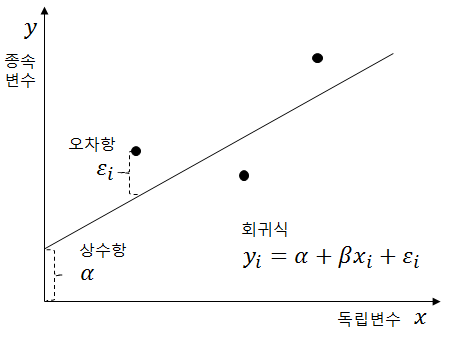
출처 - https://analytics17.blogspot.com/2017/08/2-1.html
- 한 개의 독립변수와 하나의 종속변수로 이루어져 있는 모델입니다.
- 위의 모형이서 b0과 b1은 회귀계수라고 합니다. b1은 독립변수 x1의 회귀계수입니다.
- e(엡실론)은 오차항으로 보통의 평균이 0이고 분산이 오메가 제곱인 정규모형을 따른다고 가정합니다.
- 회귀계수의 추정치는 보통 제곱오차를 최소로 하는 값으로 구합니다.
단순선형회귀모형이 종속변수를 잘 설명하는데 충분하지 않으면 두 개 이상의 독립변수를 사용하여 종속변수의 변화를 설명하는 다중회귀분석(중회귀분석)을 실시할 수 있습니다.
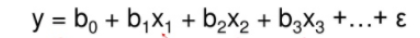
적합한 모형을 찾은 후에는 적절한지 확인을 해야합니다.
- 모형이 통계적으로 유의미한가?
- F통계랑을 확인한다. 유의수준 5% 하에서 F통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있습니다.
- 회귀계수들이 유이미한가?
- 해당 계수의 t통계량과 p-값 또는 이들의 신뢰구간을 확인해야 합니다.
- 모형이 얼마나 설명력을 갖는가?
- 결정계수를 확인해야 합니다.. 결정계수는 0에서 1값을 가지며, 높은 값을 가질수록 추정된 회귀식의 설명력이 높습니다.
- 모형이 데이터를 작 적합하고 있는가?
- 잔차를 그래프로 그리고 회귀진단을 해야합니다.
- 아래 다섯가지 가정을 만족시키는가?
- 선형성 → 독립변수에 변화에 따라 종속변수도 일정 크기로 변화
- 독립성(잔차와 독립변수의 값이 관련돼 있지 않음)
- 등분산성(독립변수의 모든 값에 대해 오차들의 분산이 일정)
- 비상관성(관측지들의 잔차들끼리 상관이 없어야 함)
- 정상성(잔차항이 정규분포를 이뤄야 함)

경사하강법
회귀 모델을 구현할 때 최초 회귀 계수를 임의값으로 설정한 후, 경사하강법을 반복적으로 실행해 최소의 평균 제곱 오차를 가지는 회귀 계수를 구합니다.
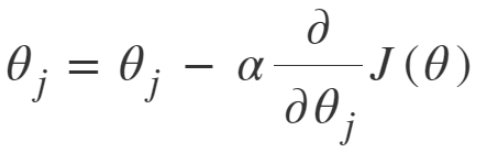
위 공식을 설명하면, 어느 한 지접에서 J(세타)의 미분값과 반대대는 방향으로 세타를 조금 움직여, 결과적으로 J(세타)의 값이 줄어들게 만드는 공식입니다. 이 경사하강법을 반복적으로 수행하면 결과적으로 J(세타)를 최소로 하는 세타를 구하게 됩니다.
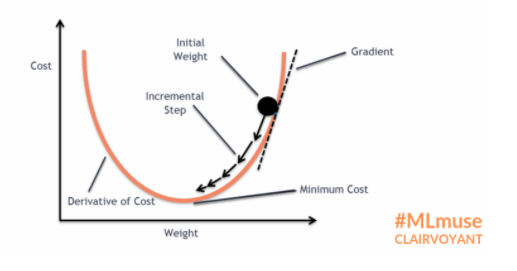
코스트가 가장 낮은 점에서의 값을 구하기 위해서 반복적으로 특정 지점에서의 기울기를 구하고 기울기의 반대 방향으로 가중치를 조절하며 최적의 값을 찾습니다.
#데이터 생성
X = np.linspace(0, 10, 10)
Y = X + np.random.randn(*X.shape)
for x, y in zip(X,Y):
print((round(x,1), round(y,1)))
#모델 생성
model = Sequential()
model.add(Dense(input_dim=1, units=1, activation="linear", use_bias=False))
#경사하강법으로 평균제곱오차(MSE)줄이기
sgd = optimizers.SGD(lr=0.05) #lr은 학습률을 0.05로 설정하는 것을 의미
#lr 이 너무 작을경우 학습속도가 느리고 너무 클 경우 학습이 잘 안됨
model.compile(optimizer='sgd', loss='mse')
#가중치 보기
weights= model.layers[0].get_weights()
weights
#학습
model.fit(X,Y, batch_size=10,epochs=10,verbose=1)
#가중치 확인
weights = model.layers[0].get_weights()
w = weights[0][0][0]
#시각화
plt.plot(X,Y,label='data')
plt.plot(X, w+X, label="regression")
plt.legend()
plt.show()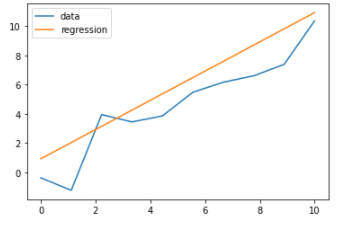
출처 - 나의 첫 머신러닝/딥러닝, 데이터 분석 전문가 가이드
