Lecture 6 는 두차례에 걸쳐 Neural network에 대해 배우게 된다.
Activation Function
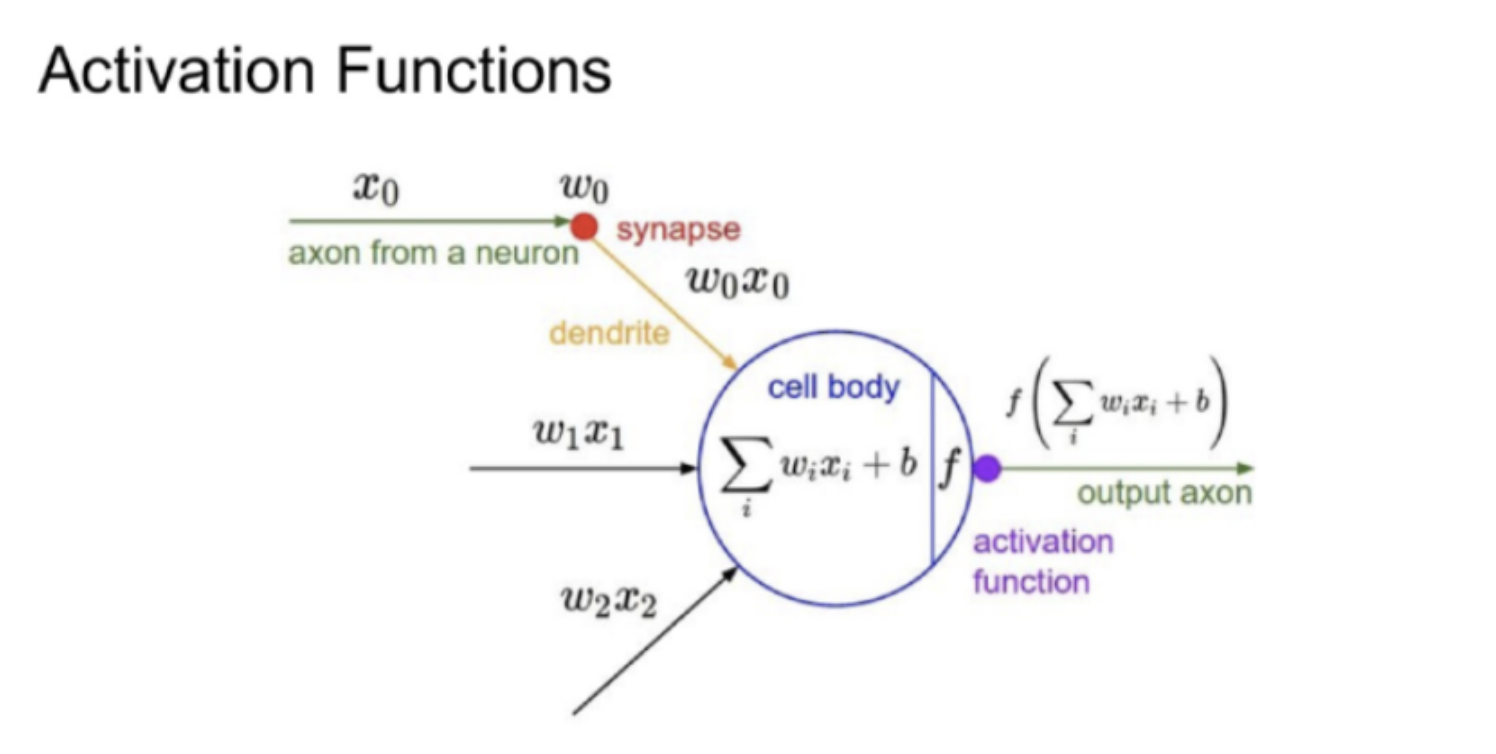
입력값이 들어오면 cell body를 non-linear하게 만들어 준다.non-linear하게 만들어주는 것은 non-linear한 문제들을 해결하기 위해 중요한 부분으로 알고있다.

최근에는 GELU라는 NLP에서 인기있는 activation function을 배운 기억도 있다.
중요하게 알아야 할 function들이고 각 function의 장단점을 배웠다.
Sigmoid

sigmoid function은 넓은 범위안의 수들을 0과 1사이 값으로 바꾸어준다.
몇가지 문제가 있어서 더 이상 사용하지 않는다고 생각할 수 있다.
-
Neuron saturated into one or zero (vanishing gradient)
input이 너무 크거나 작으면 0에 가까워진다. 그럼 gradient가 소멸하게 된다.
back prop시 dL/dw 가 0이 되므로 w의 업데이트가 없어지는 saturated regine이 나타난다. -
Not zero-centered -> zigzag path
sigmoid의 값은 항상 positive num으로 나오게 된다. 이때 w의 없데이트는 항상 같은 부호로만 업데이트되며 같은 방향으로만 움직이게 된다. 그래서 optimal 한 경우보다 비효율 적으로 움직이게 되는데 지그재그 형태가 나타나며 zigzag path라고 한다. -
exp() is too expensive
exp연산이 너무 비싸다. 오래걸리므로 효율x
tanh

tanh는 sigmoid에 비해 zero centered되어 있어 zigzag path 문제를 해결한 점에서 좋다.
하지만 kill gradient 문제를 해결하지는 못했다.
ReLU
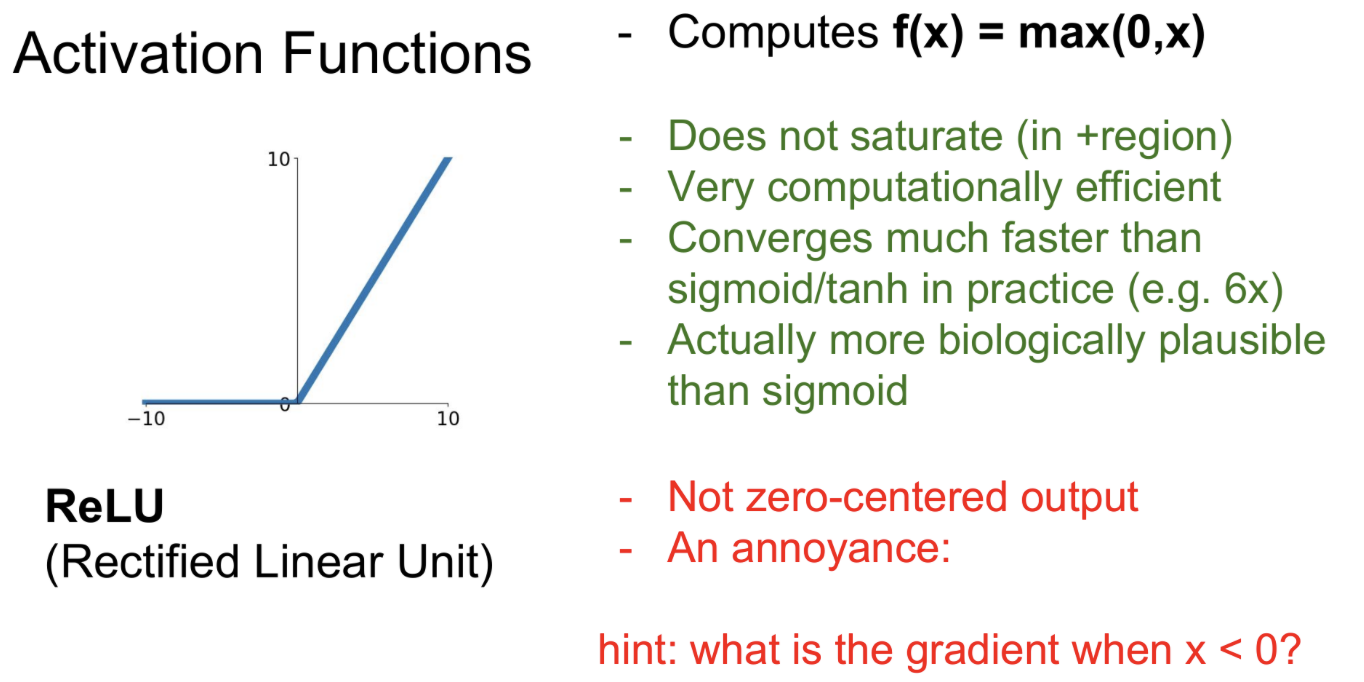
내가 딥러닝 공부 이후 가장 많이 본 activation function이다.
장점이 정말 많다.
1. not saturate
2. computationally efficient -> exp같은 비산 연산 x
3. converges faster
4. biologically plausible
단점은 다음과 같다.
- not zero-centered
- An annoyance -> 0보다 작은 음수 데이터는 kill gradient 현상이 일어남. nitialization에서 운이 좋지 않은 몇개의 neuron들은 gradient가 update가 되지 않음
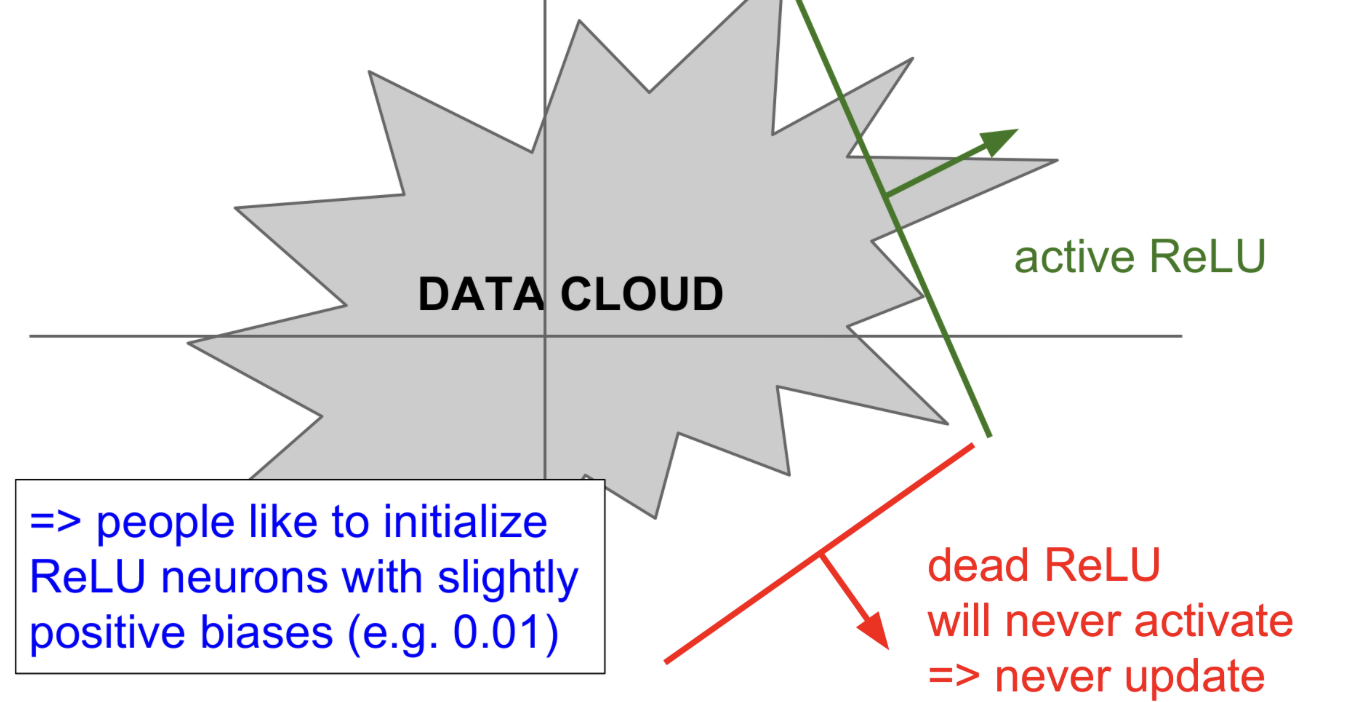
Dead ReLU를 막기 위해 약간의 positive 값으로 bias를 초기화하는 시도도 있었다.
Leaky ReLU and PReLU

Dead ReLU를 막기 위해 고안되었다. PReLU의 å값이 0.01로 하드코딩한 것이 LeakyReLU이다. 실제 PReLU는 Back prop을 진행하며 상황에 따라 å값을 선택한다.
ELU

ReLU의 장점을 갖고있다.
출력의 평균이 0에 가까워지기 때문에, bias shift가 감소하여 gradient 소실 문제를 줄여준다.
ReLU와 Leaky ReLU의 중간 형태인데 x가 0보다 작은 영역에서 약간의 saturation을 허용하는 것(neuron(gradient)이 죽는 것)이 noise에 조금 더 robust 하다는 주장이다.
exp()연산을 하는 단점이 있다.
Maxout

ReLU와 Leaky ReLU를 일반화한 상태이다.-> 두개의 linear function을 max를 찍는 형태이다.
죽는 현상은 안나타나지만 parameter가 두배가 된다.
Data Preprocessing
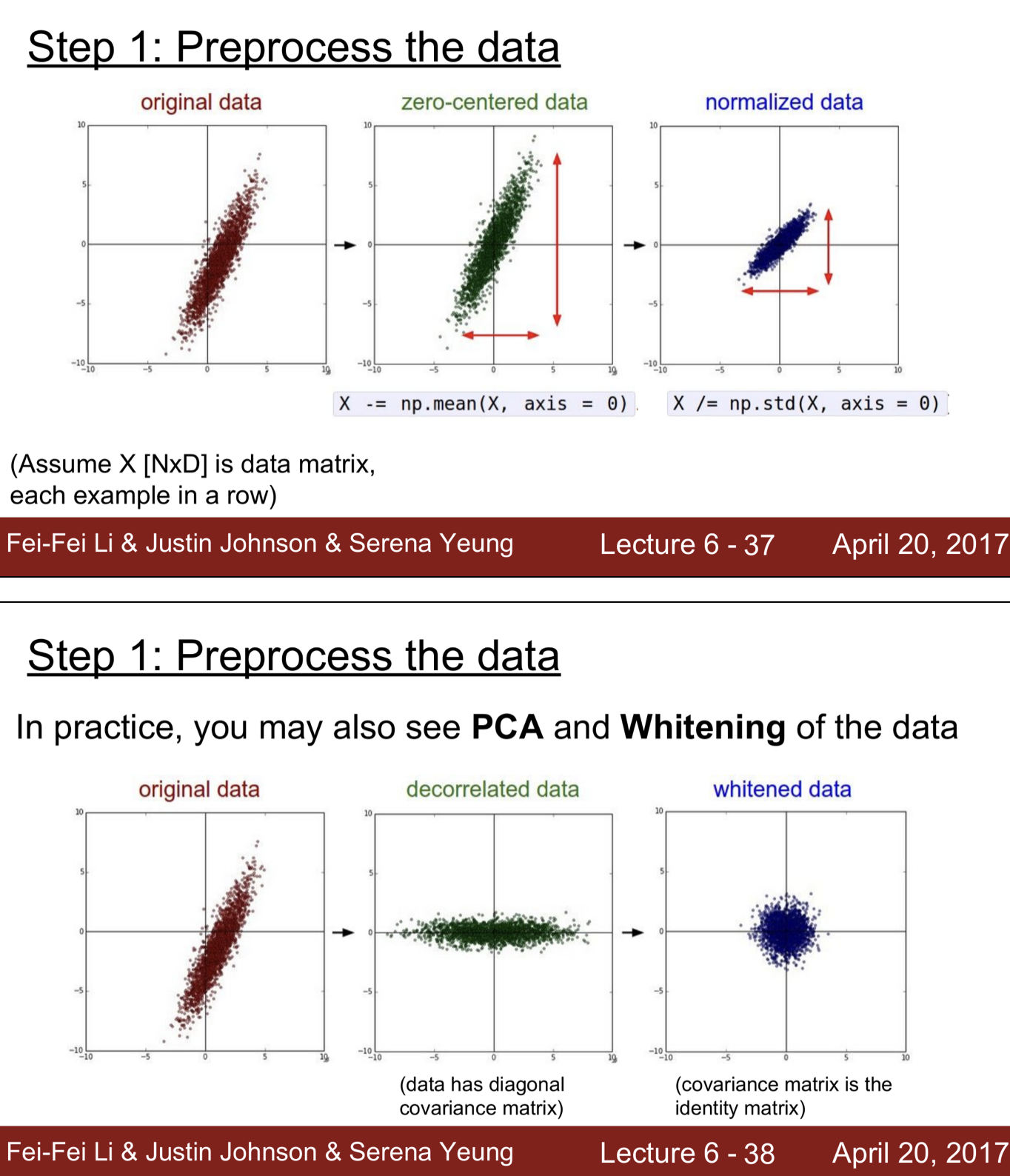
zero-centered, nomalized, PCA, whitened 등이 있다.
이미지에서는 각 위치에서 픽셀들이 상대적으로 비슷한 규모와 분포를 가지므로, 머신러닝에서보다 더 많은 normalization을 수행할 필요는 없다.
일반적으로는 zero mean을 수행하고, 다른 기법은 사용하지 않는다.
- 전체 이미지 평균이나 채널(RGB)별 평균을 빼는 방법 등을 사용
- 엄밀하게 따지자면, 첫번째 layer의 input에서만 zero mean이 되고, 네트워크가 깊어지면서 데이터는 zero mean이 되지 않음
Weight Initialization
weight initialization은 굉장히 신중함이 필용한 작업이다.
모두 0으로 초기화시 input에 대해서 모두 같은 것을 출력하기 때문에 모두 같은 gradient를 얻게 되고, 이 때문에 모두 같은 방식으로 update가 되며, 모든 neuron이 같아지게 되는 문제가 있다. -> Symmtric Breaking
Weight Initialization에 대해 실험을 진행한다.
작은 random num으로 Initialization

random num에 0.01을(Gaussian distribution, standard deviation = 0.01 ) 곱해서 weight initialization을 진행한다.
결과는 얕은 network는 괜찮지만 deap network에서는 문제가 생긴다.
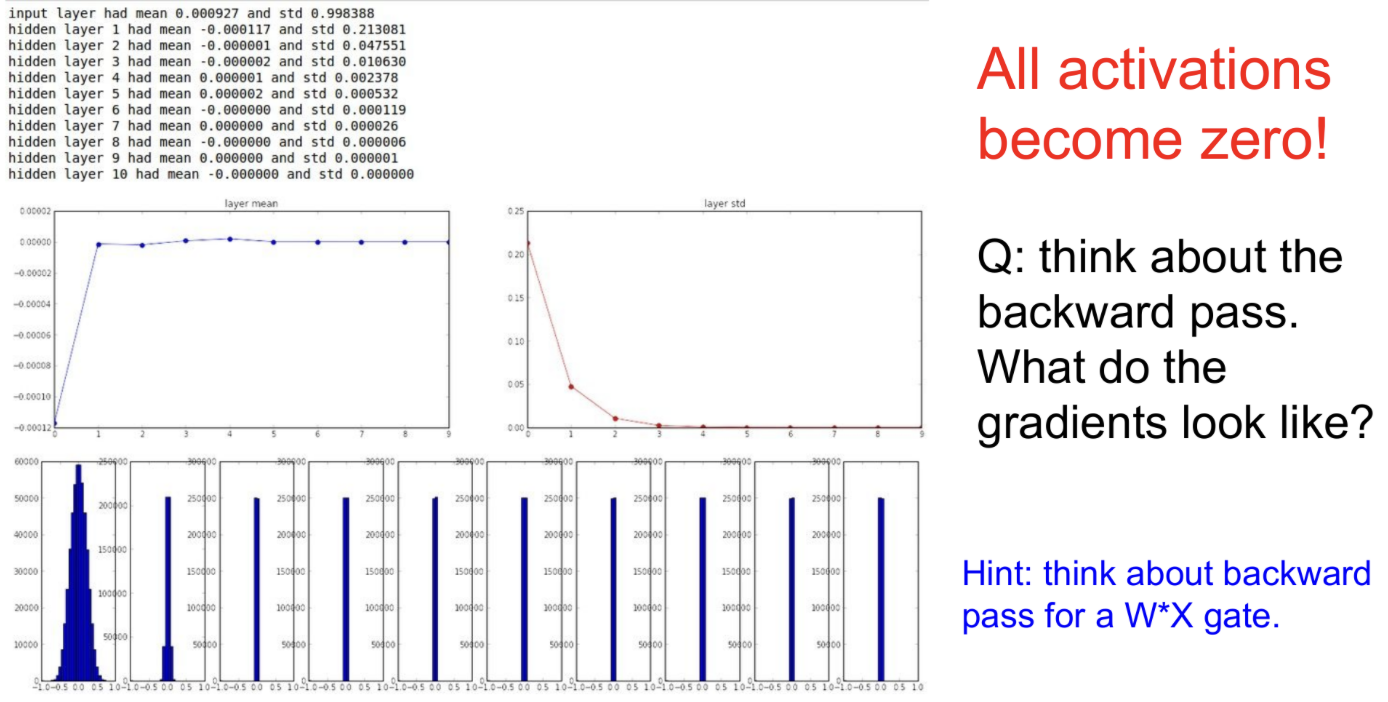
In Forward:
작은 W값들을 계속해서 곱하면서 이 값들이 매우 빠르게 작아지기 때문에 Activaiton이 0이 된다.
In Backward
작은 W값으로 인해 input x가 매우 작다.
따라서, local gradient dW/df = x도 작아지고, 결국 가중치는 아주 작은 gradient를 얻게 되어 update가 일어나지 않게 된다.
큰 random num으로 Initialization
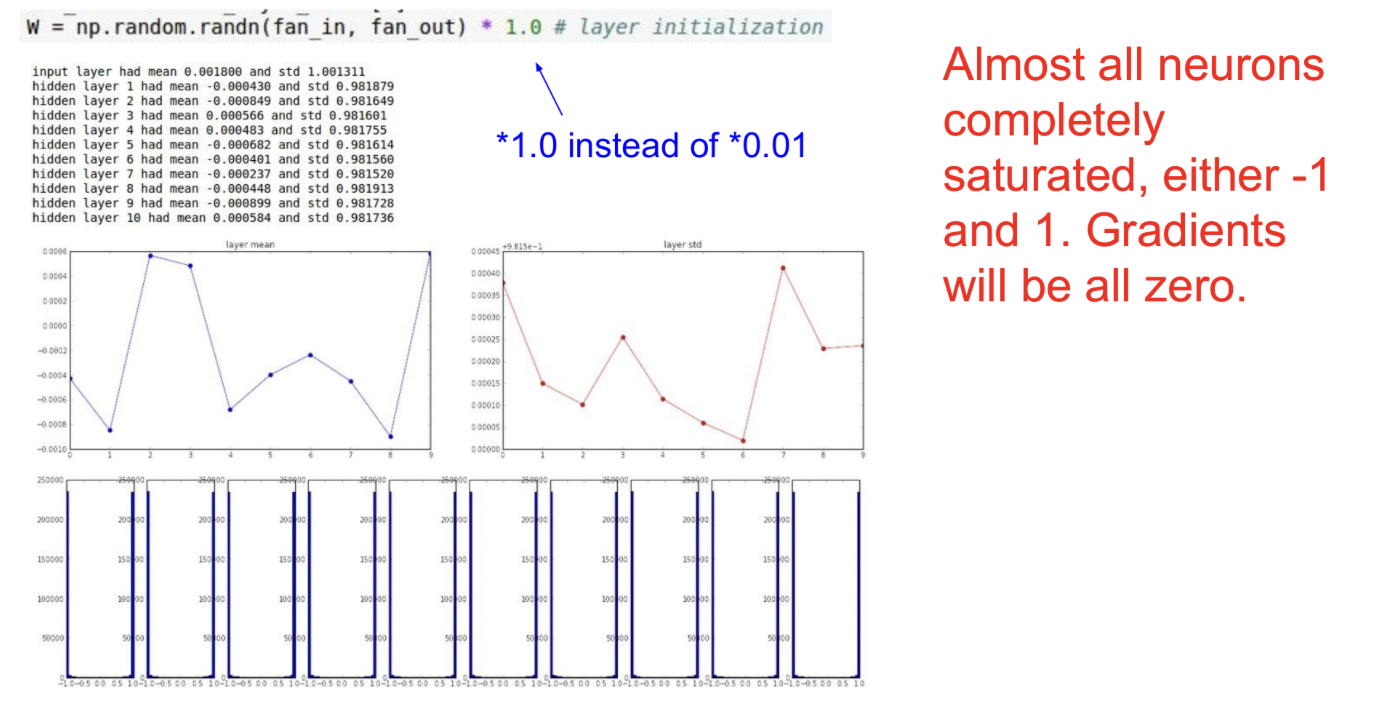
random num에 1을(Gaussian distribution, standard deviation = 1 ) 곱해서 weight initialization을 진행한다.
W가 1또는 -1에 수렴하게 된다.
따라서, gradient가 0이되고, update가 일어나지 않는다.
Solution: Xavier Initialization
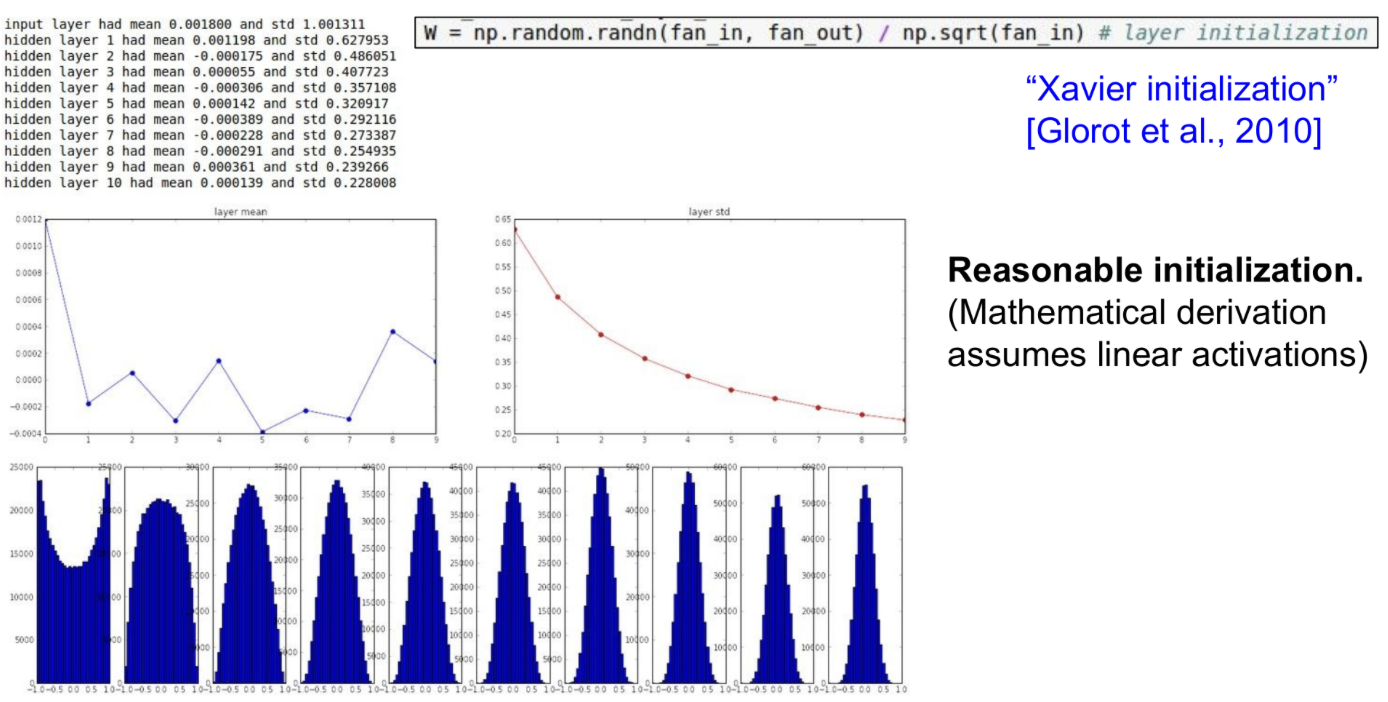
위의 두 상황 다 문제가 있다. 적절한 값으로 initialize 가 중요하다.
Xavier Initialization은 입력과 출력의 분산이 동일하도록 하는 초기화 방법이다.
입력이 작다면 더 작은 수로 나누게 되고, 더 큰 weight를 얻게 됨
-> 작은 입력과 큰 weight를 곱하므로, 적절한 값이 나오게 된다.
입력이 크다면 더 큰 수로 나누게 되고, 더 작은 weight를 얻게 됨
-> 큰 입력과 작은 weight를 곱하므로, 적절한 값이 나오게 된다.
ReLU에서 Xavier Initialization
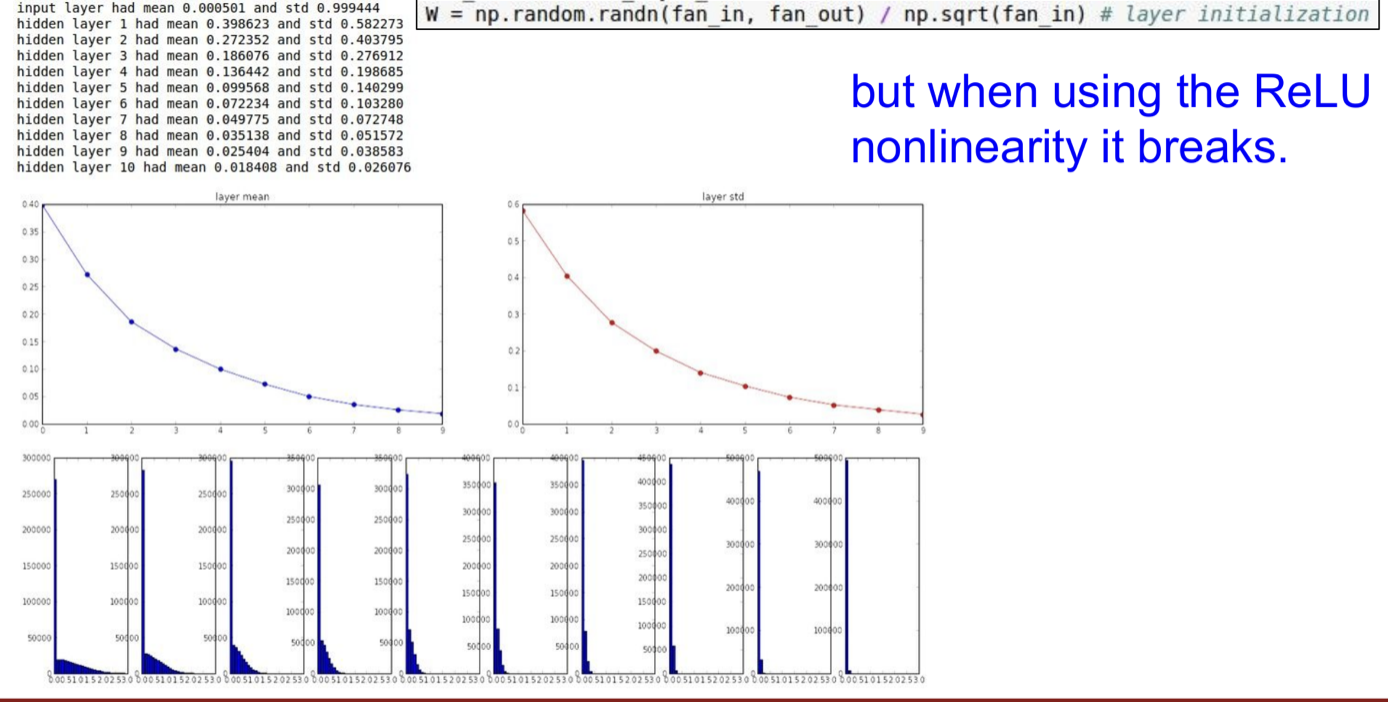
ReLU는 절반의 unit을 죽이기 때문에 Xavier를 사용해서 얻은 분산의 절반이 없어지게 된다.
-> 출력의 분포가 점점 줄어들게 되므로 ReLU에서는 Xavier가 적절하지 않다.
Solution : He Initialization
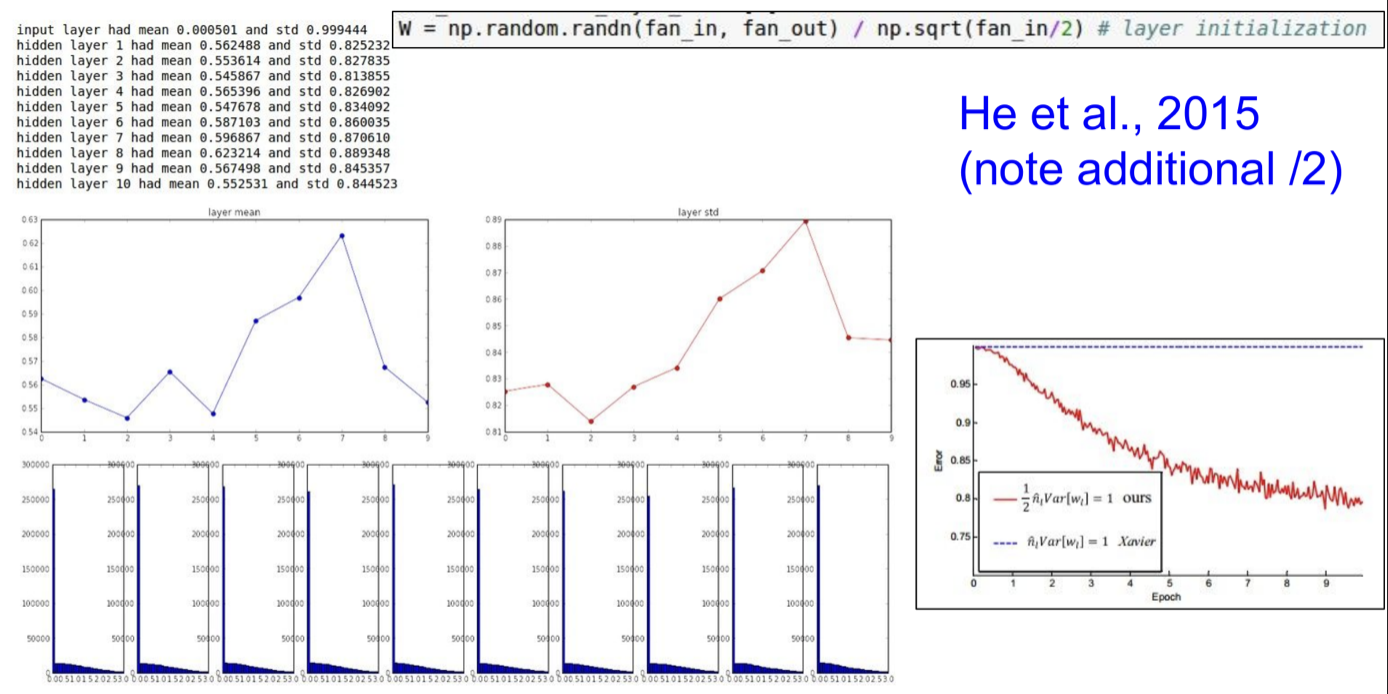
He Initialization은 Xavier에서 입력을 2로 나눈 초기화 방법이다.
-> Xavier를 사용하면 얻은 분산의 절반이 없어지므로, Xavier의 식에서 입력을 2로 나누게 되면 위와 같이 출력의 분포가 줄어들지 않게 된다.
Batch Normalization

Batch Normalization은 입력의 mini-batch별로 평균과 분산을 계산해서 normalize 하는 방법이다.
Layer를 통과한 후에도 분포가 gaussian이 되도록 하는 방법

주로 Fully connected layer나 Conv layer를 통과한 후에 데이터의 분포가 바뀌기 때문에, 이들을 통과한 후에 batch normalization을 수행하는 것이 일반적이다.
엄밀히 따지자면, Fully connected layer와 달리 Conv layer에서는 출력 Activation Map마다 평균과 분산을 가지고 정규화하게 된다.
그런데 문제는 gaussian 으로 바꾸는게 항상 옳지는 않다는 것이다.
(위 슬라이드에서와 같이 tanh를 사용한 경우) 약간의 saturation이 유용할 수도 있기 때문에 모두 gaussian이 되도록 하는 것이 좋지 않을 수도 있음)
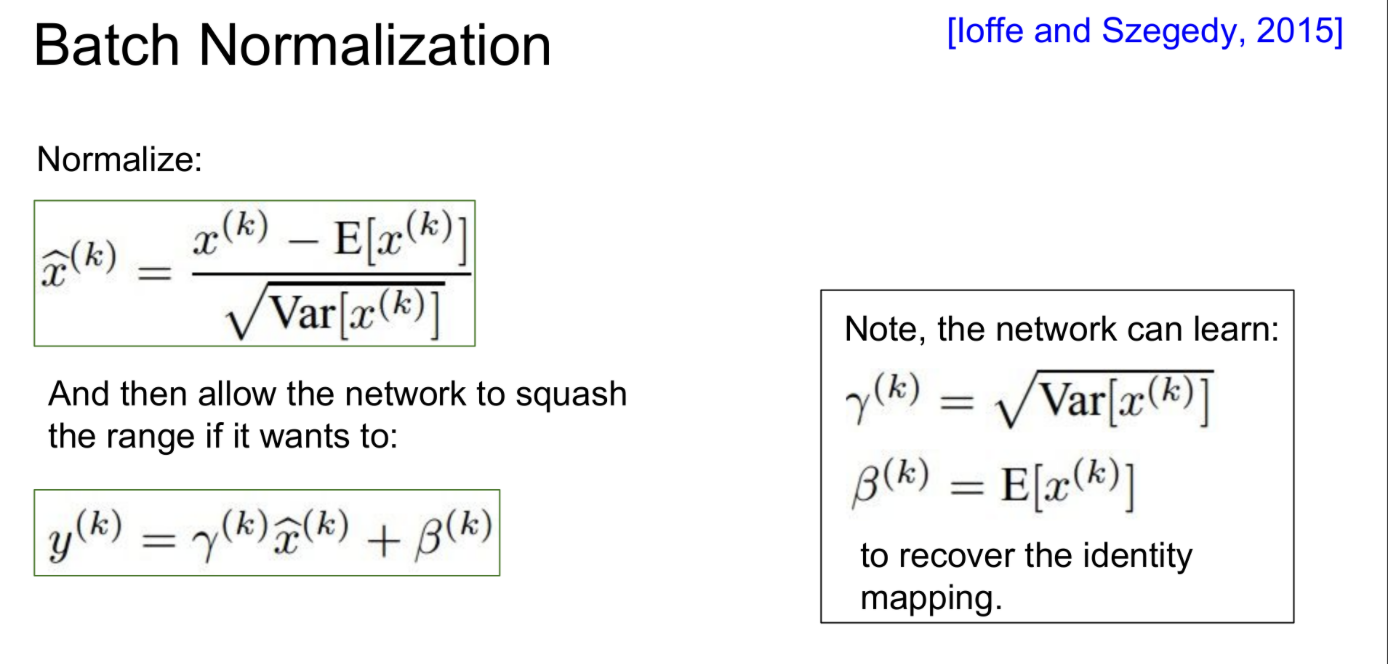
따라서, 추가로 scaling factor γ와 shifting factor β 를 두고 normalization의 정도가 유연하게 조절되도록 한다.
이 두 값은 backprop을 통해 학습되는 값이다.

Batch Normalization을 요약하면 다음과 같다.
-
입력이 주어지면 미니배치의 평균과 분산을 구하고 normalize한다.
이때, scaling factor γ와 shifting factor β로 normalization의 정도를 조절한다. -
Batch Normalization은 gradient flow를 향상시키고, 네트워크를 더 robust하게 해준다.
더 많은 learning rate와 다양한 initialization에서 동작하기 때문에 훈련하기 더 쉬워진다. -
Batch Normalization은 Regularization의 역할도 수행한다
각 layer의 입력(mini batch)은 표본이라고 볼 수 있으므로, 이들의 출력이 normalize되는 것은 각각 표본평균과 표본분산을 통해 normalize되는 것이라고 볼 수 있다. 이는 각 layer의 출력은 더이상 해당 mini batch에만 deterministic한 것이 아니라, 전체 데이터들에 영향을 받게 되는 것이라고 해석할 수 있다.
즉, X의 representation이 약간씩 jitter되면서 일종의 regularization 효과를 얻게 되는 것이다.
Test에서는 mean과 std를 계산하지 않고, training에서 구했던 값을 사용한다.
예를 들어, training에서의 moving average를 사용해서 값을 구하는 방법 등
Babysitting the Learning process
AI 학습의 전체 Flow를 다룬다.
Data preprocess
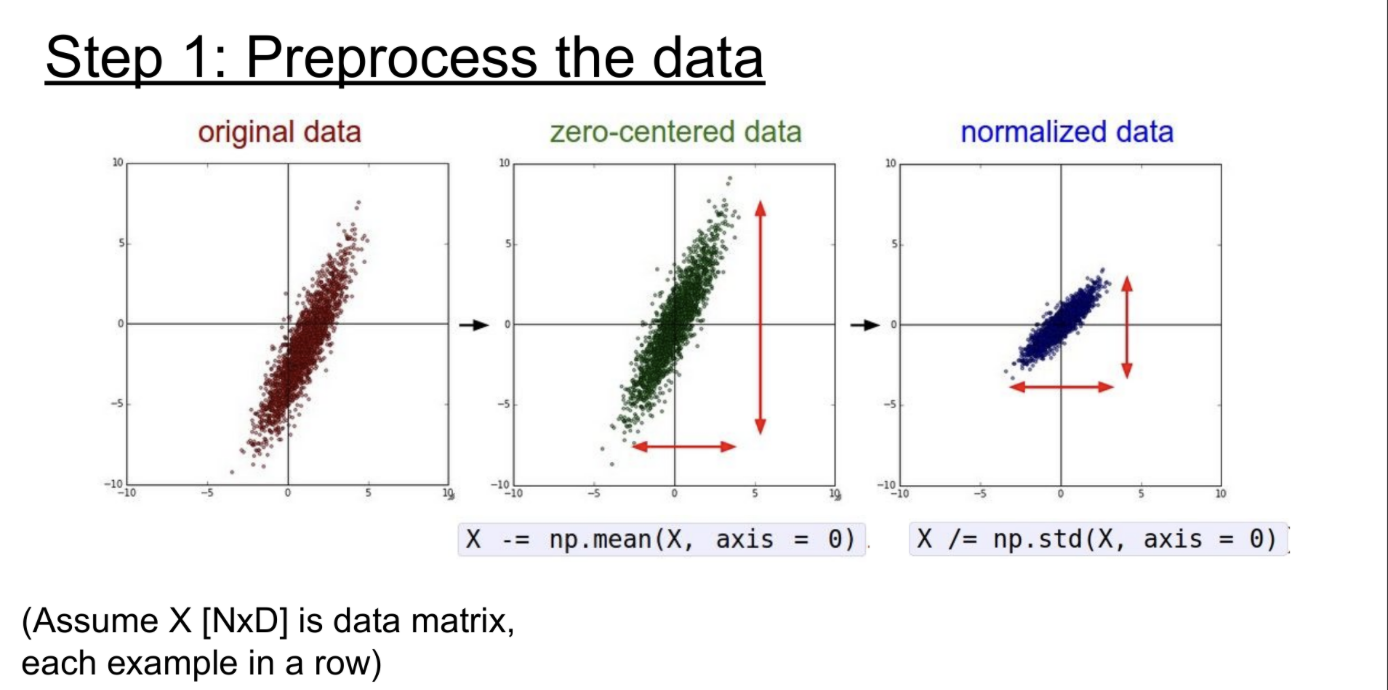
Choose the architecture(model)
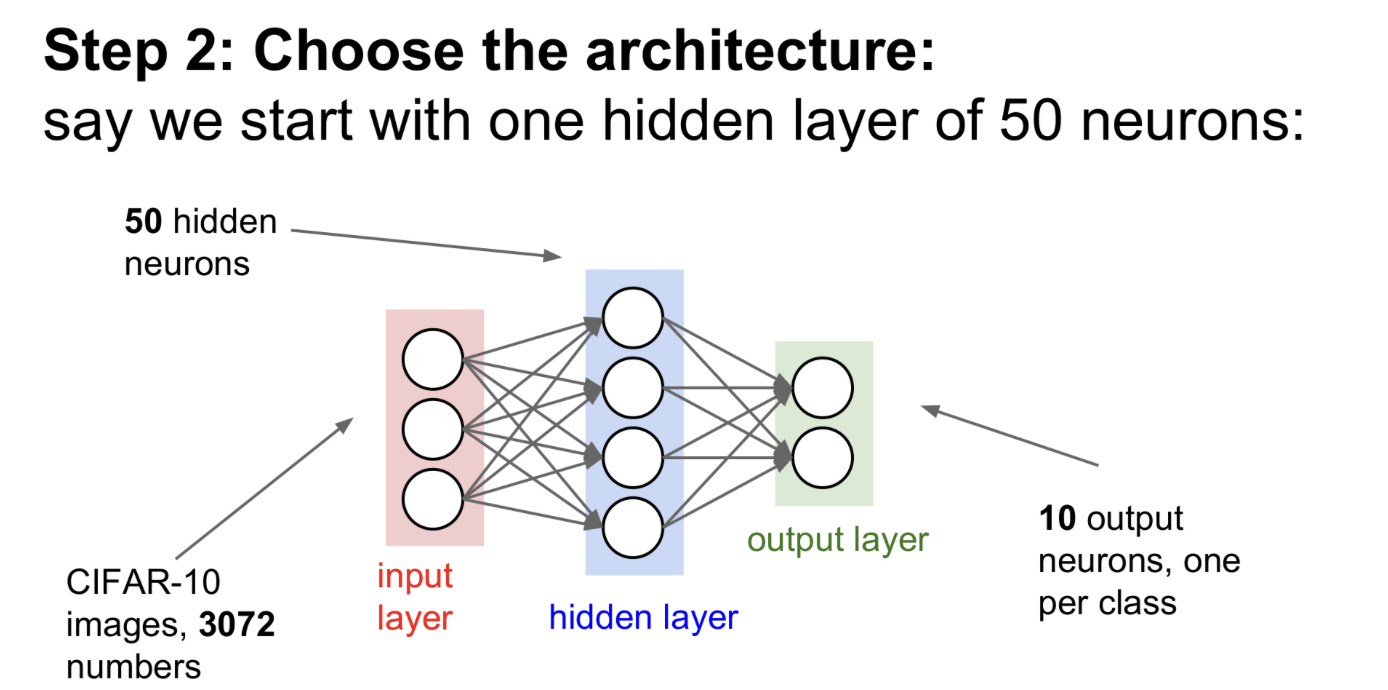
그리고, 모델의 구조를 선택한다
Ex) 50개의 뉴런을 가진 hidden layer로 설정
Loss function도 잘 동작하는지 검사
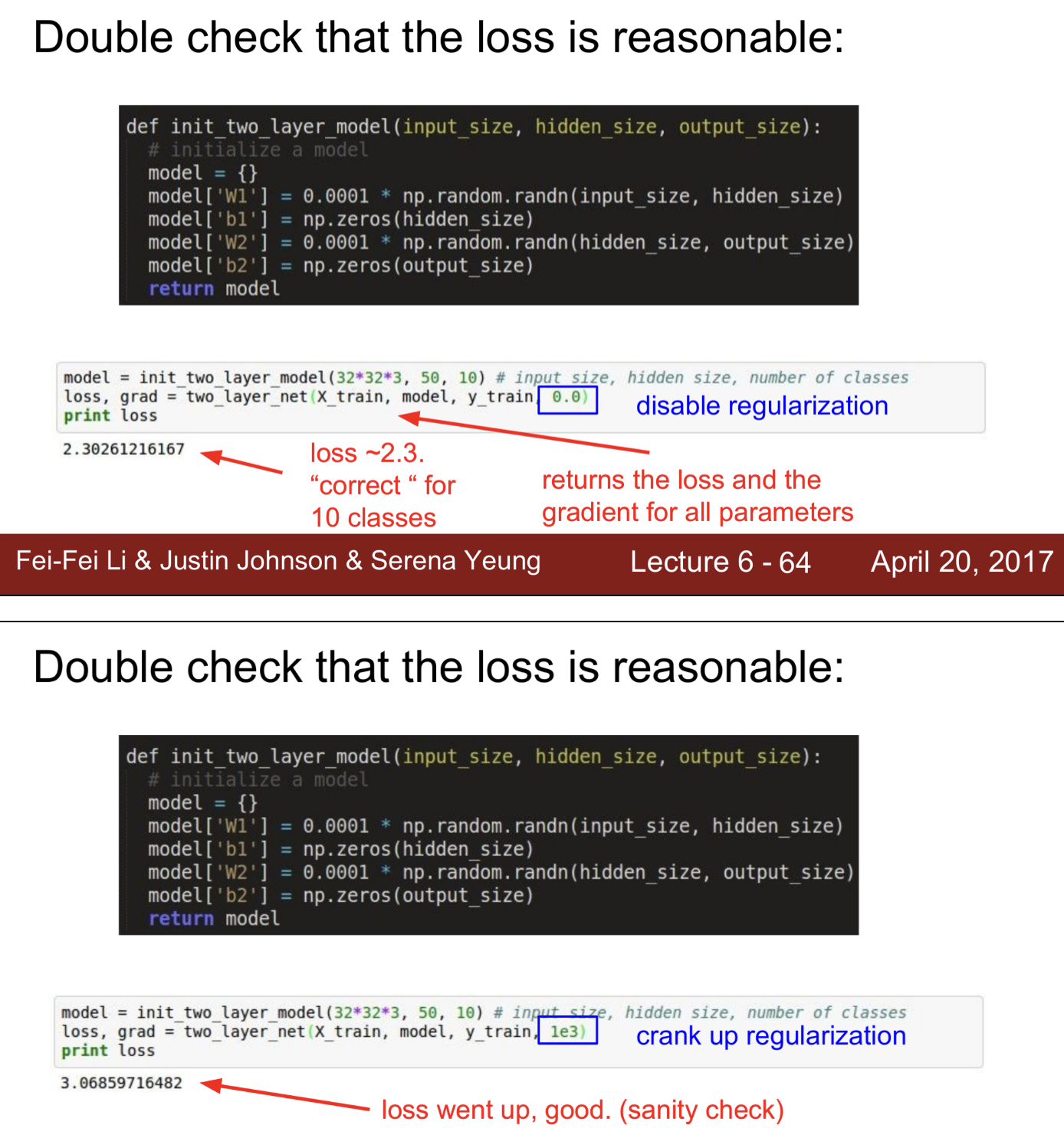
- Loss가 잘 계산되는지 검사 -> softmax를 사용하여 -log(1/class수)가 되어야 하기 때문에 -log(1/10) ~ 2.3이 나오는지 검사
- 약간의 Regularization을 주었을 때, Loss가 증가하는지 검사
start train
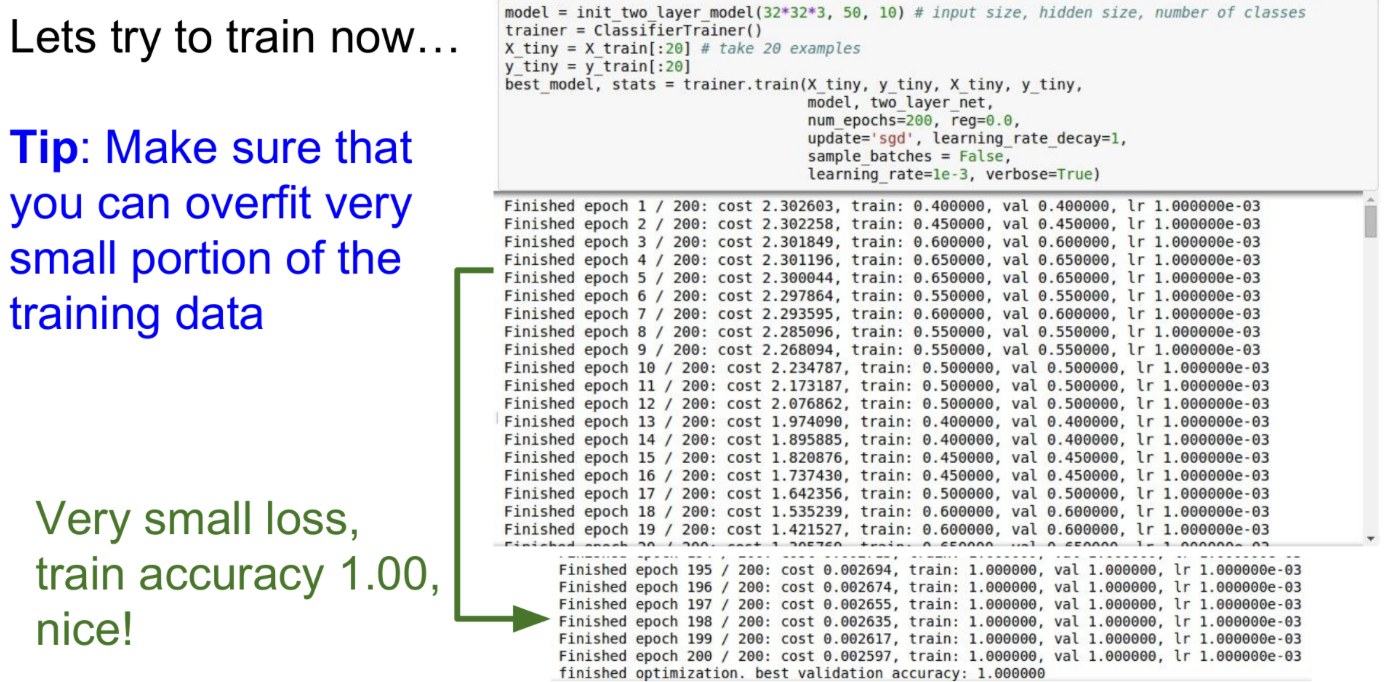
적은 데이터 안에서 overfit 할 수 있는지 먼저 확인

다음으로, 전체 데이터에서 학습한다.
약간의 regularization을 준 상태에서 최적의 learning rate을 찾는다.
이때, loss가 크게 변하지 않는다면, learning rate가 작은 경우이다.
위 슬라이드에서와 같이 loss는 큰 변화가 없지만 accuracy만 증가하게 되는 경우도 있다.(loss는 큰 변화 없지만, accuray는 20%까지 증가)
전체 확률은 널리 퍼져있고, softmax의 loss도 이와 매우 유사하다.
학습이 진행되면서 올바른 방향으로 전체 확률을 약간 이동시킨다면, loss는 여전히 분산되어 있지만 accuracy는 최대로 맞힌 횟수를 헤아리기 때문에 accuracy만 갑자기 증가할 수 있다.

learning rate를 크게하면(앞에서는 1-e6인데 여기서는 1e6), loss가 exploding하게 된다.

이러한 경우에는 다시 값을 줄여서 시도해보고, 그래도 크다면 조금 더 줄이고, 너무 작다면 다시 키우면서 최적의 learning rate를 찾아가면 된다.
Hyperparameter Optimization

overfitting을 방지하기 위해 Cross-validation strategy는 기본이다.
First stage
하이퍼파라미터 값을 넓은 범위에서 설정해보면서(coarse search), 잘 학습되는 적절한 하이퍼파라미터 범위를 찾는다.
몇번의 epoch동안만 돌려봐도 잘 동작하는지 알 수 있므로, 잘 동작하지 않는 경우 바로 학습을 중단하고 다시 잘 동작하는 범위를 찾는 과정을 반복한다.
Ex) 학습을 시작한 후, loss가 처음의 값보다 3배 이상으로 커진다면 아주 빠르게 증가한다는 의미이므로, 바로 중단하고 다른 값을 시도
Second stage
앞의 과정에서 찾은 적절한 범위에서 더 미세하게 찾는다. (fine search)
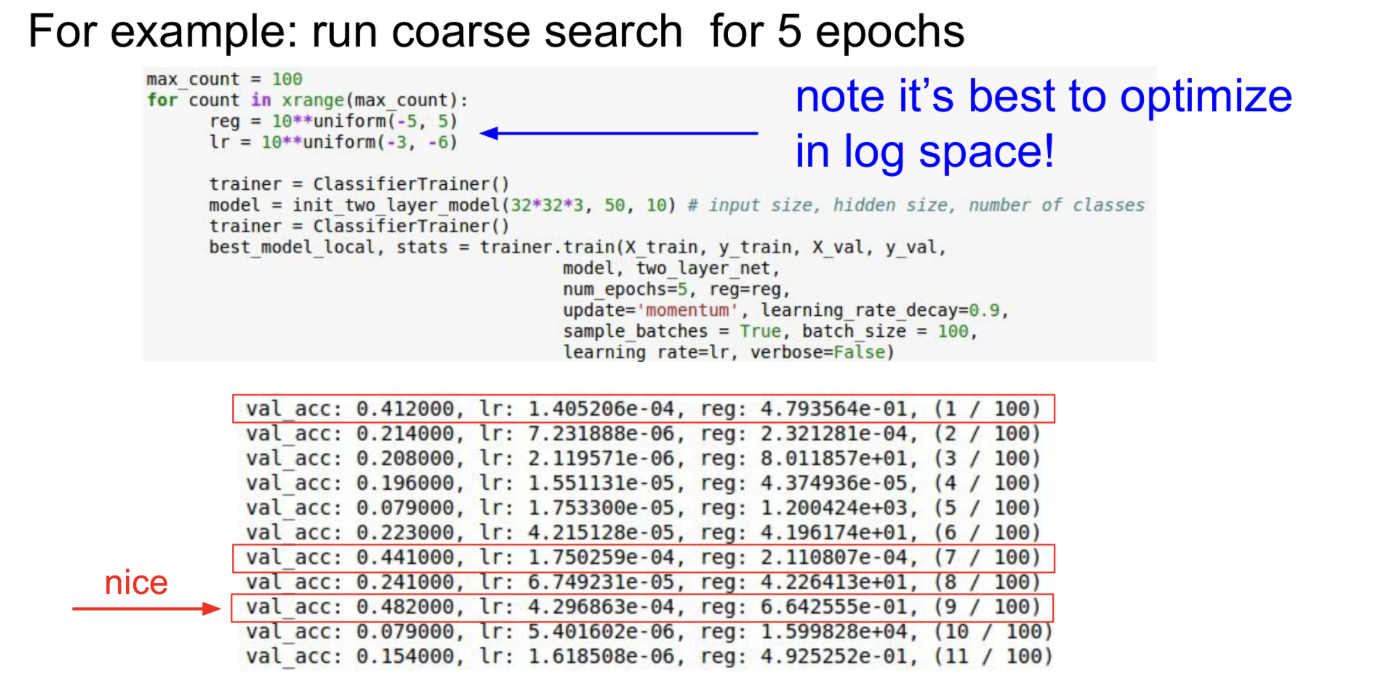
첫번째 단계인 넓은 범위에서 적절한 값의 범위를 찾는 과정 -> 빨간색 부분이 적절한 값의 범위이다.

앞에서 찾은 범위에서 다시 미세하게 찾아나간다.
위 슬라이드에서는 좋은 결과들을 빨간색 박스로 표시하였는데, 이들간의 learning rate에 큰 차이가 없는 범위내에서만 좋은 결과가 나오면 좋지 않다.(빨간글씨부분)
저 범위 외에 더 좋은 값이 있을 수도 있기 때문.
Random Search VS Grid Search
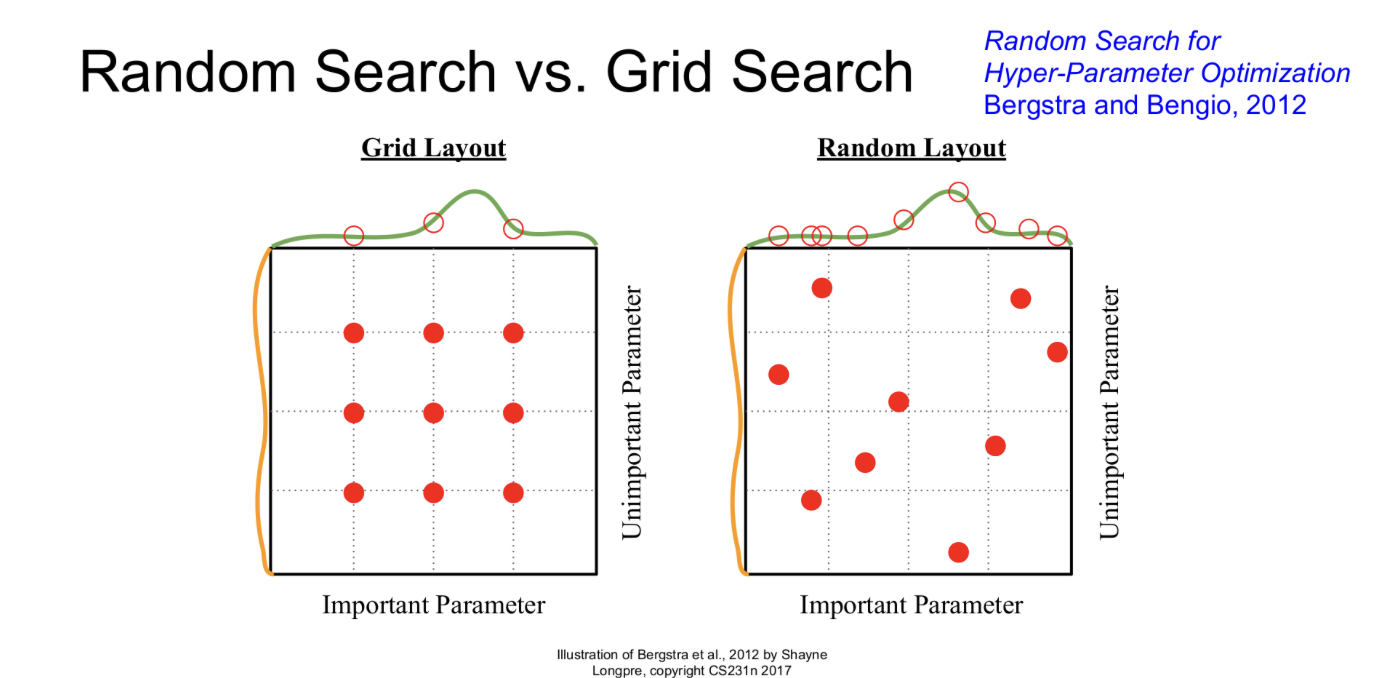
Hyperparameter를 탐색하는 방법은 위 슬라이드와 같이 2가지가 있는데, Grid Search에는 문제가 있다.
실제로는 오른쪽 그림에서와 같이 여러 parameter들이 다차원의 형태로 존재한다. 따라서, 왼쪽 그림과 같이 grid로 탐색하게되면 9번을 하더라도 다른 차원에서는 3번밖에 searching을 수행하지 않은 결과가 나타날 수 있다.
따라서, Random search로 탐색하면서 더 많은 범위를 볼 수 있는 방식을 사용하자

네트워크 구조, regularization 등의 모든 것들이 다 하이퍼파라미터이고, 이들도 모두 조정하면서 최적의 조합을 찾아야 한다.
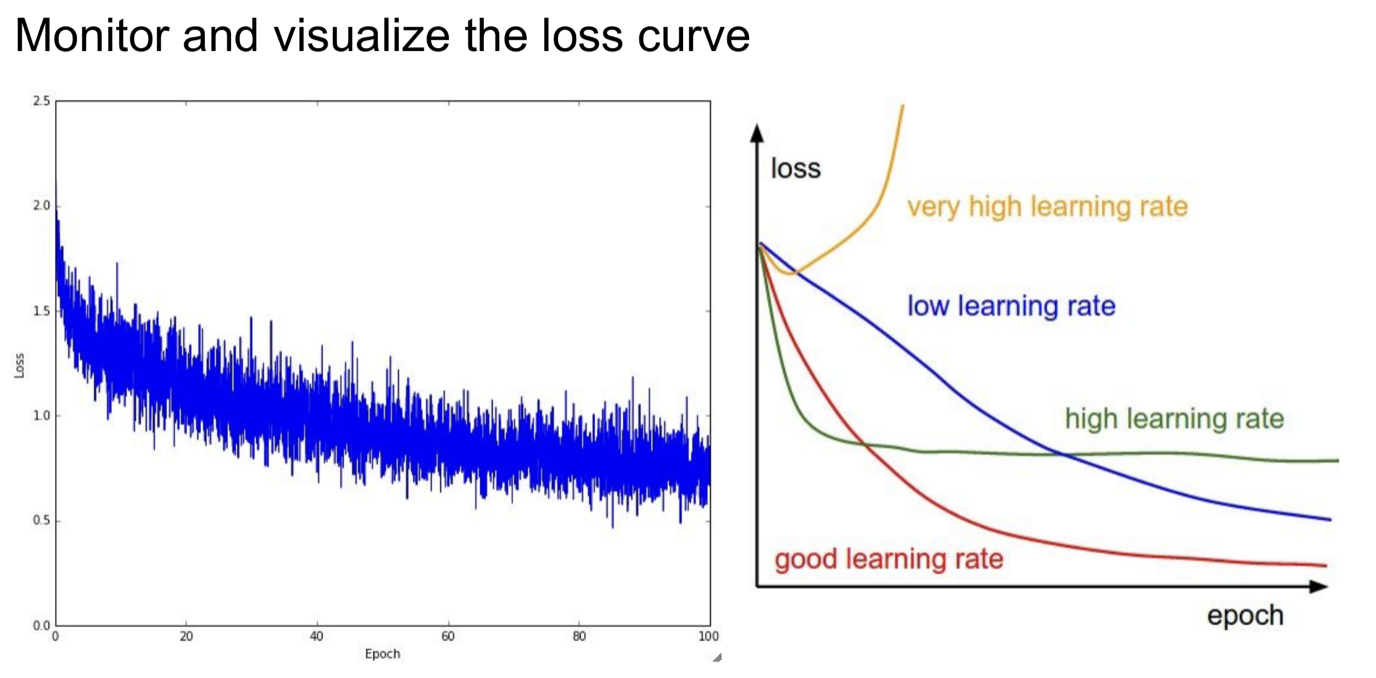
빨간색 곡선이 이상적인 형태의 loss curve이다.
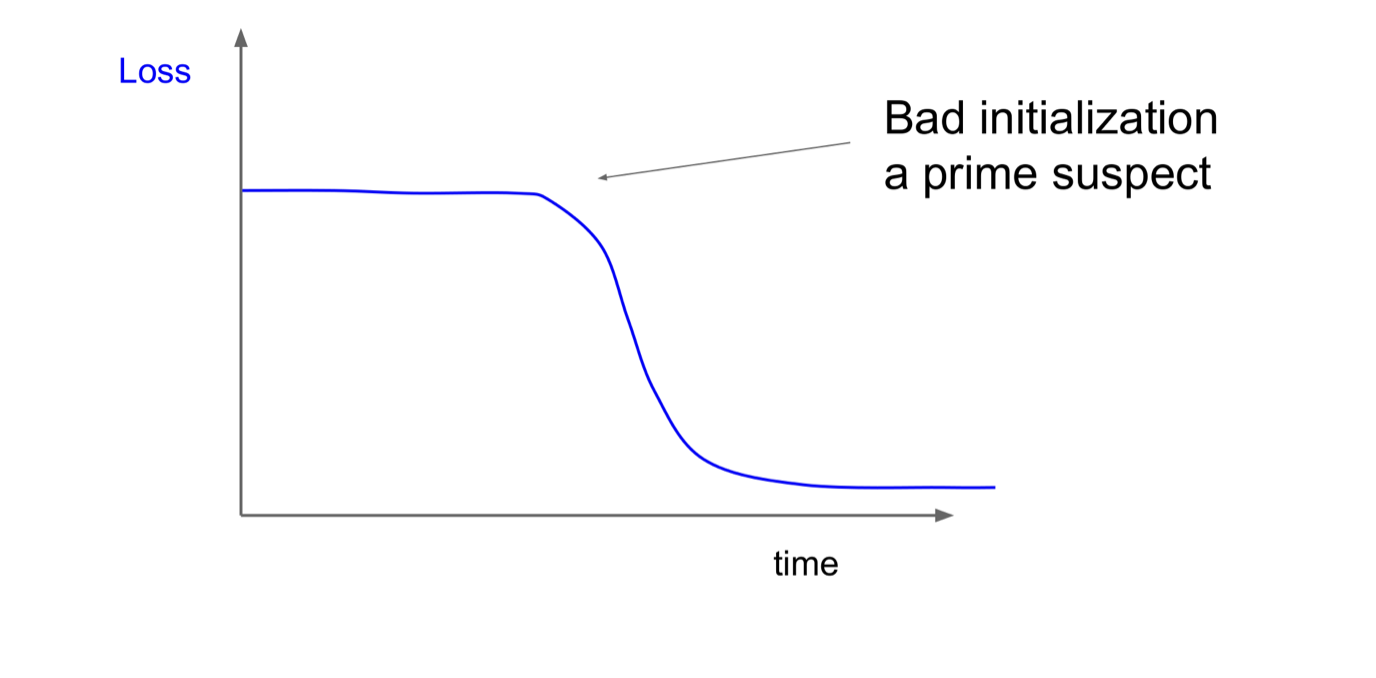
만약, 위와같은 그래프가 나타난다면, initialization이 제대로 수행되지 않았을 수 있다.
nitialization이 제대로 수행되지 않으면, 처음에 gradient가 제대로 흐르지 않아서 초기에 학습이 제대로 수행되지 않을 수 있음
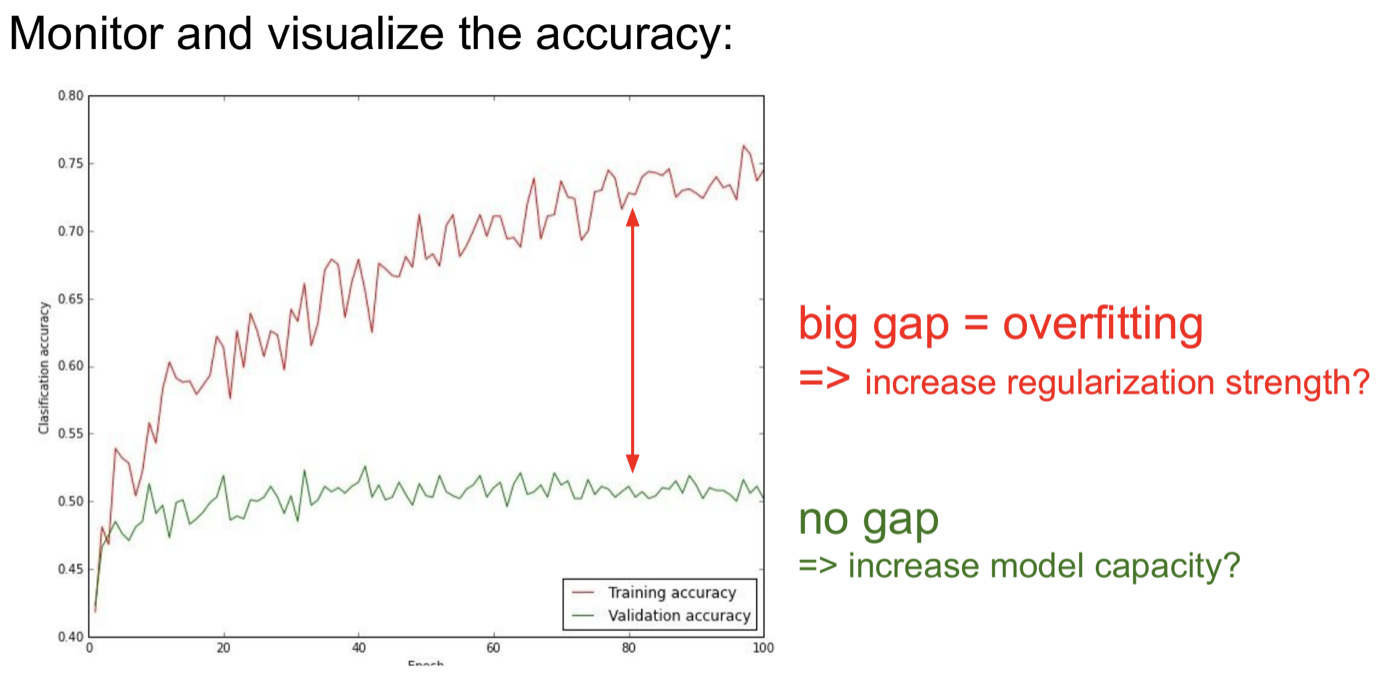
Train과 Validation의 Gap이다.
크다면 overfit이므로, regularization을 강도를 높여볼 수 있다.
작다면 underfit이므로, model의 크기를 더 키워볼 수 있다.
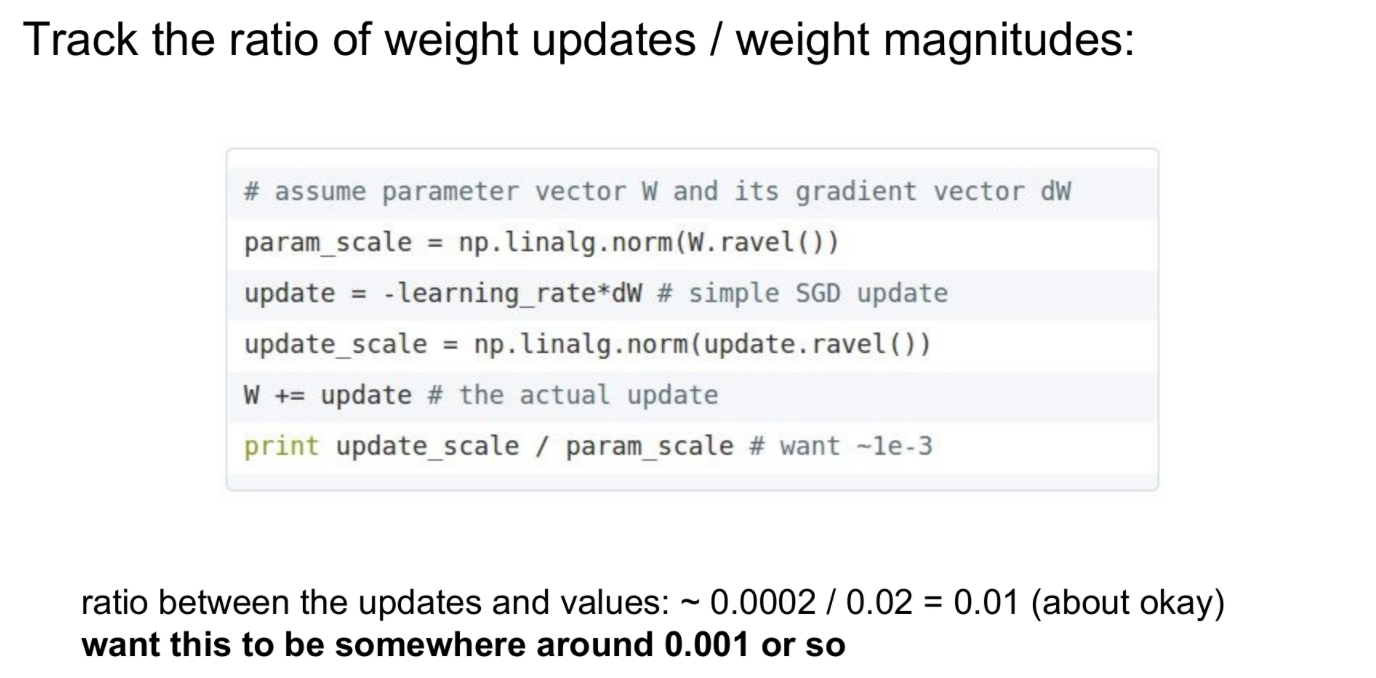
학습 중에 W의 파라미터 크기와 업데이트될 값의 크기를 각각 norm 연산을 통해 구한 후, 이들의 비율을 계산하면 업데이트가 잘 수행되는지 확인할 수 있다.
Ex) 업데이트가 파라미터에 비해 너무 많이 수행된다면 ratio가 매우 클 것이고, 너무 적게 수행된다면 ratio가 매우 작을 것이다.
이 방법은 학습에서 무엇이 문제가 되는지 확인하는 디버깅 용도로 사용 가능하다.

대강 어떻게 구성할지 정해준 점이 재밌다ㅎ 모델 구현을 더 경험해보며 실력을 쌓아야 겠다.

