Lecture 7은 성능을 올리기 위한 여러 방법들을 알려준다.
Optimizatation
SGD(Stochastic Gradient Descent)

가장 기본 Gradient Descent 이며 mini-batch 단위로 끊어서 loss를 계산하고 parameters를 업데이트 한다.
gradient 방향이 굉장히 크게 튀기 때문에 Zigzag path로 업데이트를 한다고 한다. 그래서 굉장히 느리고 비효율적이다.
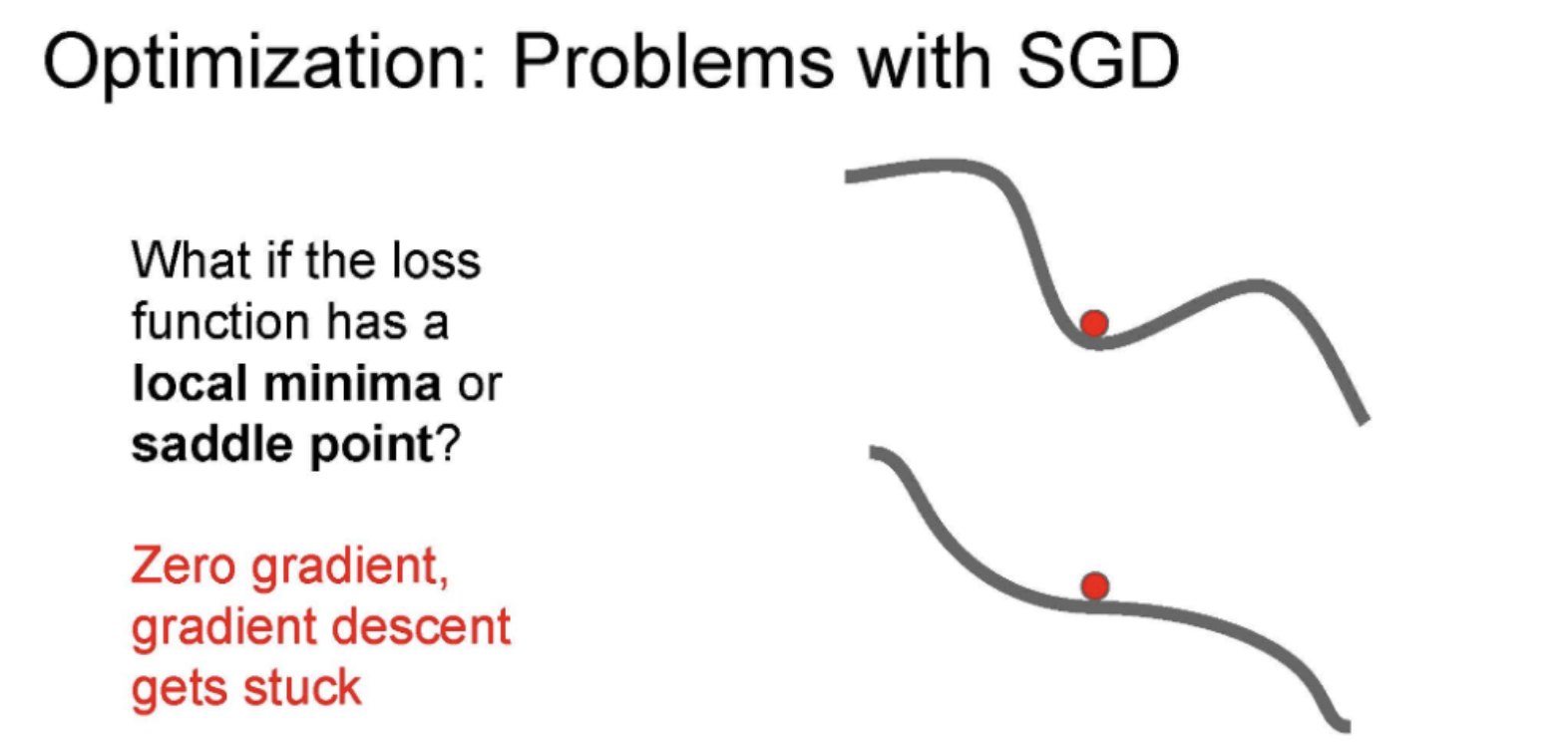
문제점으로 Local Minima/Saddle point가 소개되었는데 SGD같은 경우는 Local Minima나 Saddle point가 있는 부분에서 Zero gradient가 되어 더이상 업데이트를 안하고 멈춰버린다. Multi demension 상횡에서는 saddle point가 엄청 많이 존재한다고 한다. 이때 gradient는 너무 작아 굉장히 느리게 업데이트가 진행되는 큰 문제가 있다.
Momentum

Momentum에는 Velocity 라는 개념이 등장한다. Zero gradient 부분을 빠져나오기 위해 SGD 방식에 가속도를 추가한 방법이다.
vx가 속도를 나타내고, rho는 마찰계수다. (보통 0.9~0.99로 맞춤)
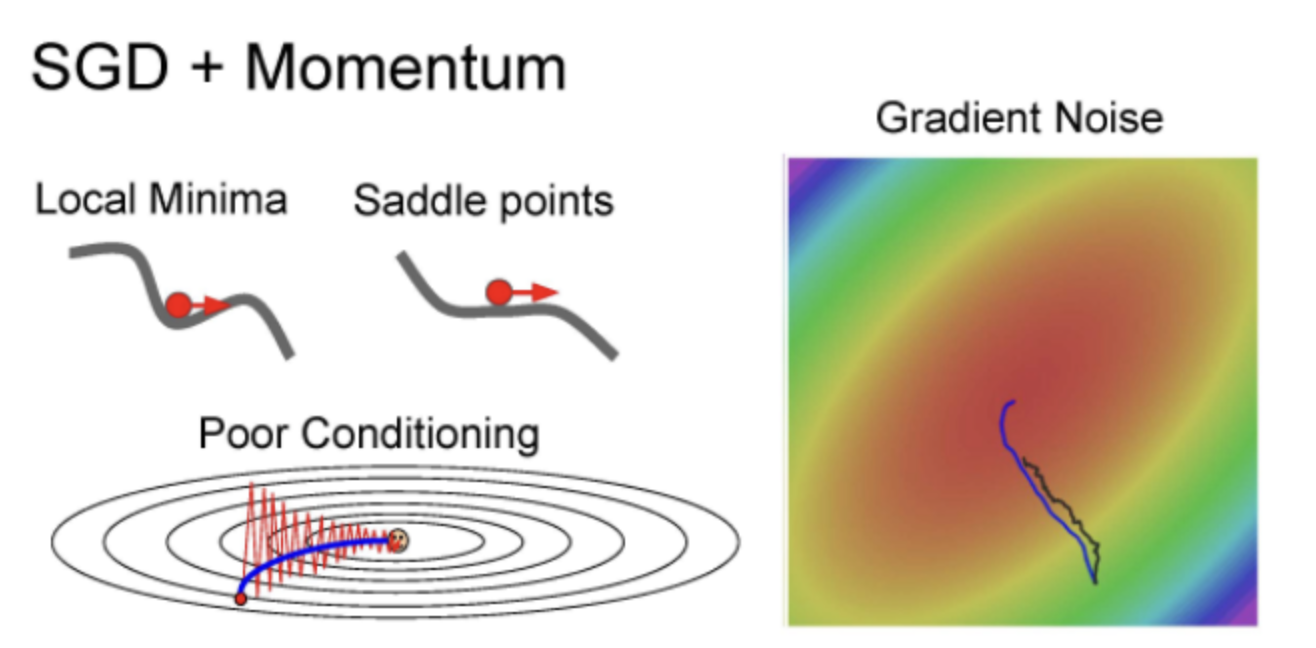
Momemtum은 loss에 덜 민감하여 수직 방향의 변동을 줄이고 수평 방향의 움직임을 점차 가속화하 노이즈를 줄여 SGD보다 local minima와 saddle points 에서도 더 안전한다.
비슷한 방식으로 Nesterov Momemtum을 소개해줬는데 기존 방법은 gradient를 계산하고 velocity와 합쳤지만, Nesterov는 velocity 방향으로 먼저 움직인 후 gradient를 계산한다.
Nesterov는 convex optimization에서 굉장히 뛰어난 성능을 나타내지만, 고차원에서의 deerp 러닝에서는 none-convex가 많아 뉴럴 네트워크(NN)에서 성능이 좋지 않다.
AdaGrad

AdaGrad는 Parameters를 갱신하는 알고리즘으로 training 중에 gradient를 활용하는 방법이다.
AdaGrad는 grad squared term을 이용한다. 학습 도중에 계산 되는 gradient를 제곱해서 더해주고, 업데이트 할 때 앞서 계산한 gradient 제곱근 항으로 나눠준다. 아래 그림을 보면 빨간색으로 밑줄 부분이 업데이트할때 제곱은 항으로 나눠주는 부분이다.

AdaGrad는 step을 진행할수록 값이 점점 작아지다보니 속도가 느려진다. AdaGrad도 convex 한 경우 minimum에 서서히 속도를 줄여서 수렴하여 좋지만, Non convex에서는 saddle point에 걸려 멈추는 문제가 생겨 업데이트가 되지 않는다. NN을 학습시킬 때 AdaGrad를 잘 사용하지 않는다.
RMSProb
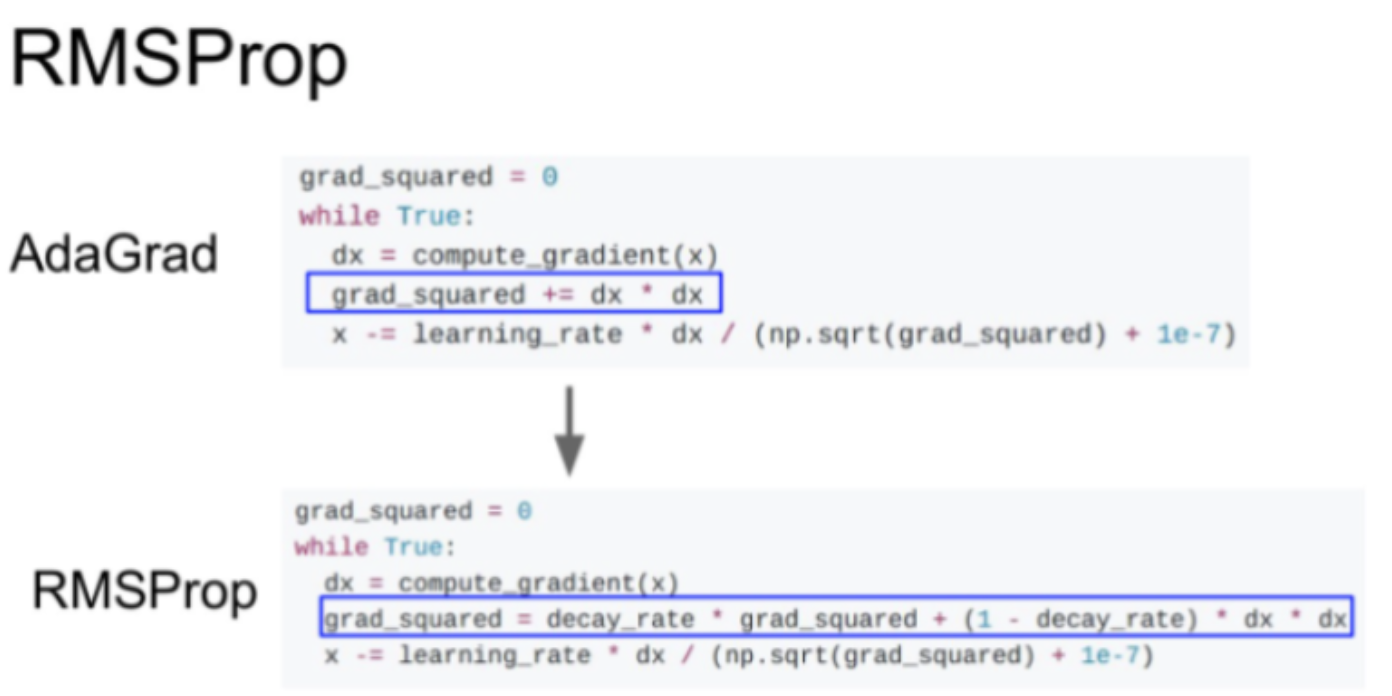
속도가 줄어드는 문제를 해결하기 위해 RMSProp라는 방법이 나온다. AdaGrad의 gradient 제곱항을 그대로 사용하지만, decay_rate(보통 0.9~0.99로 설정)를 곱해준다. 그리고 gradient 제곱은 (1-decay_rate)를 곱해주고 더해준다. 이렇게 하면 step의 속도를 효율적으로 가속/감속 시킬 수 있다고 한다.
Adam

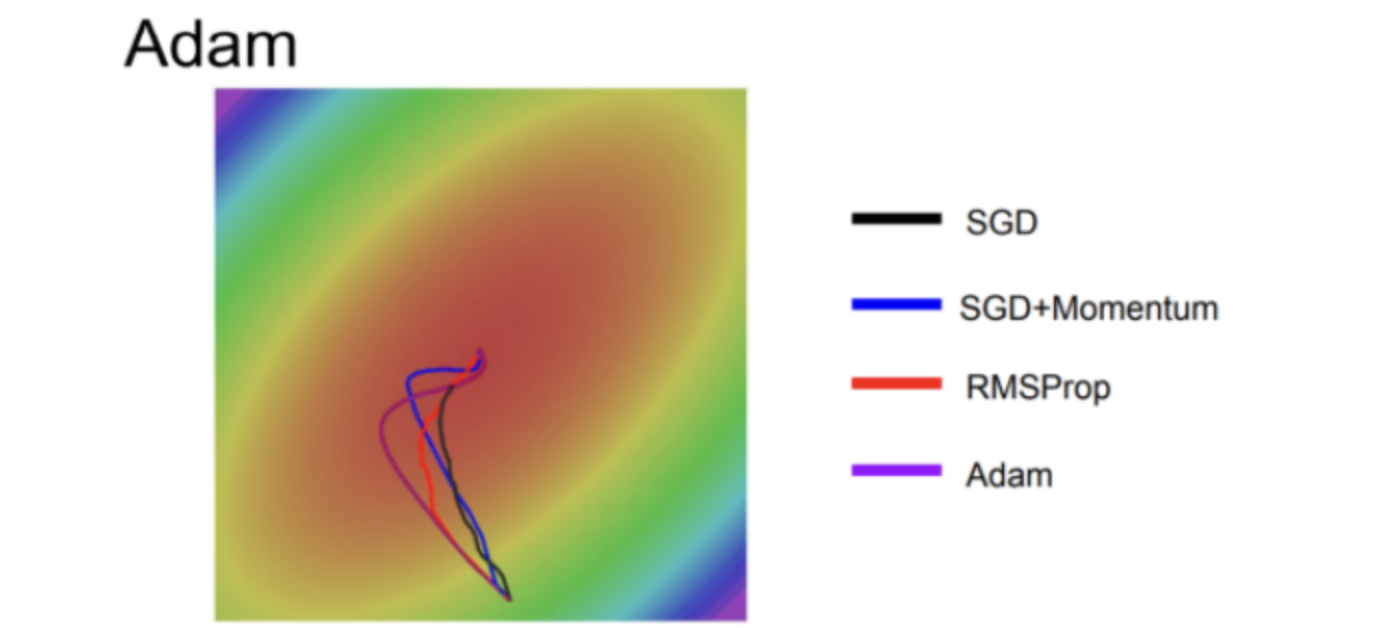
Momentum과 Ada를 합친 Adam은 더 최적화된 방법으로, 코드를 보면 First moment와 second moment를 이용해 이전 정보를 유지하고(Momentum 방법), AdaGrad나 RMSProp처럼 gradients의 제곱을 이용하는 방법이다.
이름만 그렇지 실제로는 Momentum과 RMSprop를 합친것과 유사하다.
그런데 초기 step에서 second_moment를 0으로 설정해 초기 step이 엄청 작아지는 문제가 발생될 수 있다. 그래서 Adam은 값이 튀지 않도록 보정항(bias)을 추가했다(1e-7는 나누는 값이 0이 되는 것을 방지한다).
First-Order Optimization
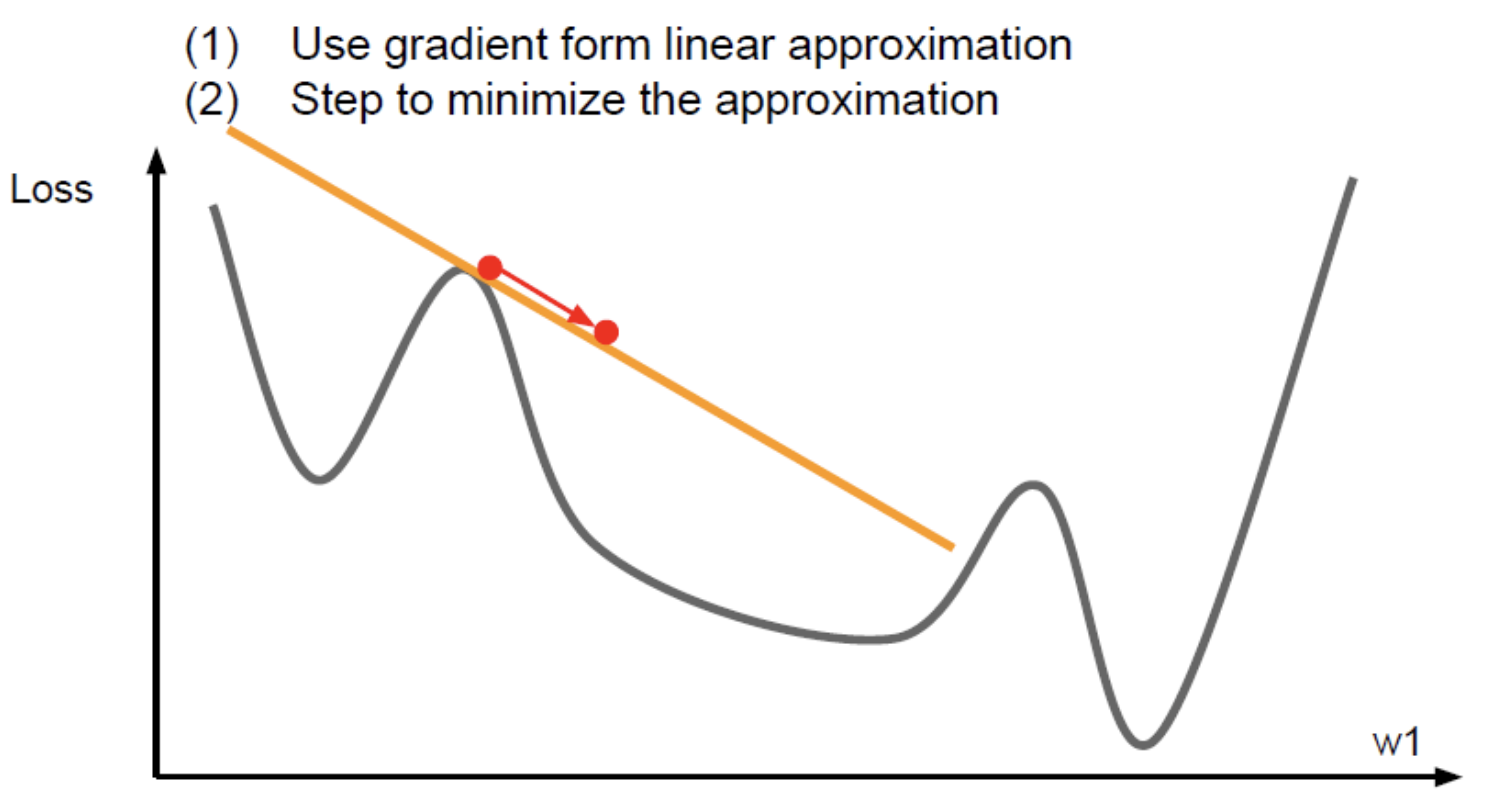
손실함수가 있다고 생각하면 현재 빨간점에 있고, 여기서 gradient 계산하는 것이다. 손실함수를 선형함수로 근사시키는 것을 1차 테일러 근사라고 한다. 이를 실제 손실함수라 생각하고 step을 계속해서 내려간다. 실제로 멀리갈 순 없다. 1차 미분값이기 때문에.
Second-Order Optimizaion
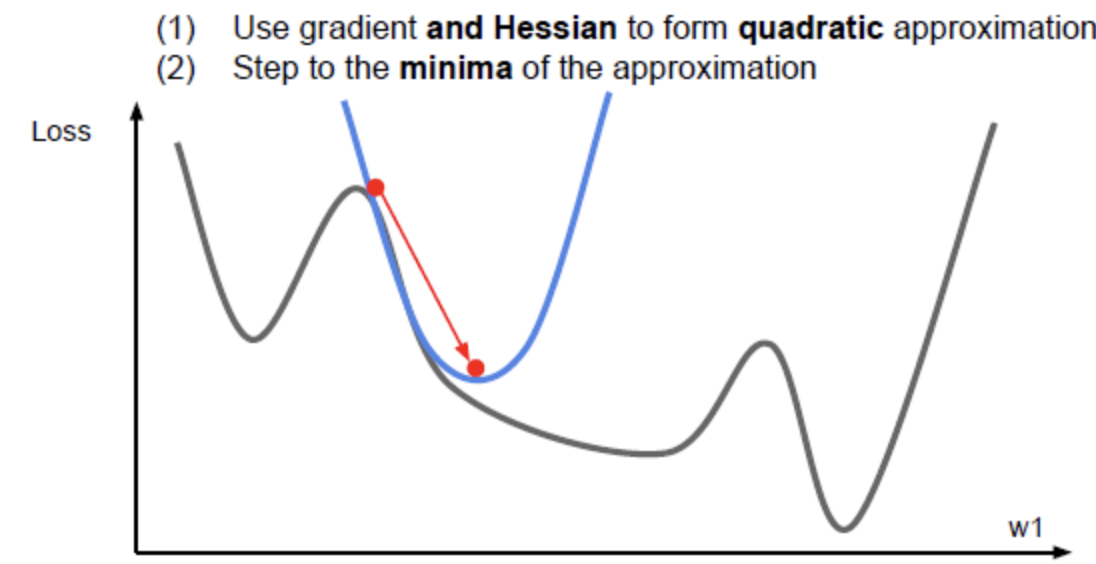
2차 근사를 이용하면 minima에 더 잘 접근할 수 있다. 2차 근사 함수의 minima로 이동. learning rate가 불필요. 매 step마다 minima의 방향으로 이동하기 때문에 learning rate가 없다. Optimization 알고리즘들은 training error를 줄이고 손실함수를 최소화 시키기 위한 역할을 수행한다. Training error 보다 Train/Test error 격차를 줄이는게 더 중요하고, 가장 중요한 것은 validation set의 성능을 최대화 시키는 것이다.
Ensemble
다수개의 모델을 만들어 훈련시키고 다수의 모델 결과의 평균을 이용하는 방법이다.
여기서는 3가지의 대표 Ensemble 기법중 Voting을 소개하는 것 같다.
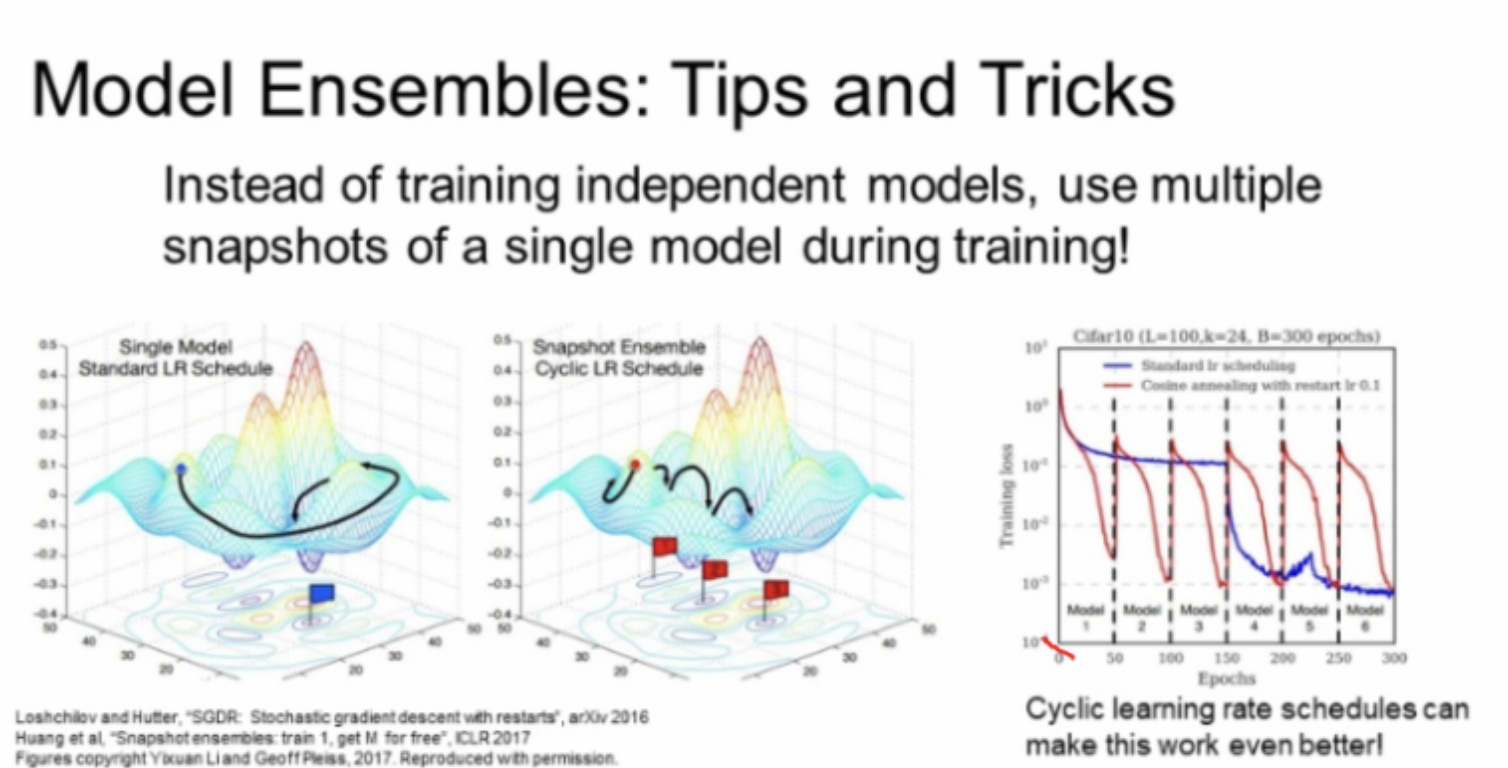
다른 방법으로, 모델을 독립적으로 학습시키지 않고, 학습 도중 모델을 snapshot하고 Ensemble을 사용할 수 있다.그리고 test에서 여러 snashot에 나온 예측값을 평균을 내어 사용한다.
즉 앙상블을 사용하면 다수의 모델을 만들어 내는데 시간이 걸려, 한 모델안에서 10개의 구간을 두고 앙상블처럼 사용하는 방법이다. 위 그림을 보면 train loss가 반복적으로 증감하는데, 이는 learning rate를 반복적으로 조절해 손실함수에 다양한 지역에서 수렴하도록 위해서다.
Regularlization

앞에서 배운 Overfitting을 방지하기 위한 L1과 L2 Regularliztion이다.
NN에서는 잘 사용되지 않는다고 한다.
Dropout
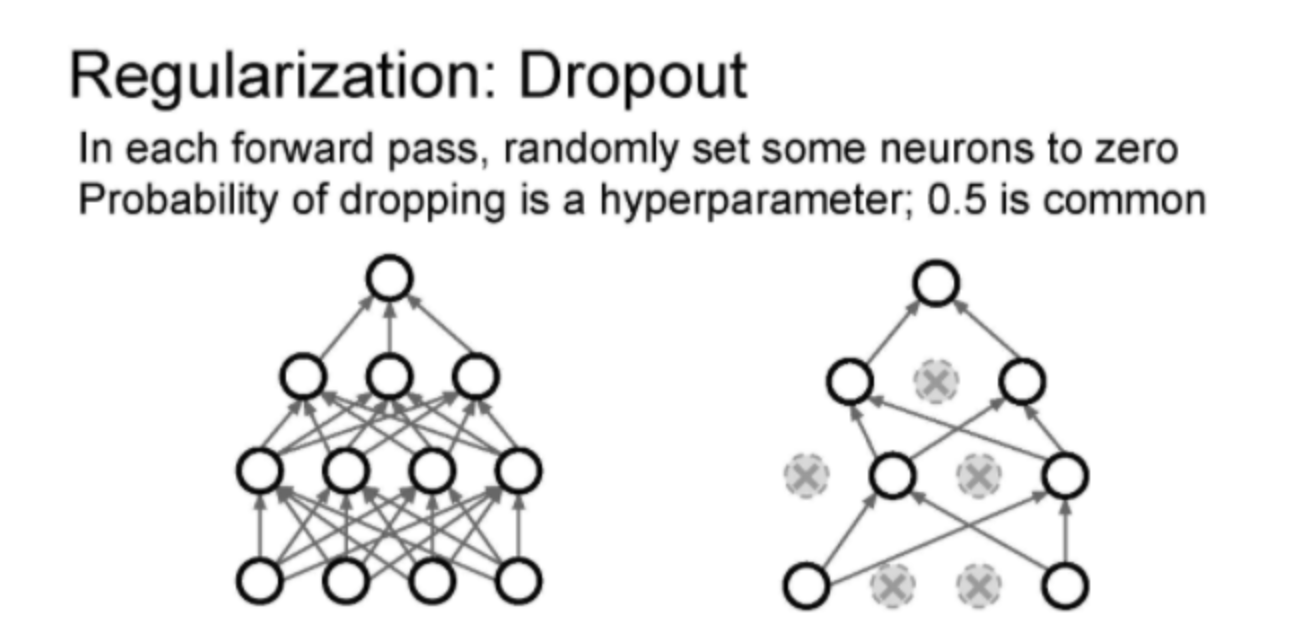
forward pass 과정에서 일부 Neuron을 0으로 만드는 방이다.
forward pass iteration 마다 모양이 바뀌는데, 현재의 activatons의 일부를 0으로 만들어 다음 레이어의 일부가 0과 곱해지게 하는 것이다. Dropout의 특징은 상호작용을 방지하는 것이다.
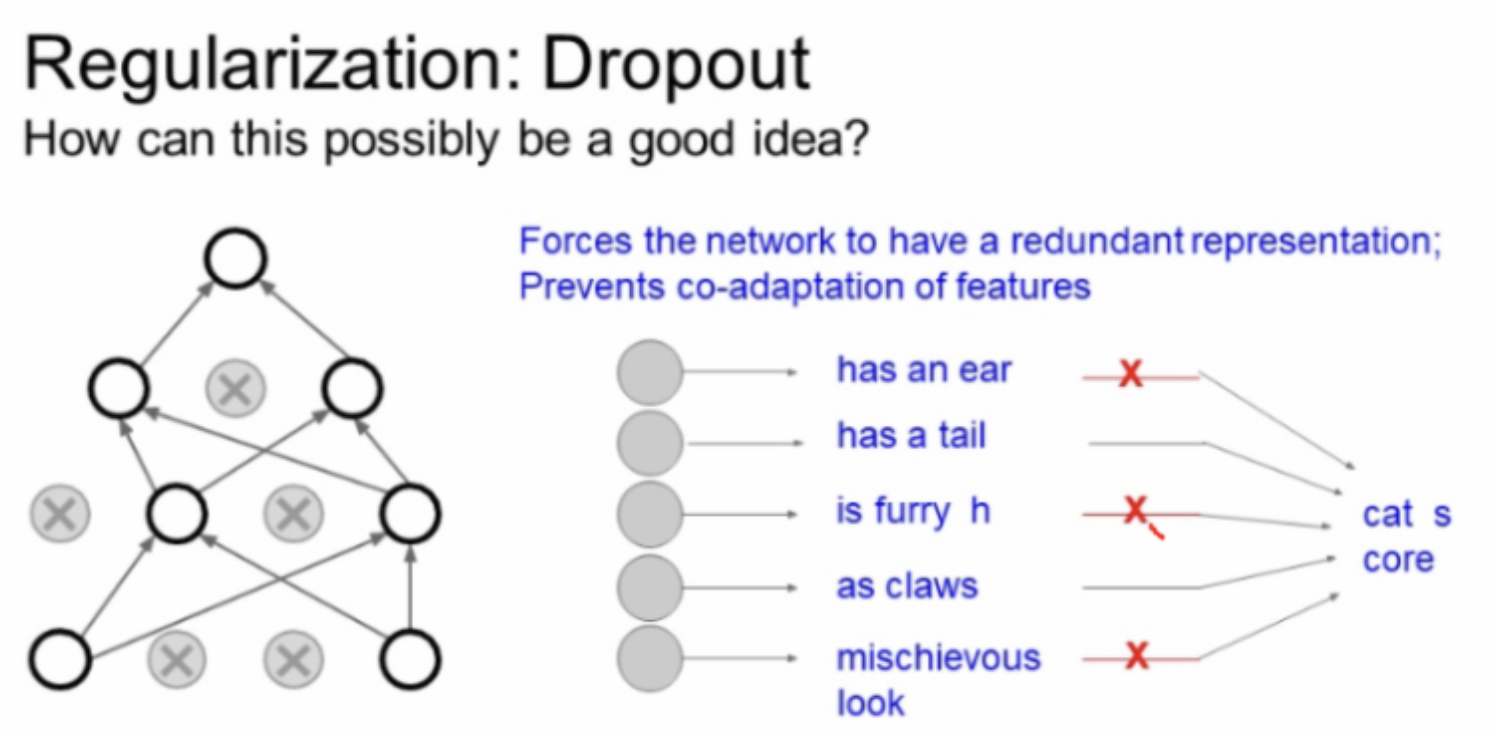
다양한 Features 사용을 막아 Overfitting을 방지한다. 모든 정보가 Classification task 수행에 필요하지 않다는 컨셉이다.
학생들의 질문이다.
무엇을 0으로 두는지? activation을 0으로 놓는다.
각 레이어에서 next activ= prev activ * weight 으로 계산하고, 현재 activations의 일부를 0으로 만들면 다음 레이어의 일부는 0과 곱해질 것.
어떤 layer에서 사용하는지?
fc layer에서 주로 사용하지만 conv layers에서도 종종 볼 수 있다. conv layers는 channels이 있기 때문에 일부 channel 자체를 dropout 시킬 수 있다
Dropout은 특징들 간의 상호작용(co-adaptation)을 방지한다고 볼 수 있다. 이는 overfiting을 막아주는 것과 관련이 있다. 그래서 Dropout은 단일 모델로 앙상블 효과를 가질 수 있다.

z가 임의적으로 0이 되면 f(x)의 값이 0이 되기 때문이다. 네트워크가 이미 학습된 네트워크의 test time에는 이러한 임의성(stochasticity)가 적절하지 않다. 대신 임의성을 average out 시켜 버린다. Dropout을 사용하게 되면 전체 학습시간이 늘어난다. 각 스텝마다 업데이드되는 파라미터의 수가 줄어들기 때문이다. 다시 말해 Dropout을 사용하게 되면 전체 학습시간은 늘어나지만 모델이 수렴한 후에는 더 좋은 일반화 능력을 얻을 수 있다.
Batch Normalization
Batch normalization 또한 이와 비슷한 동작을 할 수 있다. Train time의 BN를 상기해보면 mini batch로 하나의 데이터가 샘플링 될 때 매번 서로 다른 데이터들과 만나게 된다.
Train time에서는 각 데이터에 대해서 이 데이터를 얼마나 어떻게 정규화시킬 것인지에 대한 stochasticity이 존재했다. 하지만 test time에서는 정규화를 mini batch 단위가 아닌 global 단위로 수행함으로써 stochasticity를 평균화 시킨다. 이런 특성 때문에 BN 은 Dropout과 유사한 Regularization 효과를 얻을 수 있었다.
Train time에는 stochasticity(noise)가 추가되지만 Test time에서는 전부 평균화 되기 때문이다. 실제로 BN을 사용할 때는 Dropout을 사용하지 않는다.
BN에도 충분히 regularization 효과가 있기 때문이다. 하지만 여전히 Dropout은 쓸모 있다. 우리가 자유롭게 조절할 수 있는 파라미터 p가 있기 때문이다. BN에는 하이퍼 파라미터가 없다.
Data Augmentation
이러한 Regularization 패러다임에 부합하는 또 한가지 전략이 바로 data augmentation 이다. 기본 버전의 학습과정에서는 데이터가 있고 레이블이 있고 이를 통해 매 스텝 CNN을 업데이트했다. 하지만 그 대신 train time에 이미지를 무작위로 변환시켜 볼 수 있다. 레블은 그대로 놔둔 채로 가능하다.

-Flib-

-Crob-
일반적으로 data augmentation는 어떤 문제에도 적용해 볼 수 있는 아주 "일반적인 방법" 이라고 할 수 있다. 어떤 문제를 풀려고 할 때, 이미지의 label을 바꾸지 않으면서 이미지를 변환시킬 수 있는 많은 방법들을 생각해 볼 수 있다. Train time에 입력 데이터에 임의의 변환을 시켜주게 되면
일종의 regularization 효과를 얻을 수 있다. 그 이유를 다시 정리해보면 train time에는 stochasticity가 추가되고 test time에는 marginalize out 되기 때문이다.
DropConnect
DropConnect은 activation이 아닌 weight matrix를 임의적으로 0으로 만들어주는 방법이다. Dropout과 동작이 아주 비슷하다.
Fractional Max Pooling
fractional max pooling에서는 pooling연산을 수행 할 지역이 임의로 선정된다.
test time에 stochasticity를 average out 시키려면 pooling regions를 고정시켜 버리거나 혹은 여러개의 pooling regions을 만들고 averaging over 시킨다.
많이 사용하는 방법은 아니지만 참 좋은 아이디어라고 설명한다.
Transfer learning
Transfer learning은 "CNN 학습에는 엄청많은 데이터가 필요함"
이라는 미신을 무너뜨려버린다. 이때까지 overfitting의 원인을 소규모 데이터라 많이 꼬집었는데, 여기서는 소규모 데이터를 학습하면서 과적합에 대해 Regularization 대신 해결할 수 있는 방법 중 또 하나인 Transfer learning을 소개해준다.

이 CNN을 가지고 우선은 ImageNet과 같은 아주 큰
데이터셋으로 학습을 한번 시킨다. 이정도 데이터셋이면 전체 네트워크를 학습시키기에 충분한 양이다. 여기서 할 일은 Imagenet에서 학습된 features를 우리가 가진 작은 데이터셋에 적용하는 것이다.
그런데 이제는 1000개의 ImageNet 카테고리를 분류하는 것이 아니라 10종의 강아지를 분류하는 문제를 풀 수 있다. 데이터는 엄청 적고 Class는 겨우 10개 뿐이다.
일반적으로 떠올릴 수 ㅇ있는 방법은 우선 가장 마지막의 FC Layer는 최종 feature와 class scores간의 연결인데 이를 초기화시킨다.
기존에 ImageNet을 학습시킬 때는 4,096 x 1,000 차원의 행렬이었다. 그리고 방금 정의한 가중치 행렬은 초기화시킨다. 그다음 나머지 이전의 모든 레이어들의 가중치는 freeze시켜버리는 것이다. 그렇게 되면 linear classifier를 학습시키는 것과 같다. 오로지 마지막 레이어만 가지고 데이터를 학습시키는 것이다. 이 방법은 사용하면 아주 작은 데이터셋일지라도 아주 작 동작하는 모델을 만들 수 있다. 만일 데이터가 조금 더 있다면 전체 네트워크를 fine-tuning 할 수 있다.
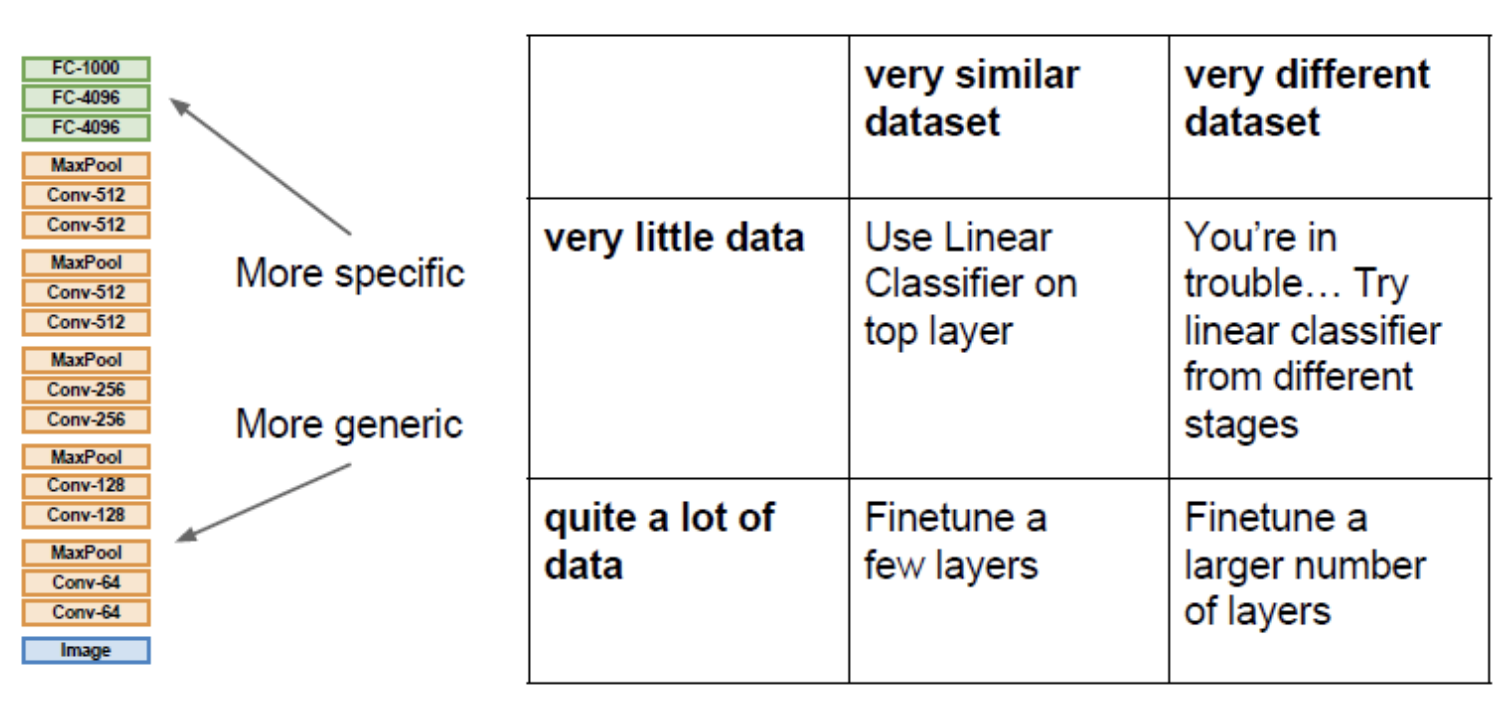
Transfer learning with CNNs


