본 글은 칸아카데미의 미적분 - 미분법에 대해서 공부하고 정리한 글입니다.
1. 지수 함수 / 로그 함수의 미분
자연상수 e에 대한 지수 함수(ex)와 로그 함수(ln=loge)에 대한 도함수를 알아보자.
1.1. 지수 함수
자연 상수에 대한 지수 함수의 도함수는 본래의 함수와 동일하다.
이를 다르게 표현하면 ex=a일 때, 이에 대한 기울기도 a이다.
f(x)=ex,f(x)′=ex
지수 함수 증명
위에 대한 내용은 아래와 같이 증명할 수 있다.
1️⃣ 먼저 자연 상수 e는 아래와 같이 정의할 수 있다.
e=limn→∞(1+n1)n=limn→0(1+n)n1
2️⃣ 도함수의 정의를 이용하여 다음과 같이 수식을 전개할 수 있다.
∂x∂[ex]=Δx→0limΔxex+Δx−ex=Δx→0limΔxex⋅eΔx−ex=exΔx→0limΔxeΔx−1
3️⃣ Δx 를 임의의 n에 관한 수식으로 바꿔준다.
n1+nln(1+n)=eΔx−1=eΔx=Δx⋯(1)⋯(2)⋯(3)
위의 수식에 따라서 Δx→0 인 경우, (1) 수식에 대입하면 알 수 있듯이 n→0 이다.
4️⃣ 3번 식에 따라 2번 식의 Δx를 n 에 관한 식으로 바꿔준다.
∂x∂[ex]=exn→0limln(1+n)n⋅n1n1=exn→0limn1ln(1+n)1=exn→0limln((1+n)n1)1=exln(limn→0(1+n)n1)1=exln(e)1=ex⋅11=ex※aln(b)=ln(ba)※e=n→0lim(1+n)n1
그럼 위의 전개를 통해서 ∂x∂[ex]=ex 임을 알 수 있다.
1.2. 로그 함수
자연 상수에 대한 로그 함수의 도함수는 아래와 같다.
이를 다르게 표현하면 lnx=a일 때, 이에 대한 기울기는 a1이다.
f(x)=lnx,f(x)′=x1
로그 함수 증명
위에 대한 내용은 아래와 같이 증명할 수 있다.
1️⃣ 도함수의 정의를 이용하여 다음과 같이 수식을 전개할 수 있다.
∂x∂[lnx]=Δx→0limΔxln(x+Δx)−ln(x)=Δx→0limΔxln(xx+Δx)=Δx→0limΔx1⋅ln(1+xΔx)=Δx→0limln((1+xΔx)Δx1)※lna−lnb=lnba※aln(b)=ln(ba)
2️⃣ Δx 를 임의의 n에 관한 수식으로 바꿔준다.
nnxn1⋅x1=nx1=xΔx=Δx=Δx1⋯(1)⋯(2)⋯(3)
위의 수식에 따라서 Δx→0 인 경우, (1) 수식에 대입하면 알 수 있듯이 n→0 이다.
3️⃣ 2번 식에 따라 1번 식의 Δx를 n 에 관한 식으로 바꿔준다.
∂x∂[lnx]=n→0limln((1+n)n1⋅x1)=x1n→0limln((1+n)n1)=x1ln(n→0lim(1+n)n1)=x1ln(e)=x1※e=n→0lim(1+n)n1
지수 함수의 증명과 마찬가지로 위의 전개를 통해서 ∂x∂[lnx]=x1 임을 알 수 있다.
2. 삼각 함수의 미분
2.1. 삼각 함수의 덧셈 정리
기본적인 삼각함수의 덧셈 공식에 대해서 짚고 넘어가보자.
sin(−a)cos(−a)sin(a+b)sin(a−b)cos(a+b)cos(a−b)=−sin(a)=cos(a)=sin(a)⋅cos(b)+sin(b)⋅cos(a)=sin(a)⋅cos(b)−sin(b)⋅cos(a)=cos(a)⋅cos(b)−sin(b)⋅sin(a)=cos(a)⋅cos(b)+sin(b)⋅sin(a)
2.2. 삼각 함수의 배각 정리
이 부분은 cos(2a)=cos(a+a),sin(2a)=sin(a+a)으로 치환해서 풀 수 있다.
cos(2a)sin(2a)=cos2(a)−sin2(a)=2cos2(a)−1=1−2sin2(a)=sin(a)cos(a)+sin(a)cos(a)=2sin(a)cos(a)
2.3. 삼각 함수의 극한
주요 삼각 함수(sin,cos,tan)의 극한에 대해서 구하면 아래와 같다.
x→πlimsin(x)x→4πlimcos(x)x→πlimtan(x)=sin(π)=0=cos(4π)=22=cos(π)sin(π)=0
추가로 삼각 함수의 역수(csc,sec,cot)에 대해서도 한번 짚고 넘어가자.
csc(x)=sin(x)1,sec(x)=cos(x)1,cot(x)=sin(x)cos(x)
2.4. 삼각 함수의 도함수
삼각 함수의 도함수를 구해보면, sin과 cos이 서로 관련이 있다는 재밌는 특징이 있다.
∂x∂sin(x)=cos(x),∂x∂cos(x)=−sin(x),∂x∂tan(x)=sec2(x)∂x∂csc(x)=−cot(x)csc(x),∂x∂sec(x)=tan(x)sec(x),∂x∂cot(x)=−csc2(x)
3. 미분의 다양한 공식
3.1. 곱의 미분법 (Product Rule)
f(x)=u(x)⋅v(x),f′(x)=u′(x)v(x)+u(x)v′(x)
3.2. 몫의 미분법 (Quotient Rule)
f(x)=v(x)u(x),f′(x)=[v(x)]2u′(x)v(x)−u(x)v′(x)
3.3. 합성함수의 미분법
f(x)=h(g(x)),f′(x)=h′(g(x))⋅g′(x)
3.4. 자연 로그/상수를 이용한 미분법
∂x∂[ax]=lna⋅ax,∂x∂[logax]=(lna)⋅x1
위 미분법에 대한 풀이는 아래와 같다.
∂x∂[ax]∂x∂[logax]=∂x∂[(elna)x]=∂x∂[elna⋅x]…using Chain Rule=∂lna⋅x∂[elna⋅x]⋅∂x∂[lna⋅x]=elna⋅x⋅lna=(lna)⋅elna⋅x=(lna)⋅ax=∂x∂[lnalnx]=lna1⋅∂x∂[lnx]=lna1⋅x1=(lna)⋅x1
4. 음함수의 미분
보통의 양함수 또는 명시적(Explicit) 함수는 y=f(x) 형태로 표현되지만,
음함수(Implicit Function)은 두 변수 x,y 사이의 관계로 정의되고
f(x,y)=0와 같은 형태로 표현된다.
음함수의 미분에서는 변수 y를 x에 대한 함수로 간주한 뒤 미분하여 ∂x∂y를 구한다.
4.1. 음함수의 도함수
x2+y2=1 식을 가지고 y를 x에 대해 미분하려면,
아래와 같이 양변을 모두 미분함으로써 ∂x∂y를 찾아낼 수 있다.
∂x∂[x2+y2]∂x∂[x2]+∂x∂[y2]2x+∂y∂y2⋅∂x∂y2x+2y⋅∂x∂y∂x∂y=∂x∂[1]=0=0…Composite Function=0=2y−2x=−yx
음함수의 성질
위와 같이 음함수를 미분한 결과는 양함수를 미분한 결과와 같다.
음함수 xy=1와 양함수 y=x−2는 같은 식이며, 이를 미분한 결과는 같다.
4.2. 역함수의 도함수
f(x),g(x)가 있을 때 2개의 함수가 서로 역함수라면,
g(x)=f−1(x),g(f(x)=x 이며, 도함수에서는 f′(x)=g′(f(x))1 의 관계를 가진다.
이는 아래 식을 통해 확인할 수 있다.
g(f(x))∂x∂[g(f(x))]g′(f(x))⋅f′(x)f′(x)=x=∂x∂[x]=1=g′(f(x))1
5. 매개변수 방정식의 미분
매개변수 방정식이란, 아래와 같이 어떠한 매개변수(t)를 통해 다른 함수(x,y)가 정의되는 것을 말한다.
x=2sin(1+3t),y=2t3
위와 같은 식에서 ∂x∂y를 구한다고 했을 때,
함수 x,y 모두 t에 관한 함수이기 때문에 ∂x∂y=∂t∂y÷∂t∂x 를 통해 계산할 수 있다.
∂x∂y=∂t∂2t3÷∂t∂2sin(1+3t)=6t2÷(2cos(1+3t)⋅3)=6cos(1+3t)6t2=cos(1+3t)t2
6. 이계도함수
이계도함수란, 단순히 미분을 2번 연이어 하는 것을 말하며, 아래와 같이 표기한다.
∂x2∂2y=∂x∂[∂x∂[y]]…∂x2∂26x−2=36x−4
참고로 이계도함수의 라그랑주 표기법은 f′′, 라이프니츠 표기법은 ∂x2∂2y 이다.
7. 극대/극소값
함수에서 극대값은 어떠한 구간에서 가장 큰값이고, 극소값은 가장 작은값을 의미한다.
극대값과 극소값 지점에서의 도함수(기울기) 값은 0이 나오게 되는데,
더 자세히 살펴보면 극대값 이전의 함수값은 증가하고 있고, 이후의 함수값은 감소한다.
반대로 극소값 이전의 함수값은 감소하고, 이후의 함수값은 증가함을 알 수 있다.
극대/극소값 구하기
어떠한 함수가 주어졌을때, 도함수가 0이 되는 지점을 구할 수 있는데
이를 임계점(critical point)라고 말한다.
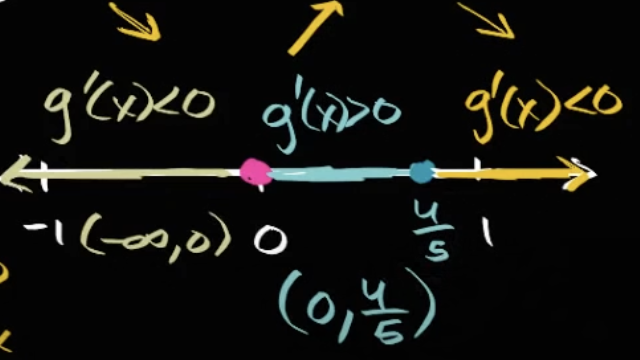
g(x)g′(x)g′(x)=x4−x5=4x3−5x4=x3(4−5x)=0⟺x=0or54
위 예제에서는 x=0or54일때 도함수의 값이 0이 되고,
2개의 지점이 임계점이라고 말할 수 있다.
다만 어떤 지점이 극대값이고 극소값인지 알기 위해서는 각 구간에서의 도함수(기울기) 값을 알아야 하는데,
아래의 그림처럼 위에서 구한 지점의 양쪽에 존재하는 임의 지점의 도함수 값을 구함으로써 알 수 있다.
8. 함수의 오목성/변곡점
8.1. 오목성(Concavity)
오목성이란, 함수의 형태가 아래로 오목거나 위로 오목한(=볼록한) 경우를 말한다.
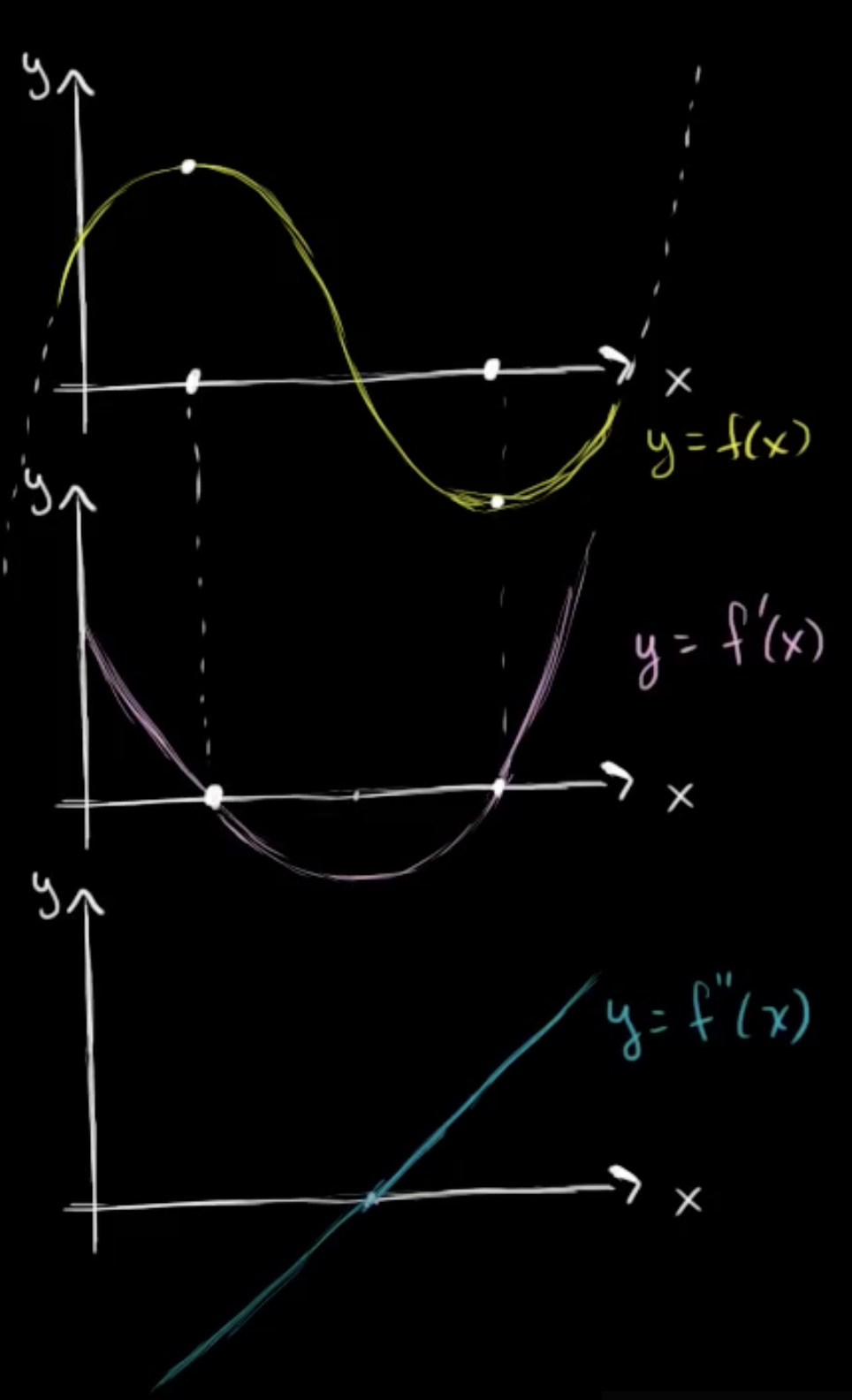
위의 그림을 보면 위에서 아래 순으로 함수, 일계도함수, 이계도함수이며
아래와 같이 서로 오목성(Concavity)에 대한 관련성을 가진다.
1️⃣ 위로 오목(Concave upwards, ≈ 볼록)
함수 f(x)에서 기울기가 점점 감소한다면,
일계도함수 f′(x) 또한 점점 감소하며 이계도함수 f′′(x)<0 이다.
2️⃣ 아래로 오목(Concave downwards)
함수 f(x)에서 기울기가 점점 증가한다면,
일계도함수 f′(x) 또한 점점 증가하며 이계도함수 f′′(x)>0 이다.
8.2. 변곡점(Inflection Point)
변곡점이란, 함수의 형태가 오목 → 볼록, 또는 볼록 → 오목으로 바뀌는 지점을 말한다.
이는 이계도함수 f′′(x)의 값이 양 → 음, 또는 음 → 양으로 바뀌는 지점이다.

