[선형대수학] 단위 벡터와 정사영

1. 단위 벡터 (Unit vector)

1. 단위 벡터의 정의
   벡터의 크기(norm)가 1인 벡터를 단위 벡터(unit vector)라고 한다.
   ※ 벡터의 크기 norm $=\, ||\vec{v}|| \,=\, \sqrt{v_1^2 + v_2^2 + \dots + v_n^2}$
2. 단위 벡터 구하기
   • 주어진 벡터 $\vec{v}$ 와 같은 방향의 단위 벡터를 $\vec{u}$ 라고 했을 때, 아래 공식을 통해서 단위벡터를 구할 수 있다.
   • 단위 벡터 $\vec{u} = \frac{1}{||\vec{v}||}\vec{v}$
   • 단위 벡터 공식의 증명
     $||\vec{u}|| = ||\frac{1}{||\vec{v}||}\vec{v}|| = ||\frac{1}{||\vec{v}||}|| \, ||\vec{v}|| = \frac{1}{||\vec{v}||} ||\vec{v}|| = 1$
3. 예시
   벡터 $\vec{v}$ 가 아래와 같이 주어졌을 때, 단위 벡터를 $\vec{u}$ 구하는 방법은 아래와 같다.
   $\vec{v} \,=\, \begin{bmatrix}1\\ 2\\ -1\end{bmatrix} \quad,\quad ||\vec{v}|| = \sqrt{1^2 \,+\, 2^2 \,+\, (-1)^2} \,= \sqrt{6} \\\,\\ \vec{u} \,=\, \frac{1}{||\vec{v}||}\vec{v} \,= \, \frac{1}{\sqrt{6}}\begin{bmatrix}1\\ 2\\ -1\end{bmatrix} \,=\, \begin{bmatrix}\frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{6}}\\ \frac{-1}{\sqrt{6}}\end{bmatrix}$

2. 정사영 (Orthogonal projection)

1. 정사영의 정의
   어떠한 도형 또는 선분 $\vec{v}$ 에 빛을 비추었을 때, 빛과 수직인 평면 $\textbf{U}$ 에 생기는 그림자를 말한다.
   이때 평면 $\textbf{U}$ 에 생기는 그림자를 $proj_{\textbf{U}}(\vec{v})$ 와 같이 표현한다.
   
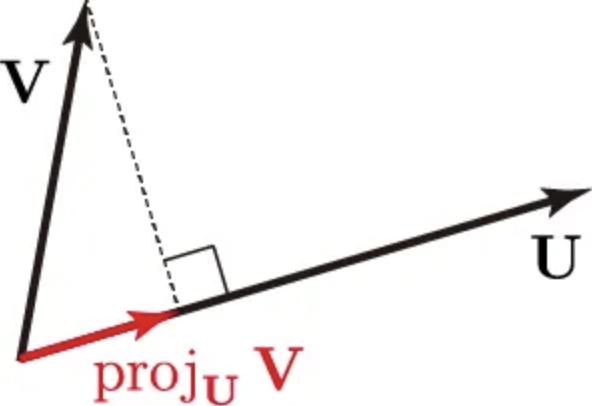
2. 정사영의 성질
   • $proj_{\textbf{U}}(\vec{v})$ 와 $\vec{v} - proj_{\textbf{U}}(\vec{v})$ 는 서로 직교하기 때문에, $proj_{\textbf{U}}(\textbf{V}) \cdot (\vec{v} - proj_{\textbf{U}}(\vec{v})) = 0$ 이다.
   • $proj_{\textbf{U}}(\vec{v})$ 는 평면 $\textbf{U}$ 와 같은 방향이기 때문에, $proj_{\textbf{U}}(\vec{v}) = c\textbf{U}(c \in \mathbb{R})$ 이다.
   • $proj_{\textbf{U}}(\vec{v})$ 는 평면 $\textbf{U}$ 와 같은 방향이기 때문에, $\textbf{U} \cdot (\vec{v} - proj_{\textbf{U}}(\vec{v})) = 0$ 이다.
3. 정사영 구하기
   위의 정사영의 성질에 따라, 다음과 같은 수식을 통해 정사영을 구할 수 있다.
   $\textbf{U} \cdot (\vec{v} - proj_{\textbf{U}}(\vec{v})) \,=\, \textbf{U} \cdot (\vec{v} - c\textbf{U}) \,=\, 0 \\\,\\ \textbf{U} \cdot \vec{v} \,-\, c\textbf{U} \cdot \textbf{U} = 0\\\,\\ \textbf{U} \cdot \vec{v} \,=\, c\textbf{U} \cdot \textbf{U}\\\,\\ \frac{\textbf{U} \cdot \vec{v}}{\textbf{U} \cdot \textbf{U}} \,=\, c \\\,\\ proj_{\textbf{U}}(\vec{v}) \,=\, c\textbf{U} \,=\, \frac{\textbf{U} \cdot \vec{v}}{\textbf{U} \cdot \textbf{U}}\textbf{U} \,=\, \frac{\textbf{U} \cdot \vec{v}}{|| \textbf{U} ||^2}\textbf{U}$
4. 예시
   벡터 $\vec{x}, \vec{v}$ 와 선분 $\textbf{L}$ 이 주어졌을 때, 다음과 같이 정사영을 구할 수 있다.
   $\vec{x} \,=\, \begin{bmatrix}2 \\ 3\end{bmatrix} \quad,\quad \vec{v} \,=\, \begin{bmatrix}2 \\ 1\end{bmatrix} \quad,\quad \textbf{L} \,=\, \big\{c\vec{v} \,|\, c \in \mathbb{R}\big\} \\\,\\ proj_{\textbf{L}}(\vec{x}) \,=\, c\vec{v} \,=\, \frac{\vec{x}\cdot\vec{v}}{\vec{v}\cdot\vec{v}}\vec{v} \\\,\\ proj_{\textbf{L}}(\vec{x}) \,=\, \frac{\begin{bmatrix}2 \\ 3\end{bmatrix} \cdot \begin{bmatrix}2 \\ 1\end{bmatrix}}{\begin{bmatrix}2 \\ 1\end{bmatrix} \cdot \begin{bmatrix}2 \\ 1\end{bmatrix}} \begin{bmatrix}2 \\ 1\end{bmatrix} \,=\, \frac{7}{5}\begin{bmatrix}2 \\ 1\end{bmatrix} \,=\, \begin{bmatrix}\frac{14}{5} \\ \frac{7}{5}\end{bmatrix} \,=\, \begin{bmatrix}2.8 \\ 1.4\end{bmatrix}$

3. 단위 벡터와 정사영

단위 벡터가 주어졌을 때, 정사영은 보다 더 간략하게 구할 수 있다.

정사영은 선형 결합의 조건을 만족하므로, 행렬과 벡터의 곱셈으로 나타낼 수 있다.