[선형대수학] 벡터의 내적과 외적

벡터의 곱하기는 2가지 종류가 있다.
벡터의 내적과 외적, 2가지 종류에 대해서 정리해보고자 한다.

1. 벡터의 내적

• 내적(dot product) : 벡터의 방향을 고려하여 수처럼 곱하는 방식이며, 기호 $\cdot$ 를 사용하고 결과는 스칼라이다.
• 교환 / 결합 / 분배 법칙의 적용이 가능하다.
• 벡터의 내적은 다음과 같이 계산한다.
  $\vec{a} \cdot \vec{b} = \begin{bmatrix} a_1 \\ a_2 \\ \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \end{bmatrix} = a_1b_1 + a_2b_2$
• 벡터 간 각도를 통해서 다음과 같이 계산할 수 있다.
  2개 벡터가 서로 수직이라면, 내적의 값은 0이다. ( $cos90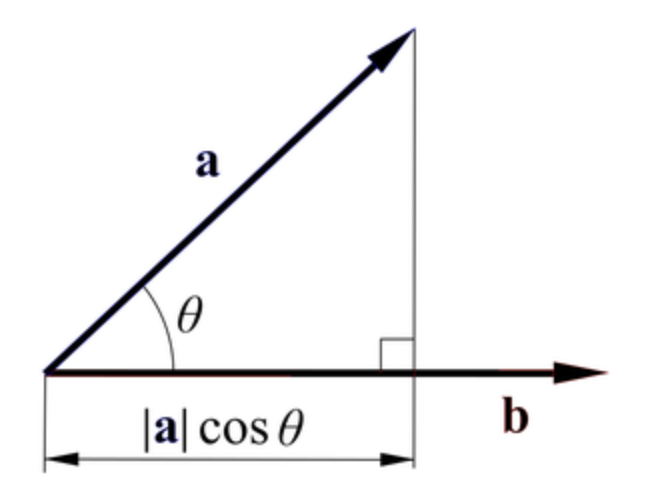^\circ$ = 0 )
  $\vec{a} \cdot \vec{b} = ||\vec{a}|| \, ||\vec{b}|| \, cos\theta$
  

1.1. 벡터의 길이(norm)

• 벡터의 길이(또는 크기, norm)는 스칼라 값으로 표현된다.
• $\vec{v}$ 의 길이는 $|| \vec{v} ||$ 와 같이 표현하며 다음과 같이 계산한다.
  $|| \vec{v} || = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}$
• 벡터의 길이는 벡터 스스로를 내적한 뒤 제곱근 한 결과와 같다.
  $|| \vec{a} || = \sqrt{\vec{a} \cdot \vec{a}}$

1.2. 코시-슈바르츠 부등식

• $|| \vec{x} \cdot \vec{y} || \le || \vec{x} || \, ||\vec{y}||$
• $|| \vec{x} \cdot \vec{y} || = || \vec{x} || \, ||\vec{y}|| \iff \vec{x} = c\vec{y}\quad$ ($\vec{x}$, $\vec{y}$ 가 선형 종속인 경우)

2. 법선 벡터

• 평면에 대한 수직인 벡터를 법선 벡터라고 한다.
• $ax + by + cz = d$ 로 정의된 평면에서,
  $\vec{n} = [a, b, c]$ 는 평면 내의 벡터와 직교하는 방향을 가리키는 법선 벡터이다.

2.1. 평면과 법선 벡터의 관계

• 평면 내의 벡터와 법선 벡터의 내적
  법선 벡터 $\vec{n}$ 와 평면 내의 벡터 $\vec{a}$ 을 내적하면 값은 0이다.
  $\vec{n} \cdot \vec{a} = ||\vec{n}|| \, ||\vec{a}|| \, cos\,\theta = 0 \quad \dots \quad (\theta = 90^\circ, cos\,\theta = 0)$
• 법선 벡터를 통한 평면 방정식 유도
  원점으로부터 평면 내의 점 $a(x, y, z)\,,\,p(1, 3, 2)$ 를 가르키는 벡터 $\vec{a} \,,\,\vec{p}$ 가 있다고 가정했을때,
  법선 벡터 $\vec{n}$ 와 평면 내의 벡터 $\vec{a} - \vec{p}$ 를 내적하면 0이 나옴을 통해 평면 방정식을 유도할 수 있다.
  $\vec{n} = \begin{bmatrix} 2 \\ 3 \\ 4 \\ \end{bmatrix}\quad , \quad \vec{a} - \vec{p} = \begin{bmatrix} x-1 \\ y-3 \\ z-2 \\ \end{bmatrix} \\ \vec{n}\,\cdot\,(\vec{a} - \vec{p})\,=\,2(x-1) + 3(y-3) + 4(z-2) = 0 \\ \quad\quad\quad\quad\,= 2x + 3y +4z + (-2 - 9 - 8) = 0 \\ = 2x + 3y +4z = 19\quad\quad\,\, \\ : Ax + By + Cz = D\quad\;\;\;$
• 점과 평면 사이의 거리
  평면 방정식 $Ax+By+Cz=D$ 와 임의의 점 $P (x_p, y_p, z_p)$ 가 주어졌을 때,
  점과 평면 사이의 최단 거리 $d$ 는 다음과 같이 구할 수 있다.
  $d = \frac{Ax_p+By_p+Cz_p-D}{\sqrt{A^2+B^2+C^2}}$

3. 벡터의 외적

• 외적(cross product) : 3차원에서의 2개 벡터에 대해 직교하는 벡터를 구할 수 있다. 기호 $\times$ 를 사용하고 결과는 벡터로 나온다.
• 벡터의 외적은 다음과 같이 계산한다.

• 벡터 간 각도를 통해서 다음과 같이 계산할 수 있다.
  $||\vec{a} \times \vec{b}|| = ||\vec{a}|| \, ||\vec{b}|| \, sin\theta$
• $\vec{a}\times\vec{b}=\vec{c}$ 이라면,  $\vec{a}\cdot\vec{c}=\vec{b}\cdot\vec{c}=0$ 이다.
  외적은 주어진 벡터들과 직교하는 벡터를 구하기 때문에, 주어진 벡터와 내적을 하게 되면 0이 된다.

3.1. 벡터의 내적과 외적의 비교

• 내적
  • $\vec{a}\cdot\vec{b}$ 의 결과는, $\vec{a}$ 에서 $\vec{b}$ 방향으로 향하는 일부와 $||\vec{b}||$ 를 곱한 값을 의미한다.
  • 2개 벡터가 같은 방향으로 향하는 정도를 구한다.
• 외적
  • $\vec{a}\times\vec{b}$ 의 결과는, $\vec{a}$ 에서 $\vec{b}$ 방향으로 수직하는 값과 $||\vec{b}||$ 를 곱한 값을 의미한다.
• 내적은 $\theta$ 가 $0^\circ$ 일 때 최댓값을 가지고, $90^\circ$ 일 때 0을 가진다. $[\,cos(0^\circ)=1,\,cos(90^\circ)=0\,]$
  외적은 $\theta$ 가 $90^\circ$ 일 때 최댓값을 가지고, $0^\circ$ 일 때 0을 가진다. $[\,sin(0^\circ)=0,\,sin(90^\circ)=1\,]$

3.2. 외적과 평행사변형

• 주어진 벡터의 외적값은 주어진 벡터로 이루어진 평행사변형의 넓이와 같다.
  $\vec{a}\times\vec{b} = \vec{a},\,\vec{b}$ 로 이루어진 평행사변형의 넓이
• 증명
  $평행사변형의\;넓이=밑변 \times 높이 = ||\vec{a}||\times h\\ sin\theta=\frac{h}{||\vec{b}||}\quad\cdots\quad h=||\vec{b}||\,sin\theta\\ \,\\ 평행사변형의\;넓이 = ||\vec{a}||\times h = ||\vec{a}||\,||\vec{b}||\,sin\theta = ||\vec{a}\times\vec{b}||$
  

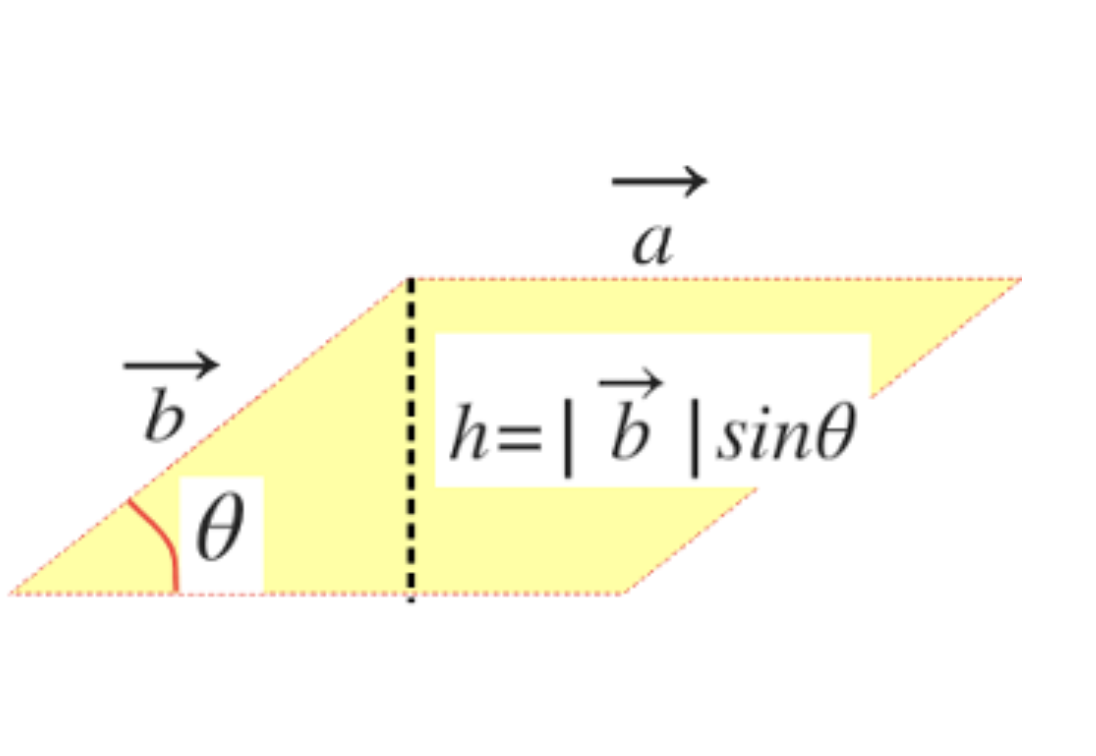
4. 기약 행사다리꼴 행렬을 이용한 연립방정식 풀이

4.1. 기약 행사다리꼴 (Reduced Row Echelon Form, RREF)

• 성립 조건
  1. 0이 아닌 원소를 갖는 행에서 맨 처음 나오는 0이 아닌 수는 1이어야 한다.
     (이러한 1을 leading 1이라고 한다.)
  2. 0이 아닌 원소를 갖는 연속된 두 행은 해당 행의 leading 1이 윗 행의 leading 1보다 오른쪽에 있어야 한다.
  3. 모든 원소가 0인 행은 행렬의 맨 아래로 내려가야 한다.
  4. leading 1이 있는 열의 나머지 원소들은 모두 0이어야 한다.
• 기약 행사다리꼴 행렬 변환 예시
  leading 1을 다른 말로 pivot entry, pivot variable 이라고 표현할 수 있고,
  leading 1이 아닌 변수를 free entry, free variable 이라고 표현할 수 있다.
  $\quad\quad\textbf{A} = \begin{bmatrix} 1 & 2 & 1 & 1 \\ 1 & 2 & 2 & -1 \\ 2 & 4 & 0 & 6 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 1 & 1 \\ 0 & 0 & 1 & -2 & ... & R2-R1 \\ 0 & 0 & -2 & 4 & ... & R3-2R1 \end{bmatrix} \\$
  $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad= \begin{bmatrix} 1 & 2 & 0 & 3& ... & R1-R2\\ 0 & 0 & 1 & -2\\ 0 & 0 & 0 & 0 & ... & R3+2R2 \end{bmatrix} \\$
  $RREF(\textbf{A}) = \begin{bmatrix} 1 & 2 & 0 & 3 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0 \end{bmatrix}$

4.2 행사다리꼴 (Row Echelon Form, REF)

• 성립 조건
  • 기약 행사다리꼴의 성립 조건 1~3번만을 만족하는 행렬
• 행사다리꼴 행렬 예시
  $\begin{bmatrix} 1 & 5 & 8 & -6 \\ 0 & 1 & 4 & 2 \\ 0 & 0 & 1 & 5 \end{bmatrix}\;,\; \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}\;,\; \begin{bmatrix} 0 & 1 & 6 & 3 & 0 \\ 0 & 0 & 1 & -9 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}$