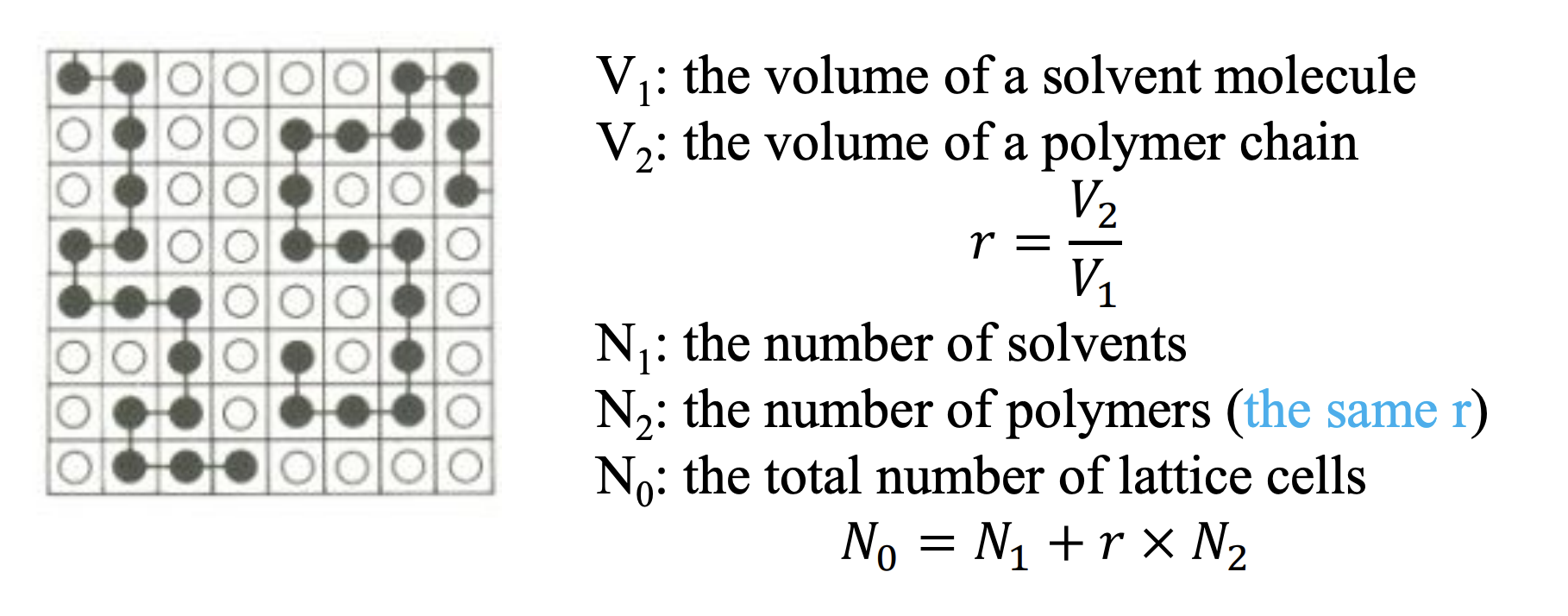Introduction

열역학에서 enthalpy와 entropy를 고려하여 Gibbs free energy, $G$는 다음과 같이 나타낸다.

그럼 2개 system을 섞는다고 가정하면, 섞은 후의 $G$와 섞기 전의 $G$의 차이인 $\Delta G_M$는 다음과 같다.

이 때 homogeneous solution은 $\Delta G_M < 0$이여야 얻을 수 있을 것이다. 이번 시간에는 small molecules의 mixing은 열역학적으로 어떻게 구했는 지 알아보고 polymer의 경우에는 small molecules의 mixing 식이 아닌 다른 식이 유도되는 이유와 과정을 Flory-Huggins Theory를 통해 알아보고 polymer solution의 깁스 자유 에너지 변화량을 나타내는 Flory-Huggins equation에 대해 배워보자.

Ideal Mixing

polymer mixing을 알아보기 전에 small molecules의 ideal mixing을 우선 알아보자. 우선 ideal하다는 의미는 분자 간의 상호작용이 분자의 종류에 무관하기에 오직 entropic effect만 고려하겠다는 의미와 서로를 당기거나 밀어내는 intermolecular force가 동일하다는 것이다. 이 때 우리는 열역학적 정의에 의한 entropy의 정의를 사용할 것이다. 이는 이전 시간에 배웠듯이 다음과 같다.

Assumptions

ideal mixing이기에 몇 가지의 가정을 고려하자. 이는 다음과 같다.

1. 두 분자를 섞었을 때, 부피의 변화가 없다. 즉, $\Delta V_m = 0.$
2. 분자들의 크기는 동일하다.
3. entropic effect만 고려하기에, enthalpy의 변화가 없다. 즉, $\Delta H_m = 0.$
4. 평형 위치에 대한 component의 움직임은 섞은 후에도 변하지 않는다.

Configurational Entropy

엔트로피를 $\Omega$, 경우의 수로 설명하기에 이를 알아보자. 우선, 섞기 전에는 component(molecules)간의 가능한 경우의 수는 1이다.

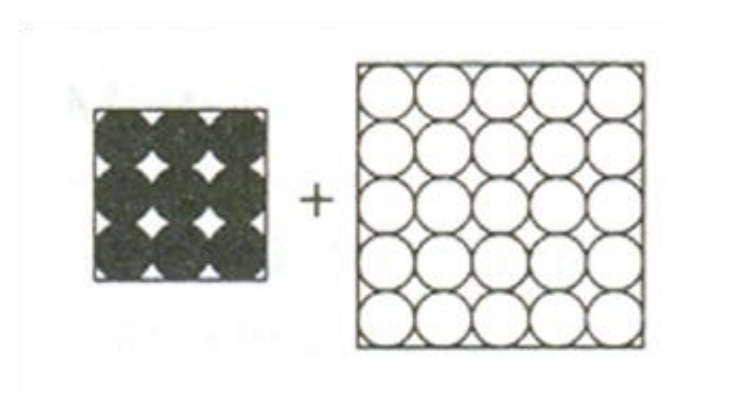
그럼 섞은 후에는 어떻게 될까? $N_1 + N_2 \equiv N_0$라 하자. 그럼 이 때, component의 가능한 경우의 수 $\Omega$는 고등 수학 때 배운 조합을 떠올려보면, 다음과 같다.

이렇게 섞은 후의 경우의 수를 고려하여 mixing 후의 구성(공동 구조)를 가정한 entropy를 configurational entropy($S_c$)라고 한다. $\Omega$를 그대로 $S$에 대입해주면,

Approximation

Stirling's Approximation : $\ln N! = n\ln N - N$

위 과정을 이용하면, configurational entropy는 다음과 같다.

$\Delta S$ and $\Delta G$ for mixture

섞기 전 가능한 경우의 수는 1이였으므로, component $i$에 대한 경우의 수는 $S_i = k \ln 1 = 0$이다. 섞은 후의 엔트로피는 configurational entropy, $S_c$라 하였다. 그러므로 $\Delta S_{ideal}^{M}$은 다음과 같다.

여기서 mole fraction을 사용하여, $x_i = \frac{N_i}{N_0}$라 하면,

만약, 단위 lattice 당 ideal mixture의 entropy의 변화량을 알고 싶다면, 전체를 $N_0$로 나누어 주면 된다. 이는 다음과 같다.

Gibbs free energy의 정의에 의해 ideal mixture의 깁스 자유 에너지의 변화량은 다음과 같다.

Flory-Huggins Theory

Polymer chain

우리가 알고 싶은 것은 small molecules가 아닌 polymer chain의 mixing이다. polymer chain은 chian connectivity가 존재한다. 즉, component를 이루는 monomer가 연결되어 있다. 그렇기에 다음 그림과 같은 양상을 띄게 된다.

이런 chain connectivity를 고려한 polymer mixing을 다룬 이론이 바로 Flory-Huggins theory이다. 우선 고분자 chain은 mixing에 의한 열의 발생이 존재한다. 이는 enthalpy에 해당한다. 또한 앞서 설명한 chian connectivity에 의한 고분자와 solvent molecules 사이의 크기의 큰 차이가 존재한다. 이것은 entropy에 영향을 줄 것이다. 즉, chain connectivity는 polymer solution에서 entropy 변화량이 lattice 내에 solvent와 polymer chain을 배치하는 경우의 수가 되게 한다.

Polymer mixing

lattice 내의 components와 component를 구성하는 molecule을 통해 경우의 수를 구하기 위해 다음과 같은 변수를 정의하자.

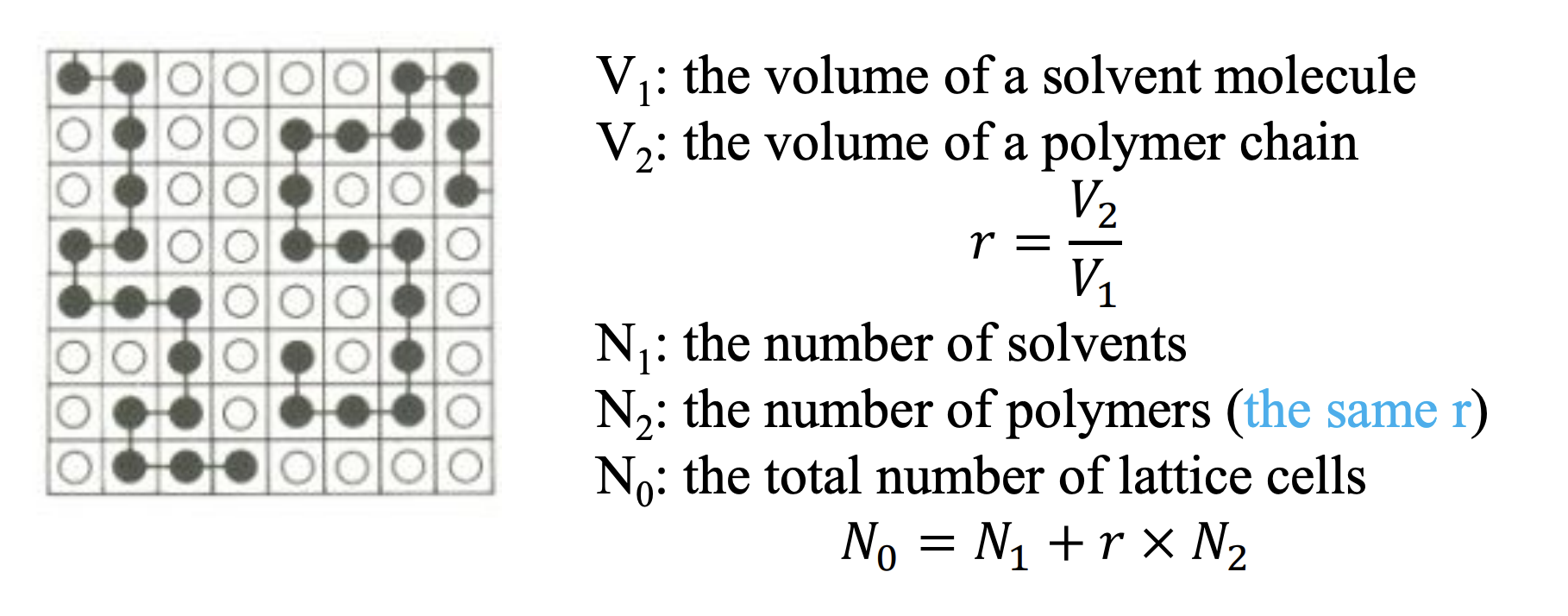
만약 $i$개의 polymer가 이미 lattice 내에 존재한다고 하자. 이 때 $(i+1)$번째 polymer가 lattice 내에 추가된다고 하면, $r\times i$의 cell들은 고분자들이 lattice 내부에 차지하고 있을 것이다. 그럼 이 때 $(i+1)$번째 polymer의 첫번째 segment가 lattice 내부에 존재할 수 있는 경우의 수는

가 된다. 두번째 segment는 첫번째 semgent의 옆에 놓일 수 있는 경우의 수가 될 것인데, 여기서 인접한 cell이 비어 있을 확률을 $p_i$라 하자. $p_i$는 다음과 같다.

그리고 $z$를 첫번째 segment에 인접한 cell의 수라 하자. 그럼 두번째 segment가 lattice 내부에 가능한 경우의 수는

세번째 그리고 그 이후의 segment에 대한 경우의 수는

라 하자. 그럼 $(i+1)$번째 고분자가 lattice에 올 수 있는 전체 경우의 수($w_i$)는 다음과 같다. 이 때 $(i+1)^{th}$ 고분자는 $r$개의 segment를 가진다.

마지막에 $z$를 $z-1$로 근사한 것이다. 위 식을 통해 lattice내에 존재하는 모둔 $N_2$ 고분자들이 lattice에 존재할 수 있는 전체 경우의 수는 다음과 같을 것이다.

$N_2$개의 고분자들이 전부 동일하다면(identical), 경우의 수를 따질 때 중복의 경우를 제거해야 하므로, 다음과 같다.

$w_p$를 계산하기 위해 위에서 구한(근사) $w_{i+1}$를 통해 $w_i$를 나타낼 수 있다. 계산 과정은 생략하도록 하자. 최종적으로 얻은 $w_p$의 결과는 다음과 같다.

이제 섞은 후의 entropy $S^M$을 구해보자.

여기서 $\ln x! = \ln (x/e)^x$라는 가정을 사용하자. 그럼 다음과 같이 전개 된다.

Entropy of Polymer Mixture

이제 $\Delta S^M$을 구하기 위해, 섞기 전을 가정해보자. 섞기 전에는 pure solvent와 pure polymer만 존재할 것이다. 각각의 entropy를 위 식을 이용하여 구해보면 다음과 같다. pure solvent는 $N_2 = 0$인 경우이므로,

pure polymer는 $N_1 = 0$이므로,

그럼 $\frac{\Delta S^M}{k}$는 다음과 같다.

여기서 mole fraction을 $\varphi$라 하자. 그럼 위 식은

볼츠만 상수 $k$는 기체 상수 $R$을 아보가드로 수로 나눈 값이므로, 위 식의 양변에 아보가드로 수($N_{avo}$)를 곱해주면,

단위 개수(lattice의 개수)당 polymer mixture의 엔트로피 변화량은 어떻게 구할 수 있을까? 우선 $N_1$의 정의를 다시 살펴보자. solvents의 개수이다. 그렇기에 전체 부피에 solvent의 몰 분율인 $\varphi_1$을 곱한 것이 solvent molecule 하나의 부피가 된다. 이 값으로 solvent의 전체 부피인 $V_1$을 나누어 주면 $N_1$이 나올 것이다. 이는 polymer chains의 경우에도 동일할 것이고, 최종적으로 다음이 성립한다.

polymer mixture의 엔트로피 변화량 식에 위 식을 대입해주면 다음과 같다.

그리고 $V/V_0$는 $N$의 정의를 떠올려보면, $N_0$로 쓸수 있기에 다음과 같다.

그럼 최종적으로 단위 개수당 polymer mixture의 엔트로피 변화량인 $\Delta \bar{S}^M$은 다음과 같다.

위 식을 이용해 3가지 경우의 polymer mixture의 엔트로피 변화량을 구할 수 있다.

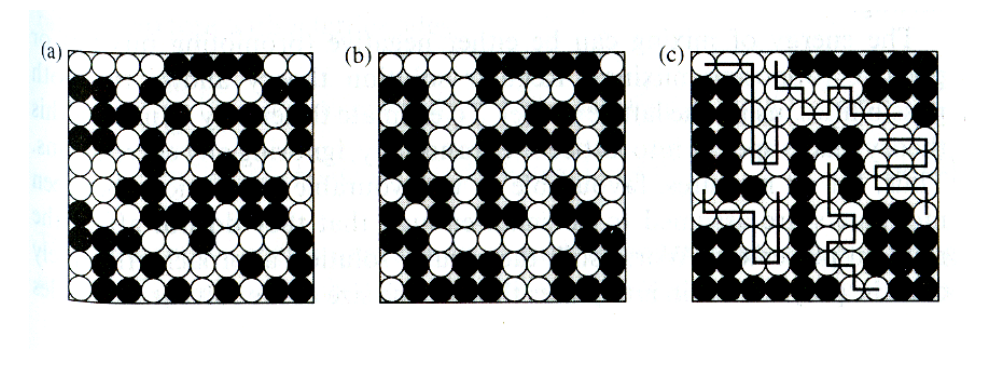
1. (c) polymer blend
   $\frac{\Delta \bar{S}^M}{k} = -\left(\frac{\varphi_1}{r_1}\ln \varphi_1 + \frac{\varphi_2}{r_2}\ln \varphi_2 \right)$
2. (b) polymer solution
   $\frac{\Delta \bar{S}^M}{k} = -\left(\varphi_1\ln \varphi_1 + \frac{\varphi_2}{r_2}\ln \varphi_2 \right)$
3. (a) regular solution
   $\frac{\Delta \bar{S}^M}{k} = -\left(\varphi_1\ln \varphi_1 + \varphi_2\ln \varphi_2 \right)$

Gibbs Free Energy of Ideal Mixture

ideal 한 경우이기에 섞기 전/후의 interaction energy(enthalpy)의 변화가 없다. 그러므로, 깁스 자유 에너지의 변화량은 다음과 같다.

자연로그 안의 값인 $\varphi$가 분율임을 생각해보면, 항상 음수가 된다는 것을 알 수 있다. 하지만 위에서 고려한 3가지 경우(polymer blend / polymer solution / regular solution)의 solution이 mixing이 선호되는 정도는 다르다. 에너지가 최소가 되어야 자발적으로 mixing이 이루어진다. 3가지 경우를 깁스 자유 에너지 식으로 plot한 결과는 아래와 같다.

plot의 결과로 polymer blend가 가장 mixing 되기 힘들고, regular solution의 경우가 가장 잘 mixing이 이루어질 것이라 예상할 수 있다.

Enthalpy of Mixture

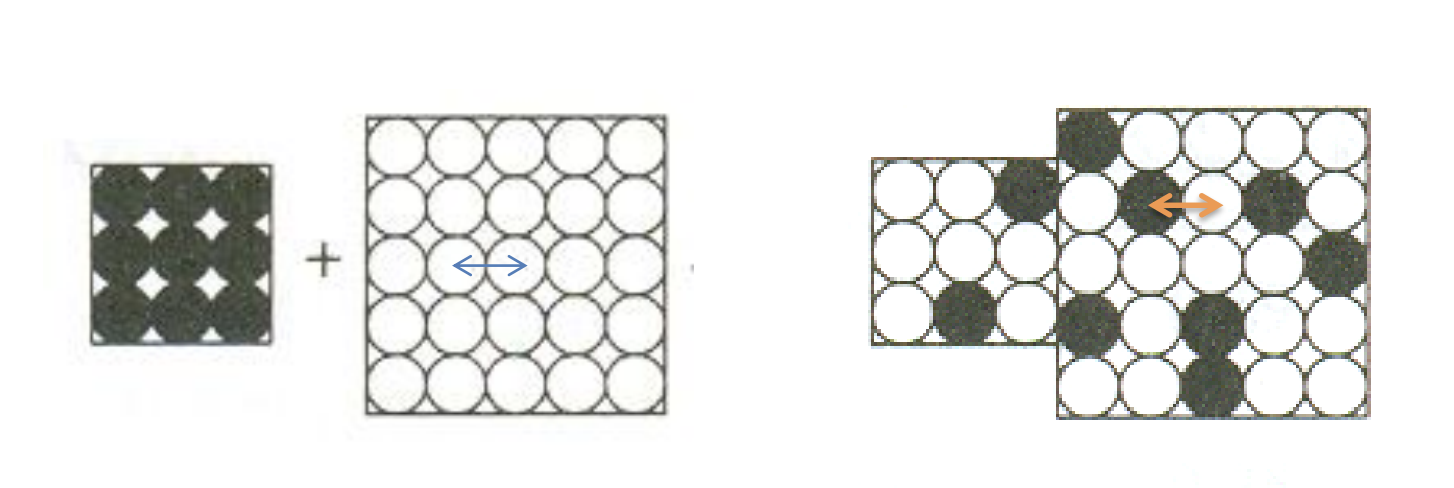
이전 chapter에서 excluded volume에 대해 배울 때, interaction energy가 enthalpy로 계산된다고 배웠다. 그렇다면 위 그림과 같은 검은색과 흰색의 lattice를 섞기 전에는 서로 다른 종끼리만 존재하기에 검은색 종의 interaction과 흰색 종의 interaction만 존재한다. 하지만 섞게 되면 검은색과 흰색 종 사이의 interaction이 새롭게 추가된다.

만약 고분자와 solvent species 사이의 interaction을 고려해본다면, 여기서 1을 polymer species, 2를 solvent species라고 하자. 그럼 서로 다른 종끼리의 충돌/접촉 시 발생하는 에너지를 계산해보자. 고분자와 고분자 간의 충돌/접촉 시 발생하는 에너지를 $\varepsilon_{11}$, solvent와 solvent 간의 에너지를 $\varepsilon_{22}$, 고분자와 solvent 간의 에너지를 $\varepsilon_{12}$라고 하자. 섞기 전과 섞은 후의 고분자와 solvent 간의 접촉 시 발생하는 에너지의 차이 $\Delta \varepsilon_{12}$를 구해보자. 그럼 다음과 같다.

Enthalpy for a polymer chain

이제 고분자 chain 안에 존재하는 monomer를 고려해보자. 이때 우리는 인접 lattice cell에 solvent molecule가 위치할 확률을 고려해주어야 한다. 이 확률을 $\phi_1$이라 하자. 위 정의에 따라 mixing 전/후의 enthalpy의 변화량, $\Delta H_m$은 $\Delta \varepsilon_{12}$로 간주할 수 있었다. 하지만 지금 우리는 단순한 저분자 물질1, 2간의 mixing이 아니라 1이 solvent 2가 polymer chain인 경우를 가정한다. lattice cell model에서 polymer-solvent species의 접촉은 인접한 lattice cell에 solvent molecule이 위치할 확률 $\phi_1$에 의해 계산된다. 그리고 $\Delta \varepsilon_{12}$는 한 번의 서로 다른 종의 접촉에 의해 발생한다.

그러므로, 접촉 횟수를 $q$라고 하면, "한 개의" polymer chain의 섞은 후의 엔탈피 변화량, $\Delta H_m$은 $q\Delta\varepsilon_{12}$로 계산된다.

여기서 $q$는 위에서 설명했듯이, lattice model에서 solvent molecule이 polymer chain의 monomer의 인접 lattice cell에 위치할 확률 $\phi_1$에 의해 계산된 polymer-solvent 사이의 충돌/접촉 횟수이다. 각 monomer는 lattice model에서 비어 있는 cell의 개수를 $z$라고 하면, $\phi_1 z$개의 solvent molecules로 둘러싸인다. 그렇다면 polymer chain 하나는 solvent molecules로 $\phi_1 z r$개의 solvent molecules로 둘러싸인다. 그러므로 $q = \phi_1 r z$가 되고, 최종적으로 enthalpy의 변화량은 다음과 같다.

Enthalpy for polymer chains

이제는 $N_2$개의 polymer chian를 섞게 된 후의 enthalpy 변화량을 구해보자. 다를 것은 없고 위에서 구한 polymer-solvent 사이의 충돌/접촉 횟수인 $q$에 $N_2$를 단순히 곱해주기만 하면된다.

lattice model에서 $N_1, N_2$는 전체 lattice 중 1번째 종(solvent)와 2번째 종(polymer)가 차지하는 lattice cell의 개수이고, $\phi_1, \phi_2$는 각 종의 부피 분율(volume fraction)이다. 이를 고려하면($r$은 $V_2/V_1$이였다.), 다음과 같은 식이 성립한다.

위 식을 $\Delta H^M$에 대입해주면,

여기서 1몰 당 엔탈피의 변화량을 구하고 싶다면, 양변을 $N_0$로 나누어 주면 된다.

$\chi_1$

갑자기 $\chi_1$이라는 물리량이 등장했다. 우리는 고분자와 용매 분자 간의 상호작용 에너지를 $\varepsilon_{12}$로 나타냈었다. Flory-Huggins Theory에서 $\chi$는 고분자와 용매 사이의 비이상적인 거동을 나타내는 매개변수로, 통계 역학 이론을 통해 계산된다.

로 구해지며, $k, T$는 각각 볼츠만 상수와 절대온도이다. 그렇기에 polymer solution에서 $\Delta H^M$을 구할 때, $z\Delta\varepsilon_{12} = kT\chi_1$라는 식이 등장했다.

그렇다면, $\chi$가 왜 비이상적인 거동을 나타낼까? 서로 다른 종의 이상적인(ideal)한 경우에는 섞기 전 서로 다른 두 종 사이의 interaction energy의 평균이 섞은 후 두 종 사이에서 발생하는 interaction energy와 같을 것이다.

이렇게 되면, 다음이 성립한다.

흡열 반응($\Delta H > 0$)인 경우는 다음과 같다.

이렇게 되면, 다음이 성립한다.

발열 반응($\Delta H < 0$)인 경우는 다음과 같다.

이렇게 되면, 다음이 성립한다.

열역학적 관점에서는 자발적인 mixing은 $\Delta H < 0$인 발열 반응에서 잘 이루어지기 때문에, $\Delta\varepsilon_{12}, \chi$가 0보다 작은 경우 mixing이 잘 일어난다고 볼 수 있다.

Gibbs Free Energy of Polymer Solution

깁스 자유 에너지의 정의에 의해 다음과 같다.

이 식에 Florry-Huggins의 lattice model로 유도된 enthalpy term과 entropy term을 대입해주면 다음과 같다.

고분자 용액(polymer solution)의 경우에는, $r_1 = 1$이므로

이다. 위 식이 바로 Flory-Huggins Equation이다.

$\text{F-H}$ equation에서 $\phi_2$는 부피 분율이므로 1보다 항상 작다. 그러므로 위 식에서 $\ln$을 포함하는 항들은 전부 음수가 된다. 그러므로 엔탈피와 관련된 항인 $\chi$를 포함한 항은 $\chi$ 값에 따라 음수일수도 양수일수도 있다.

Limitation of Flory-Huggins Theory

Flory-Huggins theory는 엔탈피와 엔트로피의 계산에서 lattice model을 가정하였다. 하지만 lattice model에서 lattice cell은 전부 uniform한 밀도를 갖는다고 가정했다. 또한 섞은 후의 부피 변화가 없다고 가정했으며, 고분자가 mixing되면서 발생하는 배열(arrangement)를 고려하지 않았다. 또한 고분자와 용매 사이의 interaction을 의미하는 매개변수 $\chi$는 구성(composition)을 반영하지 않는 독립적인 변수이다. 가장 중요한 점은 엔트로피의 계산에서 segment가 위치하게 될 때를 온전히 확률로 계산했다. 그렇기에 완전히 random한 경우로 $\Delta\varepsilon_{12} = 0$일 때, 위 계산이 맞아떨어진다. 그러므로 실제 mixing에서 발생하는 여러 interaction을 고려하지 않은 combinational entropy를 구한 것이다.

Non-Combinational entropy contribution

이제 이상적인 경우를 상정한 combinatorial entropy가 아닌 실제 interaction의 경우를 고려한 non-combinatorial entropy를 고려해보자. 이상적이지 않은 경우이므로 segment가 위치할 수 있는 경우의 수가 더 줄어들게 될 것이므로, entropy term도 마찬가지로 감소할 것이다. 즉, non-combinatorial entropy $\Delta S^M$는 combiational entropy보다 더 감소하게 된다. 하지만 non-combinational entropy를 직접 구하기엔 복잡하기에 다음 과정을 통해 non-combinatorial contribution을 반영한다.

non-combinatorial entropy는 Flory-Huggins theory에서 이상적인 경우를 가정하고 구한 combinatorial entropy보다 더 작은 값을 갖게 된다. 그러므로 polymer solution의 깁스 자유 에너지의 변화량, $\Delta G^M$은 증가하게 된다. 그렇다면, non-combinatorial entropy를 직접적으로 계산하지 않고, enthalpy term의 $\Delta H^M$이 $\chi_S$라는 값에 의해 증가한다고 가정하자.

즉, enthalpy term은 $\chi_1$이라는 값과 관계가 있으므로 기존의 polymer-solvent의 interaction enenrgy($\varepsilon_{12}$)로 구한 $\chi$값 $\chi_H$라고 하고, non-combinatorial의 경우에서 실제 가능한 segment의 경우의 수가 감소로 인한 entropy term의 감소로 이를 완충하기 위해 $\chi_S$항이 추가된 것이다. 이는 다음과 같이 쓸 수 있으며,

$\chi_1$에 대해 정리하면, 다음과 같다.

여기서 $\Delta\varepsilon_{12, S}$을 포함한 항은 $T$를 포함하고 있지 않다. 즉 온도에 대해 독립적인 항임을 의미한다. 간략하게 표현하면,

가 된다.