Introduction

Flory-Huggins theory에서 Flory는 통계역학을 기반으로 lattice model을 사용하여, $\Delta H, \Delta S$를 구하여 polymer solution의 $\Delta G^M$을 구하였다. 열역학적으로 자발적인 mixing은 $\Delta G <0$인 경우이다. 이전 시간에 $\Delta S^M < 0$라는 사실은 배웠다. 그리고 $\Delta H^M$은 $\chi$라는 값에 따라 음이 될 수도 양이 될 수도 있다고 배웠다. $\chi$는 고분자와 용매 사이의 비이상적인 거동을 나타내는 매개변수로, 고분자 혼합물의 상 거동(phase behavior)을 예측하는데도 사용된다.

상(phase)이란 무엇일까? 물리적, 화학적 특성이 균일한 계를 의미한다. 상평형(Phase Equilibrium)은 1개 이상의 상이 존재하는 계의 평형, 즉 시간에 따라 상의 특성이 변하지 않는 것을 뜻한다. 상평형에는 다음과 같이 3가지 상태가 존재한다.

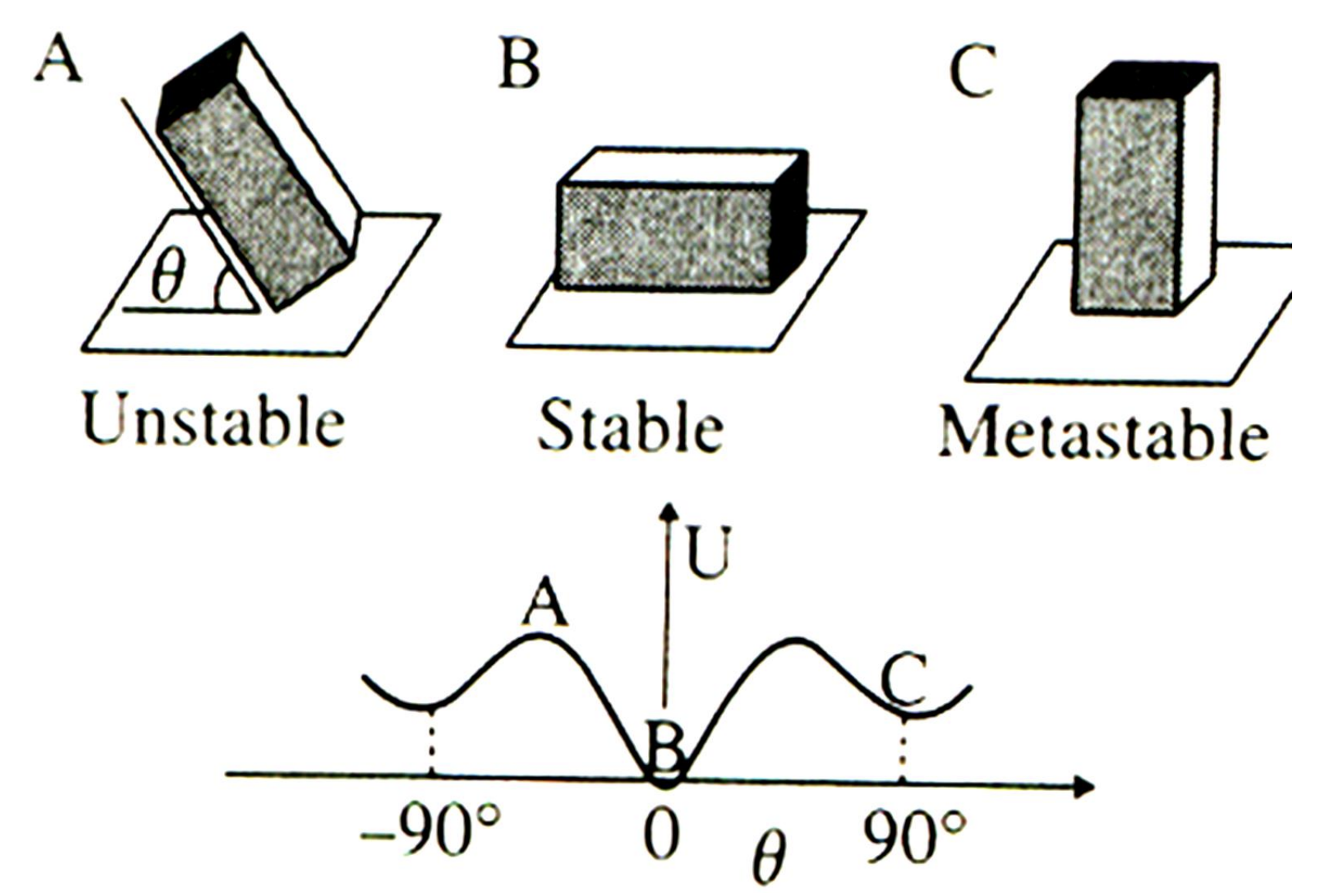
B의 경우가 가장 안정적이기에 내부 에너지는 매우 낮고, 존재할 확률이 가장 높을 것이다. C는 그 다음으로 안정적인 상태로 내부 에너지는 B보다는 좀 더 높고, 존재할 확률도 B보다는 좀 더 낮다. A는 불안정한 상태로 내부 에너지가 크고, 존재활 확률이 가장 낮다.

Complete mixing & Phase separation

두 물질을 섞을 때, 완전히 잘 섞이는 경우도 있지만, 물과 기름처럼 상의 분리가 일어나는 경우도 존재한다. 이때 두개의 상을 각각 $\alpha, \beta$ phase라고 하자. 주의할 점은 두 phase 모두 어느 한 물질만으로 구성되지 않는다는 것이다. 앞에서 상평형을 배우며 구분되는 각 상태에서 안정성($\theta$)를 내부 에너지($U$)와 연관지어 그래프로 나타냈었다. 가장 안정적인 상태가 결국 내부 에너지가 가장 낮고, 존재할 확률이 가장 크다고 했었다. 고분자의 혼합물의 경우에는 어떻게 될까? 고분자의 합성에서도 100% 섞이는 것은 매우 어렵다. 그러므로, 고분자 혼합액에서 pure한 polymer를 얻기 위해 정제를 이용한다. 정제 과정에서 $\alpha$ phase와 $\beta$ phase로 용액은 상 분리가 일어나게 되지만, 앞에서 이야기 했듯, 분리가 된 각 상에서 어느 한 물질만 100% 존재하지 않는다. 상 분리도 결국 에너지가 가장 낮은, 안정적인 상태에서 일어날 것이기 때문이다.

Energy Curve

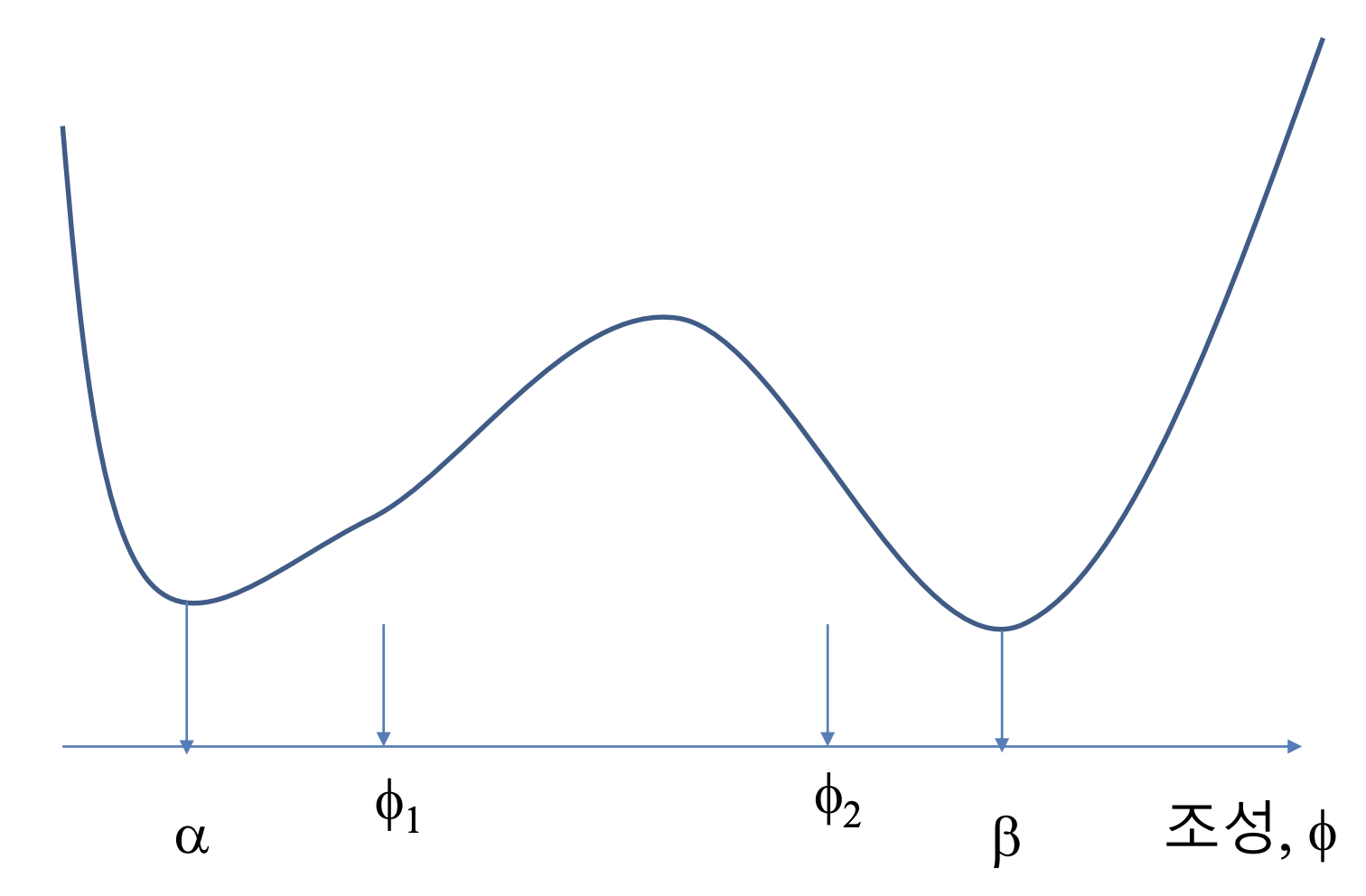
위 그래프는 두 종류의 고분자를 섞은, 고분자 혼합 용액의 energy를 조성, $\phi$에 따라 나타낸 그래프이다. 여기서 energy라고 함은 깁스 자유 에너지(Gibbs free energy)를 의미한다. 깁스 자유 에너지는 이전 시간에 다음과 같다고 배웠다.

위 식에서 $\Delta \bar{G}^M$을 $y$축으로 $\phi_1$이나 $\phi_2$를 $x$축 변수로 두고, plot하면 위와 같은 그래프를 얻을 수 있다. 여기서 $\chi$값은 이전 시간 마지막에 배웠던 근사값인 0.34를 사용해보자. 또한 $\phi_1$을 기준으로 plot한다면, $\phi_2 =(1-\phi_1)$로 두고 그리면 된다. 간단하게 표현해보면, 다음과 같은 식으로 나타나게 된다.

위 energy curve로 알 수 있는 것은 $\alpha, \beta$지점에서 상 분리가 일어나므로, 그 때가 가장 에너지가 낮은, 안정한 상태임라는 사실이다.

또한 고분자 혼합 용액의 energy curve는 온도가 올라감에 따라, 단순한 아래로 볼록한 그래프로 나타난다.

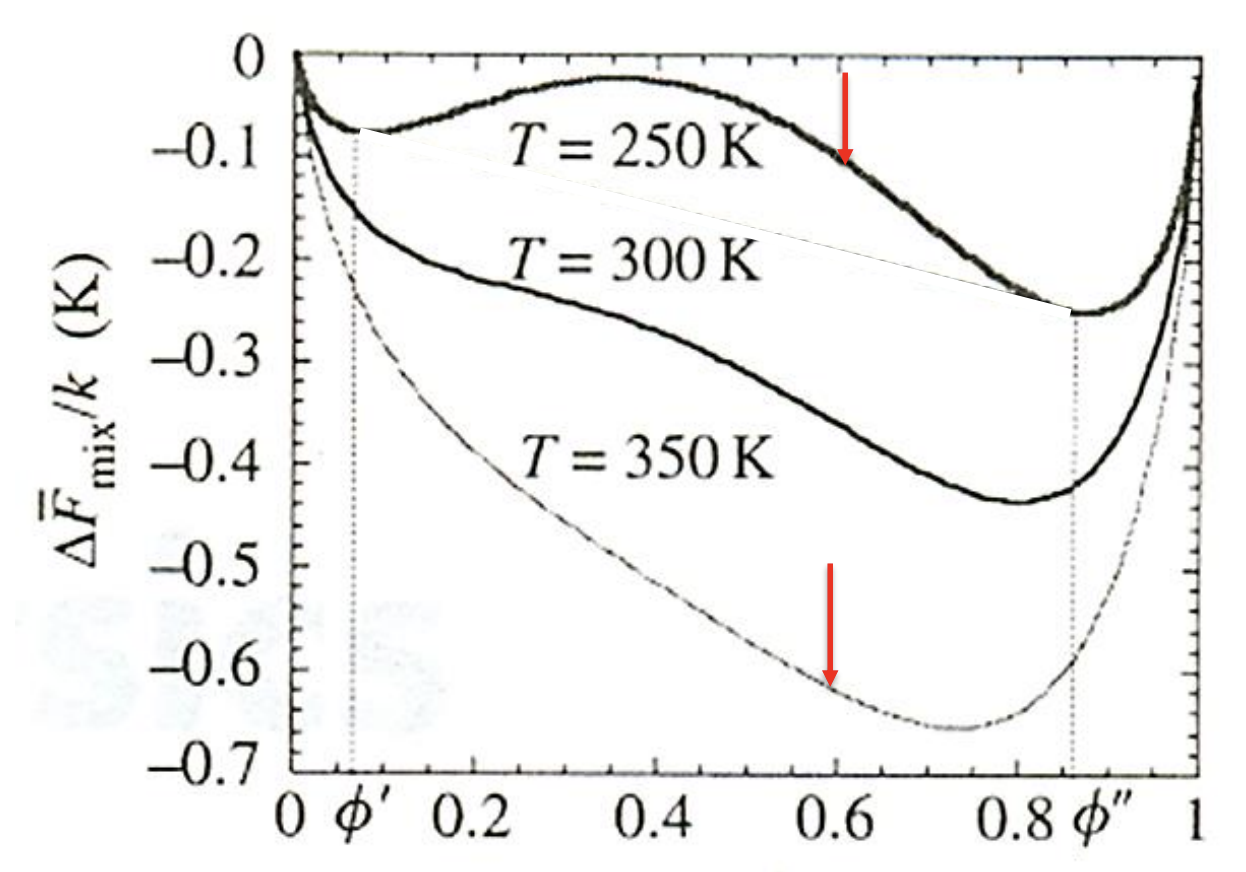
energy curve로 또 알 수 있는 점은 어떤 조성, $\phi$값에서 phase seperation이 일어나는 지 mixing이 일어나는 지 알 수 있다. 이 때 $\alpha, \beta$상이 존재하게 되는 지점을 $\phi^{\prime}, \phi^{\prime\prime}$이라 하자. 두 지점을 이은 직선의 방정식보다 곡선이 아래에 위치하는 $\phi$ 값에서 mixing이 일어나고, 직선보다 곡선이 위에 위치하는 $\phi$값에서 phase seperation이 일어난다.

Phase seperation

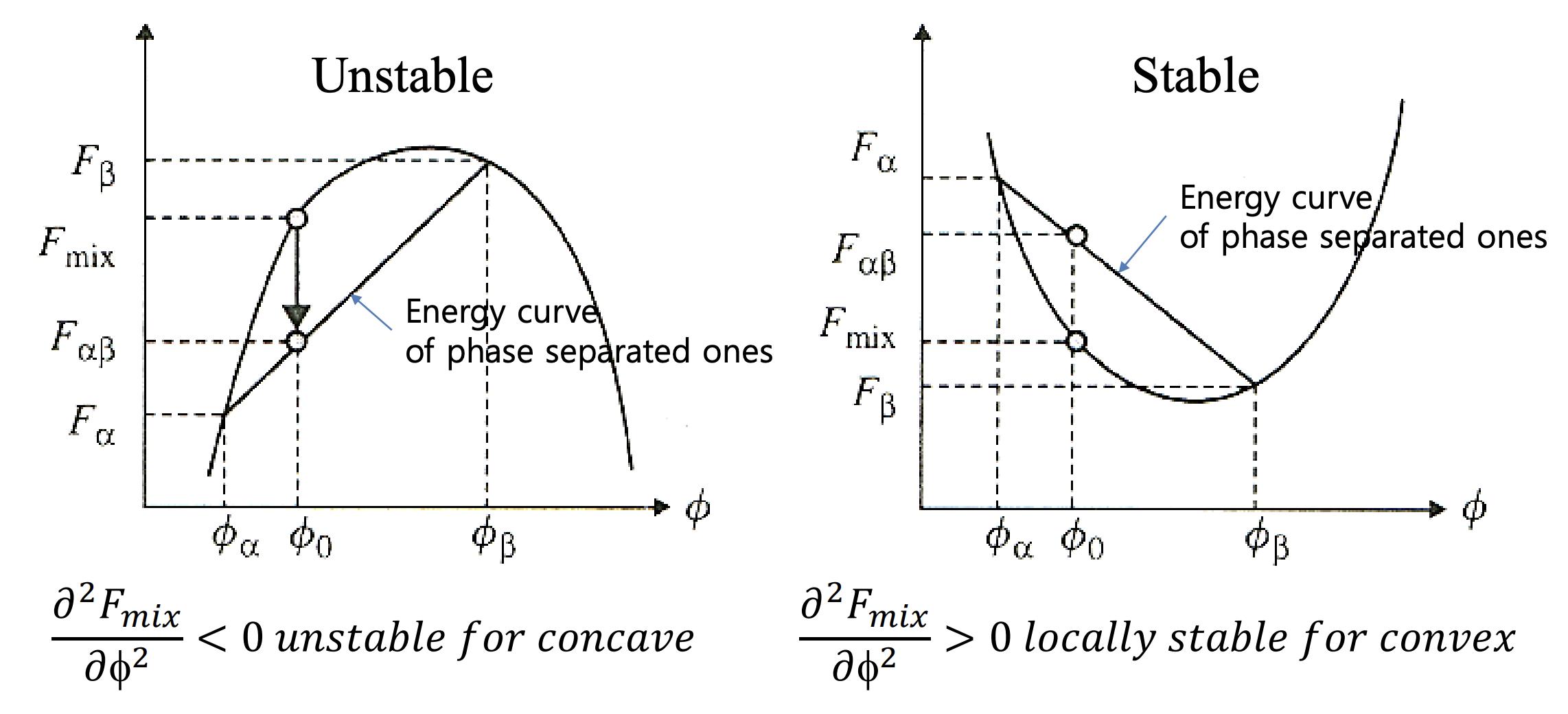
앞에서 설명했듯, $\alpha, \beta$ phase가 나타나는 조성을 $\phi_{\alpha}, \phi_{\beta}$라 하고 두 지점을 이은 직선보다 energy curve가 위에 있게 되는 $\phi_0$에서, mixing이 일어난다. 즉, $\frac{\partial^2 F_{mix}}{\partial \phi^2}$이 0보다 작은 경우, 위로 볼록한 곡선의 형태가 되고, 이는 불안정한 상태(unstable)임을 가리킨다. 반면 0보다 큰 경우, 아래로 볼록한 곡선의 형태가 되고, 이는 해당 구간에서 국소적으로 안정한(locally stable) 상태가 된다.

$f_{\alpha}$

고분자 혼합 용액에서 임의의 조성을 나타내기 위해, $\phi_0$라는 기호를 이용해서 표현하자. 이때 $\phi_{\alpha}, \phi_{\beta}$를 사용해서 나타내면 다음과 같다.

여기서 $f_{\alpha}, f_{\beta}$는 다음과 같은 관계를 따른다.

그럼 상 분리가 일어날 때의 에너지를 나타내는 직선의 방정식은 다음과 같다.

Ideal Cases

혼합용액의 $\Delta G^M, \Delta H^M, \Delta S^M$을 이전 시간에 배웠다. 이를 이용하여 entropic effect만 고려한 경우와 enthalphic effect만 고려한 이상적인 경우에서 energy curve가 어떻게 표현되고, 언제 phase seperation이 일어나는 지 알아보자.

Only Entropic

ideal case에서

여기서 only entropic effect만 고려하게 되면, enthalpy term의 값은 0이므로, 다음과 같다.

앞에서 혼합물의 에너지를 나타내는 함수를 두 번 미분한 이계도 함수가 음인지 양인지를 통해 unstable / locally stable 한 지를 알 수 있고, mixing이 되는지 seperation이 일어나는지를 확인할 수 있었다.

이계도함수의 값이 0보다 큰 양수이므로, 아래로 볼록인 함수가 된다. phase seperation이 일어나게 되는 지점을 이은 직선보다 아래에 위치하므로, 이는 mixing이 일어난다고 볼 수 있다. 즉, entrpic effect는 항상 mixing을 유발한다.

Only Enthalpic

ideal case한 혼합용액의 깁스 에너지 변화량을 나타낸 함수에서 only enthalpic effect만을 고려하면 다음과 같다.

그러므로 $\phi_1$에 대해 두번 미분한 이계도 함수는 다음과 같다.

즉, $\chi$를 나타내는 상수 중 $B$의 부호에 따라 달라진다. 만약 $B$의 값이 음수라면, 이계도미분의 값이 양수이므로 mixing이 일어나게 되고, $B$의 값이 양수라면, 이계도미분의 값이 음수이므로 phase seperation이 일어난다.

Real Mixtrue

이제 ideal한 case가 아닌 entropy와 enthalpy term을 모두 고려한 real mixture의 energy curve를 살펴보자.

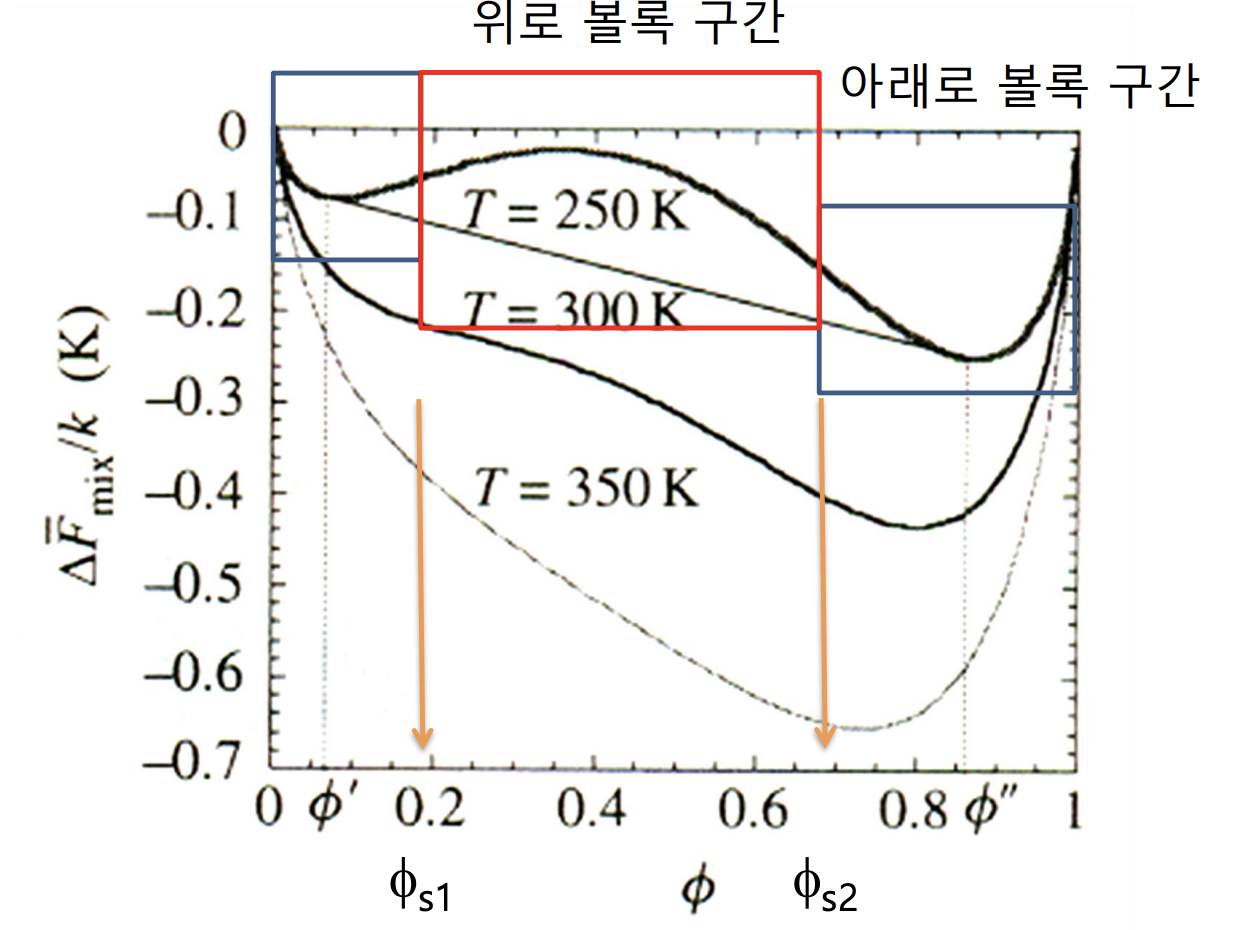
entropic effect와 enthalphic effect를 모두 고려했기에 위로 볼록한 구간과 아래로 불록한 구간이 모두 나타나는 것을 볼 수 있다. 앞에서도 이야기했지만, 온도가 증가함에 따라 전체적인 energy curve의 값이 낮아지게 되고, 점차 위로 볼록한 부분이 사라지는 경향을 보이는데 그 이유를 알아보자. 또한 real mixture의 energy curve에 영향을 주는 다른 요인인 조성(composition)도 알아보자.

Temperature Effects

real mixture의 $\Delta \bar{G}^M$은 다음과 같다.

이것을 두번 미분하게 되면,

우선 일반적으로 온도가 증가하게 되면, 혼합 용액의 entropy는 증가하게 될 것이다. 온도가 증가하면 분자 운동이 더 커지고 이에 따른 무질서도가 증가하기 때문이다. 그렇다면 온도가 높은 상태에서, entropy term에 의한 값이 enthalpy에 의한 값보다 더 커지게 되고 이는 entropic effect가 지배적(dominant)이라는 말이 된다. only entropic effect는 앞에서 봤듯, 항상 mixing을 유발하기에 전체적으로 energy curve가 아래로 볼록인 경향을 띠게 된다.

반면 온도가 낮은 경우에서는 위와 반대의 경향을 띄게 되어 entropy term의 값이 작아지고, enthalpy term의 값이 지배적(dominant)이게 된다. 그러므로, 온도가 낮아질수록 energy curve는 위로 볼록인 그래프가 눈에 띄게 나타난다. 위로 볼록인 부분에서 phase seperation이 관찰되는데, 특정 온도($T_c$)보다 낮아지는 경우에 phase seperation이 관찰되는 위로 볼록인 energy curve가 그려진다. 해당 온도 값인 $T_c$를 critical temeprature라고 한다.

Composition Effects

$\alpha, \beta$ phase가 관찰되는 조성을 $\phi_{\alpha}, \phi_{\beta}$이라 하자. 그리고 $\Delta \bar{G}^M$을 이계도 미분했을 때, 그 값이 0이 되게하는 변곡점의 조성을 $\phi_{s1}, \phi_{s2}$이라 하자. 그럼 다음과 같이 energy curve에서 경우를 나눌 수 있을 것이다.

Case 1 : Homogeneous mixed state

위 범위 내에 조성에서 혼합용액은 homogeneous mixed state가 된다. 즉, 균일하게 혼합된 상태로 특정 성분의 조성이 낮기에 에너지적으로 안정한 상태가 된다.

Case 2 : Unstable phase separation

위 범위 내에 조성에서 energy curve의 이계도미분한 값은 0보다 작아져 위로 볼록한 상태가 된다. 이는 unstable한 상태가 되고, 상의 분리(phase separation)이 일어나게 한다. 상의 분리가 일어나는 일반적인 형태를 spinodal decompositon이라 하는데, 위 구간의 unstable한 영역에서 관찰된다. spinodal decomposition은 핵 형성(nucleation)없이 자발적(spontaneous)으로 상의 분리가 일어나는 현상으로 한 종의 농도가 많고, 다른 종의 농도는 낮아지는 두 가지 공존 상으로 분리될 때 관찰된다. 두 상이 거의 동일한 비율로 나타나면 특징적인 얽힌 구조가 형성되고 점차 분리된다.

Case 3 : Metastable phase separation

위 범위에서도 energy curve는 phase seperation 직선보다 위에 위치하기에 phase separation이 일어나게 된다. 다만, case 2와 차이가 있는 것은 case 2보다는 비교적 안정한 상태로 자발적으로 상의 분리가 관찰되지는 않는다. 이때 상의 분리가 일어나기 위해서는 큰 fluctuation(응집/응집체)가 있어야 한다. 즉 nucleation and growth 메커니즘에 의해 상의 분리가 일어나게 된다.

Symmetric blend and Assymetric blend

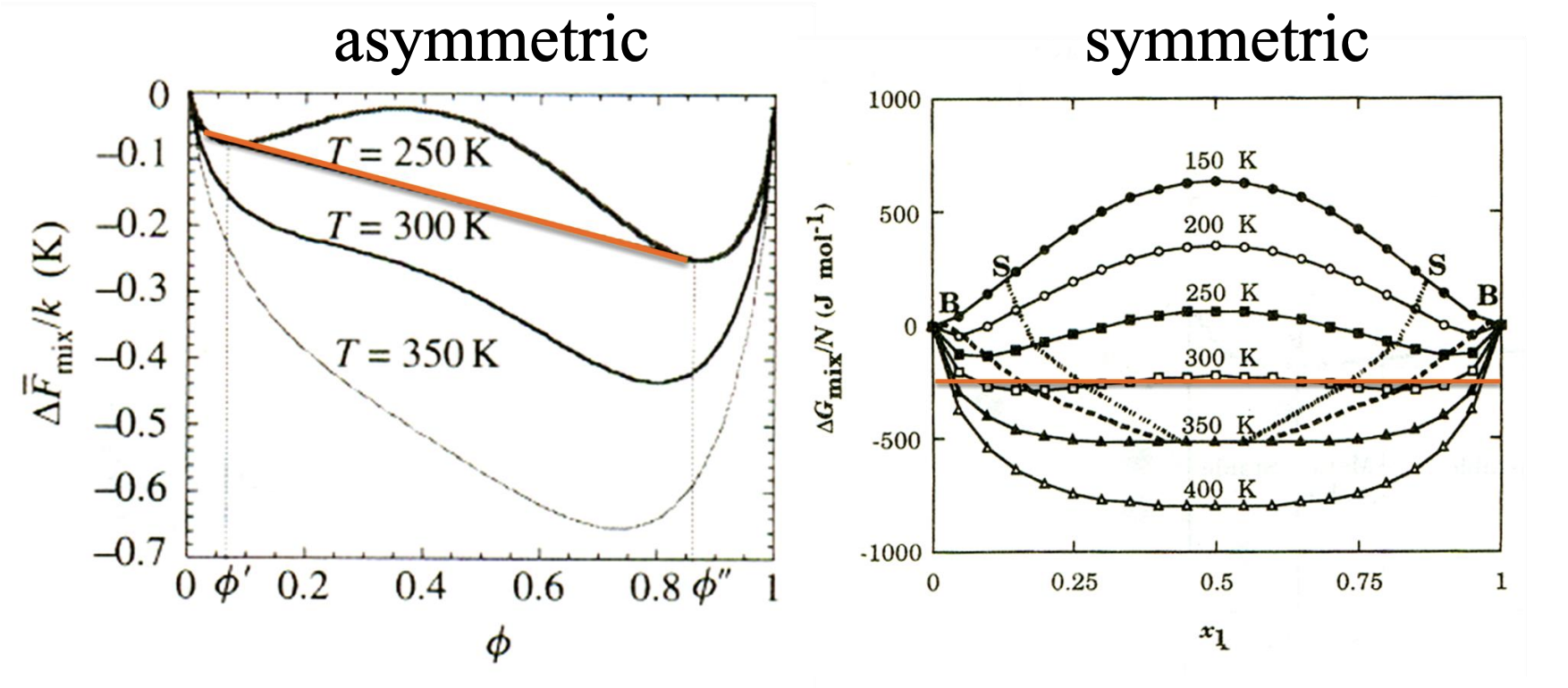
symmetric blend는 두 고분자의 성분, 크기나 화학적 구조가 비슷한 경우를 의미한다. 두 고분자의 크기가 비슷해지면 분자량과 체적 분율이 대칭적이 되고, 혼합물의 자유 에너지도 대칭성을 띄게 된다. 그러므로 상의 분리가 일어날 때 그 형태가 대칭적이 될 가능성이 높다.

assymetric blend는 두 고분자 성분이 크기(분자량)나 화학적 구조에서 상당한 차이를 가지는 경우를 말한다.

Phase Diagram

이제 energy curve를 통해 phase separation이 일어나는 영역과 mixing이 일어나는 영역, phase separation이 일어나는 영역 중 어느 지점에서 spinodal decomposition이 일어나는 지와 nucleation and growth가 일어나는 지 알 수 있었다. 이번엔 위에서 설명한 symmetric blend와 assymetric blend의 energy curve를 통해 물질의 상(phase)이 온도, 압력, 조성 등의 변수에 따라 어떻게 변하는지를 나타내는 phase diagram을 구해보자.

우선 polymer blend의 phase diagram을 조성에 따른 온도의 변화에 따라 상이 어떻게 관찰되는지를 알아본다고 하자. 그러면 중요해지는 지점은 2개이다. 바로 혼합물의 깁스 자유 에너지를 한 번 미분했을 때 0이 되는 지점과 이계도미분 값이 0이 되는 지점이다. 이 두 지점을 통해 stable / unstable / metastable을 구분할 수 있으며, 이에 따라 상의 변화를 판단할 수 있다. 한 번 미분했을 때 0이 되는 지점을 binodal point라고 하고, 두번 미분했을 때 0이 되는 지점을 spinodal point라고 한다.

Phase diagram of symmetric blend

우선 symmetric blend의 경우, 위에서 정의한 mixture의 깁스 자유 에너지 변화량, $\Delta \bar{G}^M$에서 상수 $r_1, r_2$의 값이 같다. 그러므로 다음과 같이 표현할 수 있다.

그럼 $\Delta \bar{G}^M$은 다음과 같다.

그럼 binodal point는 다음과 같다.

그리고 spinodal point는 다음과 같다.

위 과정은 energy curve를 통해 $x$축을 $\phi_1$(조성, composition)에 대해 $y$축을 $r \chi$로 나타내 phase diagram을 plot할 수 있다. 그 결과는 다음과 같다.

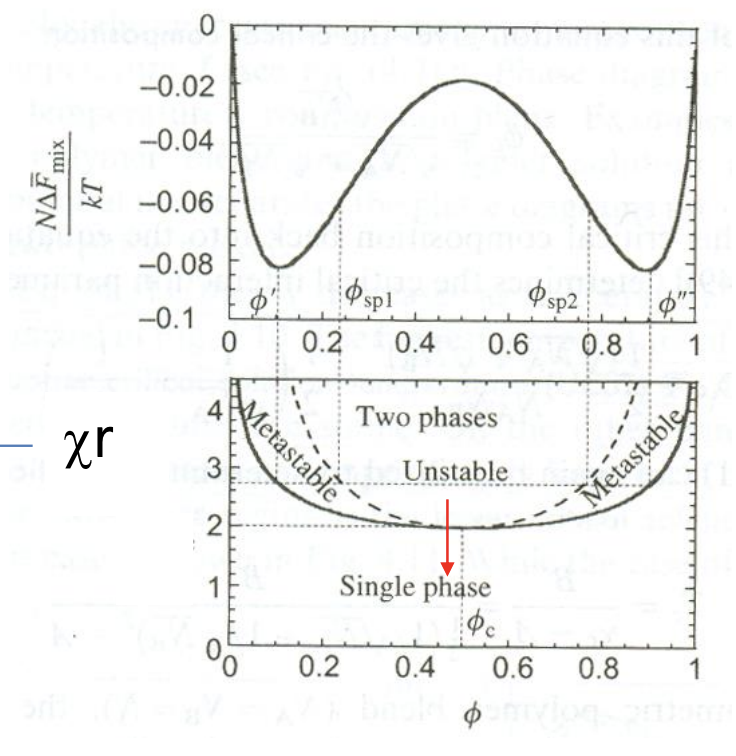
위 그래프에서 실선이 binodal point, 점선이 spinodal point를 의미한다. 점선보다 안쪽에 위치하는 조건($\phi, r, \chi$)에서 two phase로 phase seperation이 일어날 것이다. 반면 실선보다 바깥쪽에 위치하는 조건에서는 symmetric blend가 one phase로 나타나고 이는 mixing이 일어남을 의미한다.

여기서 $y$축에 해당하는 변수 $r\chi$를 온도 $T$에 대해 나타낸다고 하면, $\chi$를 다음과 같은 형태로 나타낼 수 있음을 기억하자.

UCST

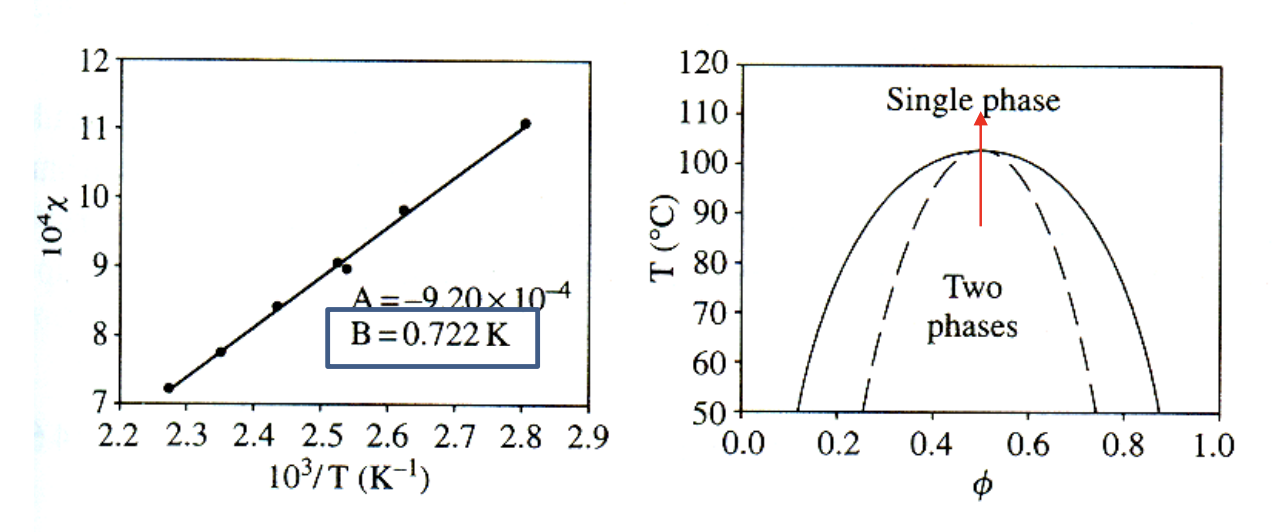
앞에서 $\chi$는 enthalphic effect를 반영한다고 배웠다. $\chi$를 나타내는 상수 중 $B$값에 따라 mixing을 유발하는지 phase separation을 유발하는지 알 수 있었다. UCST는 Upper Critical Solution Temeperature라는 뜻으로, 위 그래프 중 좌측의 plot과 같이 $\chi$의 값이 온도가 상승함에 따라 감소하는 경향을 띄게 된다. ($x$축의 값이 $T^{-1}$임에 유의하자.) 즉, $B > 0$인 경우를 의미한다. 그러므로 phase diagram은 우측의 plot과 같이 위로 볼록인 형태를 띄게 되고 온도가 상승하면 two phase(phase separation)에서 one phase(mixing)의 경향을 보인다. 즉, 온도가 올라가면 mixing이 일어나는 일반적인 경우를 의미한다.

LCST

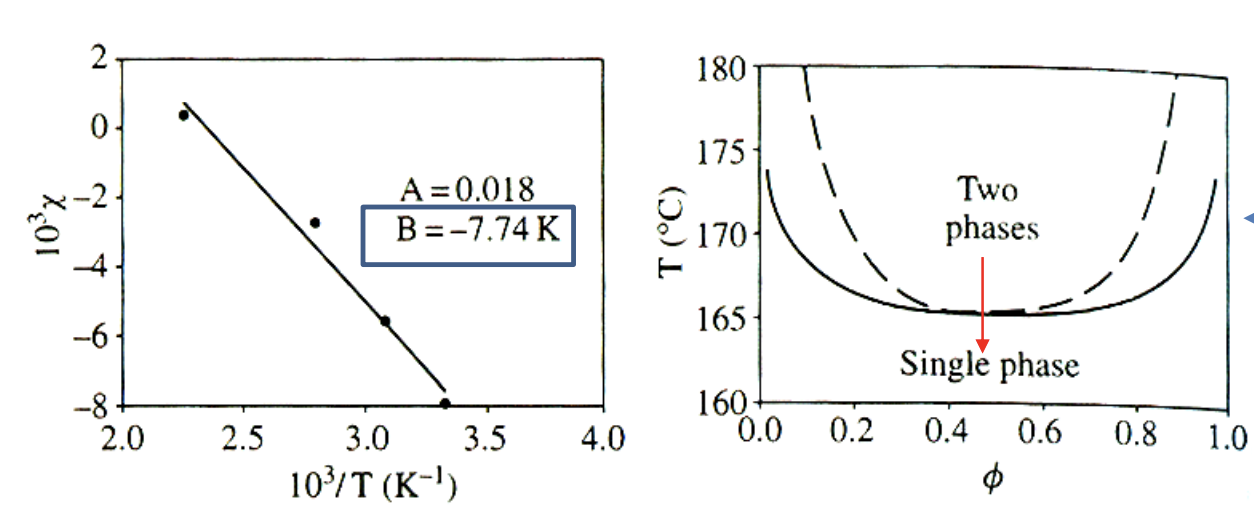
$B < 0$인 경우, 온도가 증가함에 따라 $\chi$값이 증가하는 경향을 보인다. 이때를 LCST라고 하며, Lower Critical Solution Temperature를 의미한다. phase diagram은 우측의 plot과 같이 나타난다. UCST와 반대로 온도가 상승하면 one phase(mixing)에서 two phase(phase separation)로 변하는 경향을 보인다. 즉, 온도가 올라가면 separation이 일어나는 특이한 경우이다.

Molecular Weight Dependence

symmetric blend가 되는 고분자 blend를 생각해보자. 이 때 binodal point와 spinodal point가 되는 $r\chi$값은 각각 다음과 같다.

이렇게 구한 $r\chi_s$의 분자량(molecular weight)에 대한 의존성을 알아보자. symmetric blend의 spinodal point 그래프를 조성 $\phi_1$에 대해 편미분하여 0이 되는 critical point를 구해보면 다음과 같다.

그러므로 symmetric blend의 phase diagram 중 spinodal point의 critical point의 $x$좌표 $\phi_c$는 항상 $0.5$가 됨을 알 수 있다. 이때 spinodal point의 값($y$값)은

이 된다. 여기서 $N$은 molecular weight에 비례하는 값으로, 분자량이 증가할수록($N$이 증가할수록) two phase와 one phase를 구분짓는 변곡점, critical point의 $x$값 $\phi_c$는 $0.5$로 고정이지만, $y$값에 해당하는 $\chi_c$는 점차 감소하는 것을 확인할 수 있다. 또한, 분자량이 증가할수록 $\chi_c$가 감소한다는 의미는 two phase 영역이 넓어진다는 것으로 해석할 수 있다.

Phase diagram of assymetric blend

assymetric blend를 나타내는 예시는 polymer solution이 있을 것이다. polymer solution의 경우에는 $r_1 = 1$인 경우로 볼 수 있다. 그럼 $\Delta \bar{G}^M$은 다음과 같이 나타난다.

위 함수를 $\phi_2$에 대해 한 번 미분하여 0이 되는 binodal point를 찾으려고 시도하면, 존재하지 않는다. 즉, 오직 spinodal point만 구할 수 있으며, "assymetric blend의 phase diagram은 spinodal point만 나타난다"를 의미한다. 구한 spinodal point를 $\chi_s$라고 하면 다음과 같다.

우리는 앞에서 symmetric blend의 molecular weight에 대한 의존성을 확인하기 위해 $\chi_s$의 critical point를 찾고, molecular weight를 의미하는 $N$에 대한 의존성을 확인했었다. 동일한 과정을 assymetric blend에 적용해보자.

Critical Point

분자량에 대한 의존성을 확인하기 위해 $\chi_s$의 critical point를 찾아보자. $\chi_s$를 $\phi_2$에 대해 편미분하여 0이 되는 지점을 찾자.

위 등식을 성립하게 하는 $\phi_2$의 값을 $\phi_c$라고 하면, 다음과 같다.

이렇게 구한 $\phi_c$를 $\chi_s$에 대입한 결과를 $\chi_{s,c}$라고 하자. 그 결과는 다음과 같다.

그럼 최종적으로 구한 assymetric blend(polymer solution)의 spinoddal point, $\chi_s$에 대한 critical point는 다음과 같다.

Molecular Weight Dependence

이제 분자량에 대한 의존성을 알아보자. 앞에서 $r \approx N$이라는 근사를 사용했듯이 동일하게 적용하고, 분자량을 증가시키면($N \rightarrow \infin$), $\phi_c \rightarrow 0$에 수렴하고, $\chi_{s,c} \rightarrow 0.5$에 수렴한다는 것을 알 수 있다. 즉 분자량이 증가할수록 상의 분리가 일어나는 two phase region이 넓어지는 것을 확인할 수 있다. 그런데 우리는 앞에서 $\chi = A + \frac{B}{T}$를 나타내는 관계식에서 $B$의 부호에 따라 UCST인지 LCST인지 구분했었다. 하지만 다행히도 두 경우(UCST, LCST) 모두 분자량이 증가할수록 $\chi_c$는 감소하는 경향을 띄고, two phase region이 넓어진다.

Polymer blends

위에서는 $r_1 = 1$인 polymer solution인 경우를 symmetric blend로 가정했고, $r_1 = r_2 = 1$인 이상적인 polymer blend를 assymetric blend로 가정하고 phase diagram을 그려보았다. 또한 phase diagram의 spinodal point를 통해 critical point가 어떻게 변하고 분자량에 따라 어떤 경향을 띄는지도 확인했다. 하지만 이번엔 좀 더 일반적인 경우(general case)를 생각해보자. 즉, $r_1 \neq r_2$를 가정해보자.

위 식을 $\phi_2$에 대해 두번 편미분하여 얻게되는 $\chi_s$는 다음과 같다.

Critical Point

이제 spinodal point, $\chi_s$의 critical point를 찾아보자.

이를 계산하여 구한 $\phi_{2,c}$는 다음과 같다 ($1-\phi_1 = \phi_2$임을 기억하자.)

이 값을 대입하여 $\chi_{s,c}$를 구해보면 다음과 같다.

그러므로 critical point는 다음과 같다.

위 식이 general case인 polymer blend의 critical point인 이유는 당연히 $r_1 = r_2$로 두게 되면 위에서 상정한 symmetric blend로 symmetric blend의 criticl point인 $\left(\frac{1}{2},\; 0 \right)$이 된다. 반면, $r_1 = 1$을 대입하면 polymer solution, assymetric blend가 되고 critical point는 $\left(0,\; \frac{1}{2} \right)$이 된다. 물론 두 critical point는 매우 긴 chain(분자량이 큰)을 갖는 $r \rightarrow \infin$을 가정한 것이다.

Fractionation

고분자를 중합하게 되면 분자량이 큰 놈도 있을 것이고 작은 놈도 존재하게 된다. 이를 분리하기 위해 chromatography를 사용하기도 하지만 비용상의 문제로 fractionation을 사용하기도 한다. fractionation은 분자량의 차이를 이용하여 분리하는 방법이다. polymer solution에서 non-sovlent를 넣게 되면 $\chi$의 값이 점점 증가하게 된다. $\chi$값이 증가한다는 의미는 one phase에서 two phase로 상의 분리가 일어난다는 것을 의미한다. 우선 분자량에 따른 phase diagram은 고정적이다. high molecular일수록 phase diagram의 critical point가 $(0, \frac{1}{2})$에 가까워진다. non-sovlent를 넣게되면 $\chi$값이 증가하기 때문에 high MW의 고분자는 two phase 영역으로 이동하게 되어 상의 분리가 일어나지만, 상대적으로 low MW의 고분자는 여전히 one phase에 존재한다. 즉, non-solvent를 계속해서 첨가해주면 LCST, UCST 두 경우 모두에서 높은 분자량에서 낮은 분자량의 순서로 석출할 수 있게 된다.

또 다른 fractionation의 방법으로는 $T$, 온도의 조절이다. UCST의 경우 높은 온도에서 낮은 온도로 온도를 낮춰주게 된다. 처음에는 high MW, low MW의 고분자 모두 one phase 상에 존재하겠지만, 온도를 낮춰주면 high MW부터 먼저 two phase상으로 이동하여 상의 분리가 일어난다. LCST의 경우, 그려지는 phase diagram은 다르지만(위로 볼록에서 아래로 볼록) 온도를 높여주면 동일하게 높은 분자량의 고분자에서 낮은 고분자의 순서대로 석출(상의 분리)된다.