[고분자 물리] Viscoelastic Properties

jmt·2024년 6월 13일

고분자물리

목록 보기

12/13

Introduction

Rheology는 유변학으로 흐름과 변형을 연구하는 학문이다. 물체에 가해진 힘이 흐름과 변형으로 나타나는데, 이때 물체마다 나타나는 성질이 다르다. 흐를 수 있는 유체를 생각해보자. 유체에 어떠한 힘을 가하면 흐름이 발생할 것이고, 꿀처럼 점성이 있는 유체는 비가역적인 변형(irreversible deformation)이 될 것이다. 욕조에 꿀을 채우고 손을 휘저어 흐름을 발생시켰을 때, 우리는 손을 휘젓기 전으로 상태를 돌릴 수 없으니까 점성이 있는 유체는 비가역적인 변형이 일어난다. 고체의 경우에도 딱딱한 물체의 경우에는 일정 이상의 힘을 가하면 파괴가 일어나겠지만 고무처럼 탄성이 있는 경우에는 힘을 가하면 그 전 상태로 돌아오게 된다. 에너지가 저장되는 성질이 나타나는 것이다. 그런데 고분자 물질에서는 점성과 탄성의 성질이 모두 나타나는 것처럼 보이는 점탄성(viscoelasticity)를 띈다. 나중에 설명하겠지만 점탄성은 시간에 의존적인(time dependent)한 성질이다.

Strain and Stress

strain은 변형률을 stress는 응력을 이야기한다. 변형률(strain)은 단어 뜻 그대로 얼마나 변형이 일어났는지를 설명하는 값이다. 응력(stress)의 경우에는 비교적 낯선 단어지만 압력이라고 생각하면 간단하다. 즉, 단위 면적당 가해지는 힘을 이야기한다. 물체의 변형(deformation)을 이야기할 때 어떤 물체에 어떤 힘을 가하냐에 따라 여러 mode로 strain / stress를 정의할 수 있는데 대표적으로 elongation mode와 shear mode가 있다.

Elongation Mode

elongation mode의 elongation은 연신율, 신율로 번역된다. 시료가 얼마나 늘어나는 지를 나타내는 지표가 연신률이다. 즉, 어떤 물체를 늘리는 변형을 가했을 때를 의미한다. 이때의 strain과 stress는 각각 다음과 같이 정의한다.

\text{strain : }\varepsilon = \frac{dx}{x_0};\quad \text{stess : }\sigma = \frac{F}{A}.

응력(stress)은 단위 면적 당 힘이라 하였으니 기존의 물리량을 나타내는 기호로 표현했다. 변형률(strain)의 경우에 $dx$ 는 변화한 정도이다. $x_0$ 으로 normalize하는 이유는 간단하다. 어떤 재료에 힘을 가하여 일어나는 변형의 정도는 그 자체로 아무 의미 없는 값이 된다. 예를 들어 전체 길이가 10cm에 도달하는 재료에 힘을 가하여 1cm 변화한 것과 1000cm의 재료에 힘을 가하여 1cm 변화한 것이 같지 않기 때문이다. 그렇기에 힘을 가하기 전, 변형이 일어나기 전 재료의 dimension,(여기서는 길이)을 나타내는 값 $x_0$ 를 사용하여 normalize한다.

Shear Mode

shear mode에서 shear는 전단으로 번역된다. 즉, 다음 그림과 같은 경우에 가장 윗 층에 어떠한 힘을 가하였을 때를 의미한다.

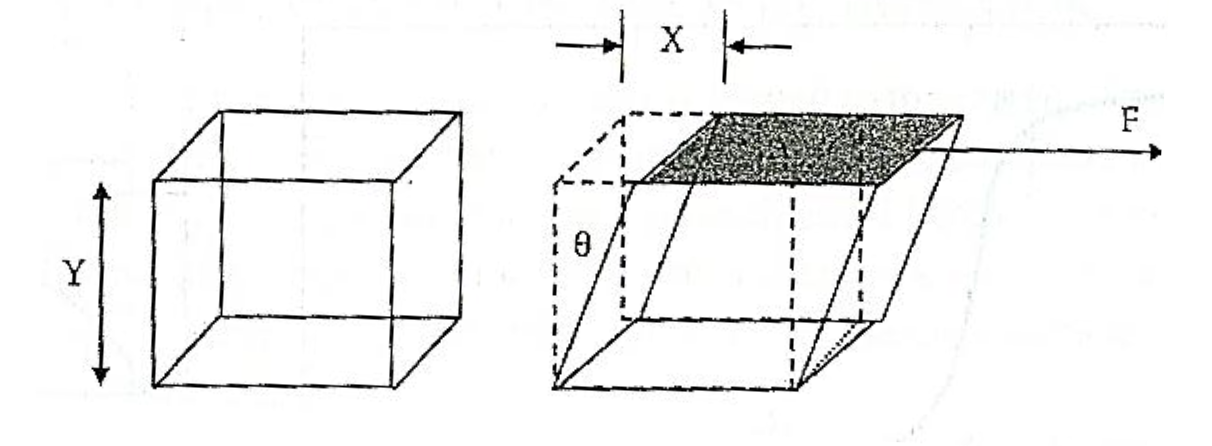
이때 shear과 stress는 각각 다음과 같이 정의한다.

\text{strain : }\varepsilon = \frac{x}{y};\quad \text{stess : }\sigma = \frac{F}{A}.

Constitutive Equation

구성 방정식(constitutive equation) 물리학이나 공학 등에서 '변형 가능한 물체에 외부 힘이 작용하였을 때 발생된 내부 저항력과 변형도 간의 관계식'을 말한다.
(From Wikipedia)

그 중 고체(solid) 중에서도 이상적인 탄성체(ideal elastic)의 경우에는 다음과 후크의 법칙(Hook's Law)라는 구성 방정식을 따른다.

\tau = G \gamma

$\tau$ 는 stress, $\gamma$ 가 strain이 되고, $G$ 의 경우 비례상수로 modulus라고 한다. 즉, stress와 strain이 linear한 관계가 되는 것이다. elongation mode에서는 $\sigma = G \varepsilon$ 으로 표현하게 된다.

액체의 경우에는 뉴턴 유체(newtonian fluid)는 다음과 같은 구성 방정식을 따른다.

\tau = \eta \dot{\gamma}

여기서 $\dot{\gamma}$ 는 strain rate, 전단율로 변형률인 $\gamma$ 를 시간 $t$ 에 대해 미분한 값이다. 고전 역학에서 어떤 변수에 대한 미분(주로 시간)을 $\dot{\quad }$ 기호로 표현했었다. 그리고 여기서 비례 상수에 해당하는 $\eta$ 는 점도를 의미한다. 즉, 뉴턴 유체는 변형 속도와 stress가 linear한 비례 관계를 갖게 된다. 물론 주의점은 후크의 법칙과 뉴턴의 유체 법칙은 오직 아주 작은 변형률과 변형 속도(small strain or strain rate)에서만 유효하다.

Non-Newtonian

비뉴턴 유체는 어떤 거동을 보이고 구성 방정식은 어떻게 될까? 우선 다음 그림을 보자.

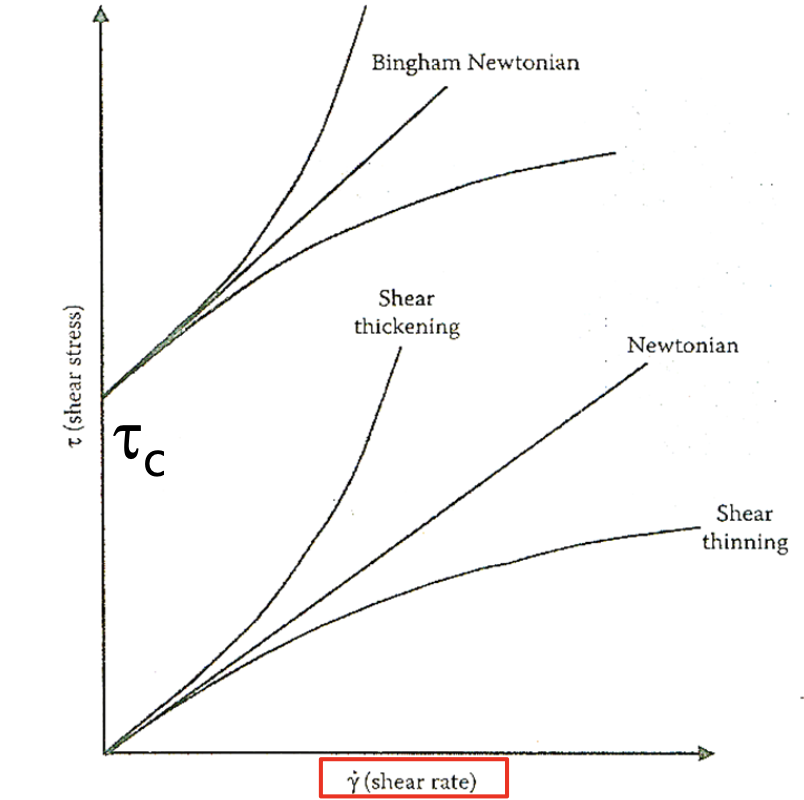
뉴턴 유체를 보면 shear rate와 stress간의 관계가 선형적이다. 이때의 기울기가 점도인 $\eta$ 가 된다. 이러한 선형 관계를 따르지 않는 유체들은 모두 비뉴턴 유체라고 할 수 있다. 위 그래프를 보면 shear thinning이 일어나는 유체는 shear rate가 증가함에 따라 점도가 줄어드는 경향을 보인다. 마요네즈를 생각해보면 된다. 빵에 마요네즈나 잼을 바를 때, 처음에는 점성이 매우 높아 잘 발리지 않지만, shear rate가 높아지면 점도가 낮아져 잘 발리게 된다. 또한 shear thickening은 shear rate가 높아짐에 따라 점도 $\eta$ 가 증가하는 경향을 보인다. 그리고 Bingham Fluids의 경우에는 일정 이상의 shear stress( $\tau$ )가 가해진 이후에 점성이 나타난다. 즉, 일정 이상의 힘을 가해야 변형이 일어나는 유체라 볼 수 있다. 그리고 이때의 shear stress를 critical shear stress( $\tau_c$ )라 한다.

Time-Dependent

점탄성은 time-dependent한 성질이라 하였는데 그 이유는 맨틀을 예시로 떠올려보자. 맨틀은 고체와 액체의 중간 상태라고 고등학교에서 배웠을 것이다. 중간 상태라고 부르는 이유는 관측 시간 때문이다. 맨틀의 변형 정도를 매우 짧거나 일반적인 시간인 1분 혹은 1시간 정도의 시간에서 관찰했을 때, 변형률을 계산할 수 있을까? 매우 정밀한 기계로 정밀한다면 아주아주 작은 값에서의 변형이 일어났을 수도 있지만(지각 변동에 의해) 일반적인 관측 기기로 측정한다고 하면, 변형률이 0에 수렴한다. 즉, 어떠한 힘이 작용해도 비가역적인 변형이 일어나는 유체의 성질보다는 에너지를 저장하는 고체의 성질이 나타난다. 하지만 만약 관측 시간을 100년 혹은 1000년 정도로 두고 관찰한다면 분명한 변형률과 변형 속도를 측정할 수 있을 것이다. 그렇다면 맨틀은 유체인 것일까? 이렇게 time scale에 따라 물체의 성질(property)가 달라지는 것을 time-dependent한 성질이라고 한다. 점탄성도 이런 time-dependent한 성질이다.

예를 들어, 공이 튀는 현상을 관찰한다고 하자. 이때 짧은 시간을 두고 관찰한다면, 바닥에 충돌한 뒤 다시 위로 튀어오르고 에너지가 0이 될 때까지(물론 에너지는 보존되겠지만) 운동하는 고체로 관찰될 것이다. 그렇기에 Hookean Solid의 성질이 나타나겠지만, 긴 시간을 두고 관찰한다면, 아래 그림의 c와 같이 Newtonain Liquid의 성질이 나타날 것이다.

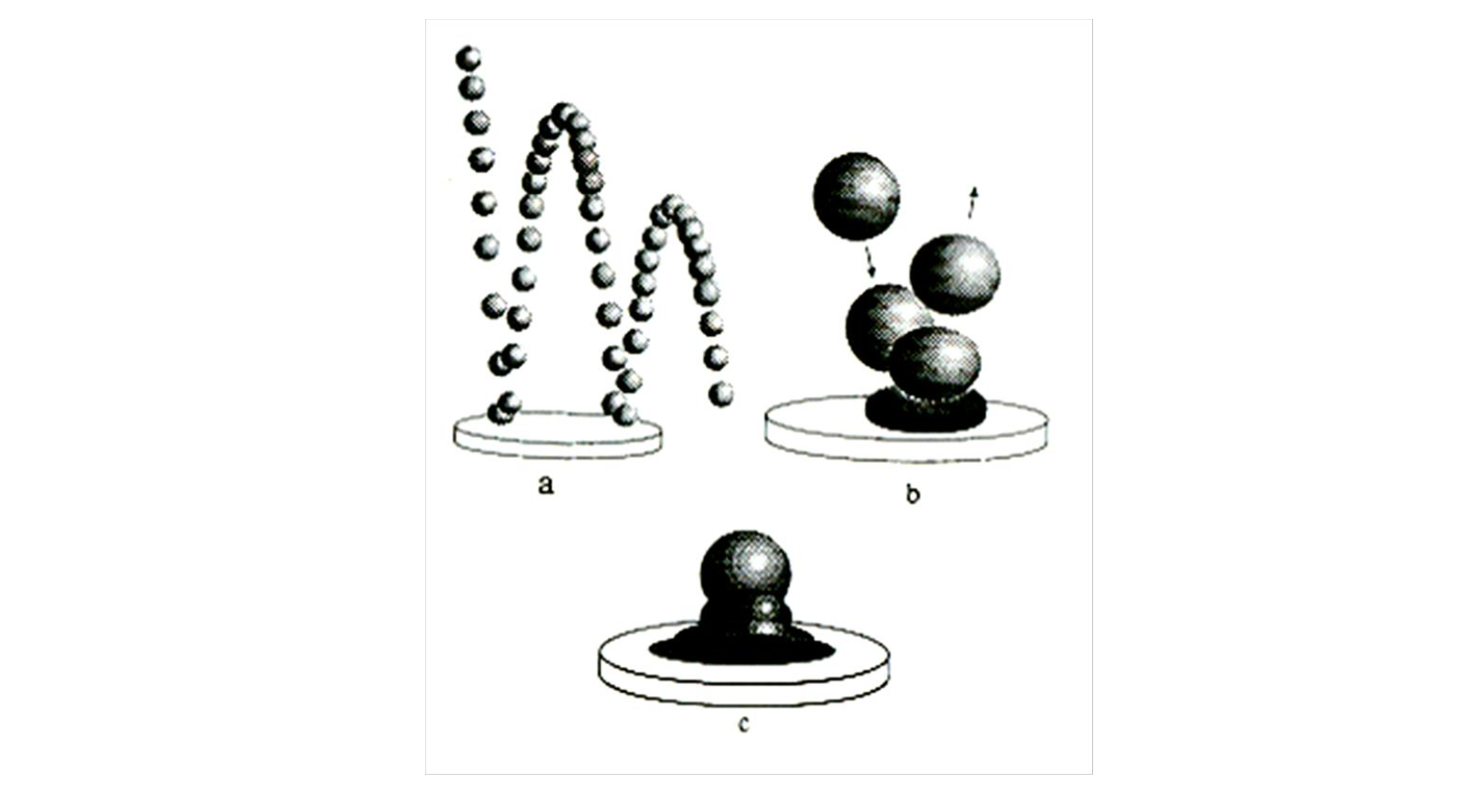
여기서 주의할 점은 짧은 시간과 긴 시간이 단순히 현상을 관찰하는 시간이라고 생각해서는 안된다. shear rate를 정의하는 $\frac{dr}{dt}$ 의 $t$ 를 의미한다. 그렇기에 짧은 시간(short time)에서는 비교적 높은 shear rate를 갖게 되고, 긴 시간(long time)에서는 비교적 낮은 shear rate가 된다는 것을 기억하자.

또한 시간( $t$ )와 점도( $\eta$ )의 관계에서도 time-dependent behavior가 관찰되는 유체가 존재한다. 여기서는 shear rate는 일정하다고 가정하고 시간에 대해 점도를 측정하여 아래와 같은 그래프를 얻었다.

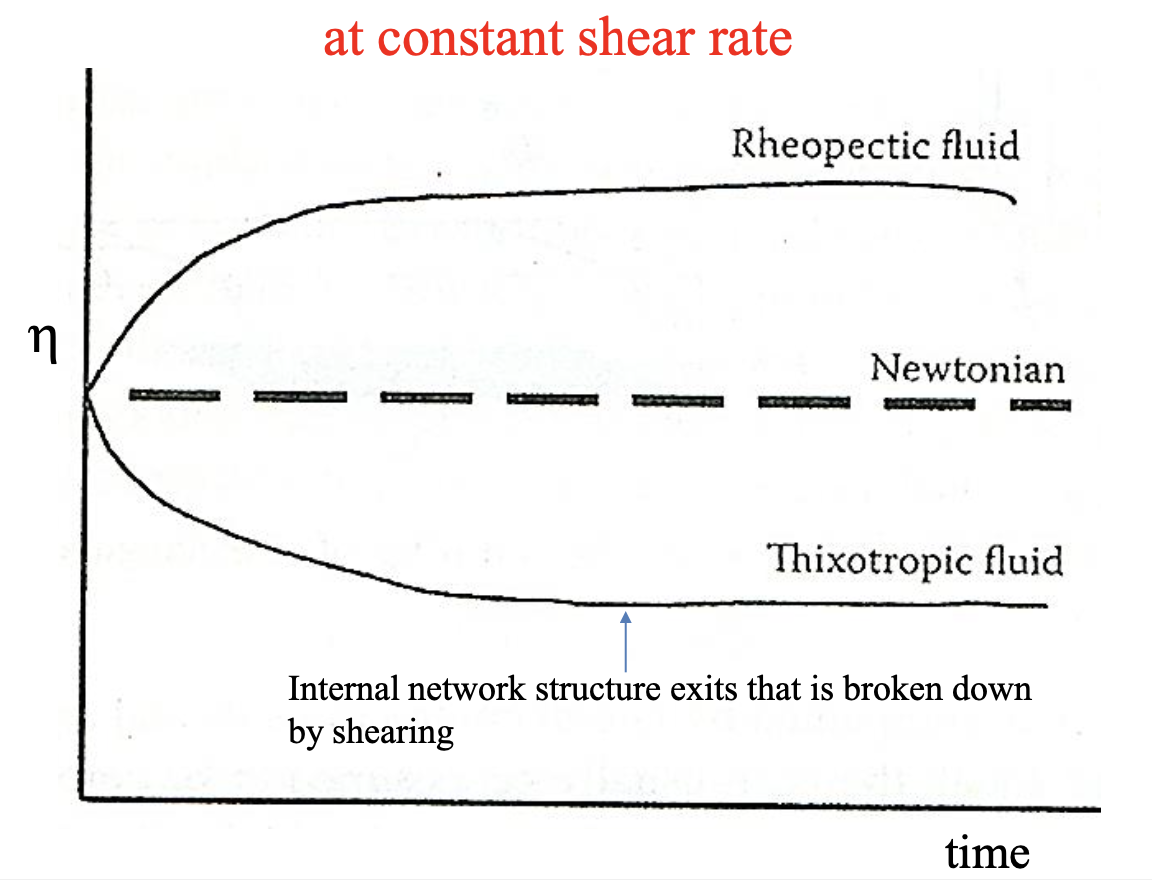
뉴턴 유체는 시간에 무관한 점도를 보이지만, Rheopectic fluid의 경우에는 시간이 지나면서 일정한 shear rate이지만, 점도가 증가하는 경향을 보인다. Thixotropic fluid의 경우에는 전단에 응력이 가해지며 내부 network 구조가 파괴되는 성질을 갖는다. 그렇기에 시간이 지나면서 점도가 낮아지는 경향을 보인다.

그렇다면 점탄성을 갖는 고분자 fluid에서는 어떠한 현상이 관찰될까?

Rod Climbing Effect

비커에 뉴턴 유체를 담고 중심에 막대를 넣어 회전하여 힘을 작용시키면, 유체에 흐름(flow)가 관측될 것이다. 하지만 점탄성을 띄는 고분자 fluid는 막대를 타고 올라가는 rod climbing effect가 나타난다. 이는 가해지는 shear force에 수직인 방향으로 normal force가 작용하여 나타나는 성질이다.

Ductless siphon

위 그림과 같이 배치하였을 때, 고분자 fluid는 관성처럼 변형을 유지하려고 한다. 그래서 관을 따라 유체가 올라가는 현상이 나타난다. 이는 고분자나 고분자처럼 복잡한 액체들은 전단(shear)보다 extension에 더 많은 점성이 작용하여 나타나는 현상이다.

Shear Viscosity

shear rate

힘과 전단율(shear rate)의 관계를 알아보기 위해 shear mode에서의 비례계수인 점도(viscosity)를 살펴보자. shear mode에서 stress는 기존과 동일하게 단위 면적 당 가해지는 힘으로 $\tau = F/A$ 가 된다. 변형률인 strain은 $X/Y$ 로 $tan\theta$ 값이 된다. 그리고 strain rate, 전단율은 다음과 같이 정의한다.

\dot{\gamma} = \frac{\dot{X}}{Y} = \frac{v}{h}

shear rate는 $X$ 축 방향의 변형 속도인 $dX/dt = \dot{X}$ 를 상판과 하판의 거리, gap인 $h$ 로 나누어준 값이다. 이 값을 속도 구배(velocity gradient)라고도 부른다.

Unit of Viscosity

뉴턴의 유체 법칙에 따라 $\eta = \tau / \dot{\gamma}$ 가 된다. stress는 우선 단위 면적 당 힘이기에 단위는 $N/m^2$ 이다. 그리고 위에서 정의한 shear rate에 따라 단위는 $1/\sec$ 이 된다. 그렇다면 점도 $\eta$ 의 단위는 다음과 같다.

\eta = \frac{\frac{N}{m^2} = \text{Pa}}{1/\sec} = \text{Pa} \cdot \sec

이를 SI unit으로 나타내면 다음과 같다.

\eta = \frac{\frac{kg \frac{m}{\sec^2}}{m^2}}{1/\sec} = \frac{kg}{m\cdot \sec}

그 외에 푸아즈(poise)라는 기호를 쓰기도 한다.

1 \text{poise} = \frac{1 \text{dyne}}{\text{cm}^2}\cdot \sec = \frac{10^{-5} N}{10^{-4} m^2}\cdot \sec = 10^{-1}\text{Pa}\cdot \sec

또한 물의 점도인 1 센티푸아즈( $1 \text{cP}$ )는 1 $\text{mPa} \cdot \sec$ 이다.

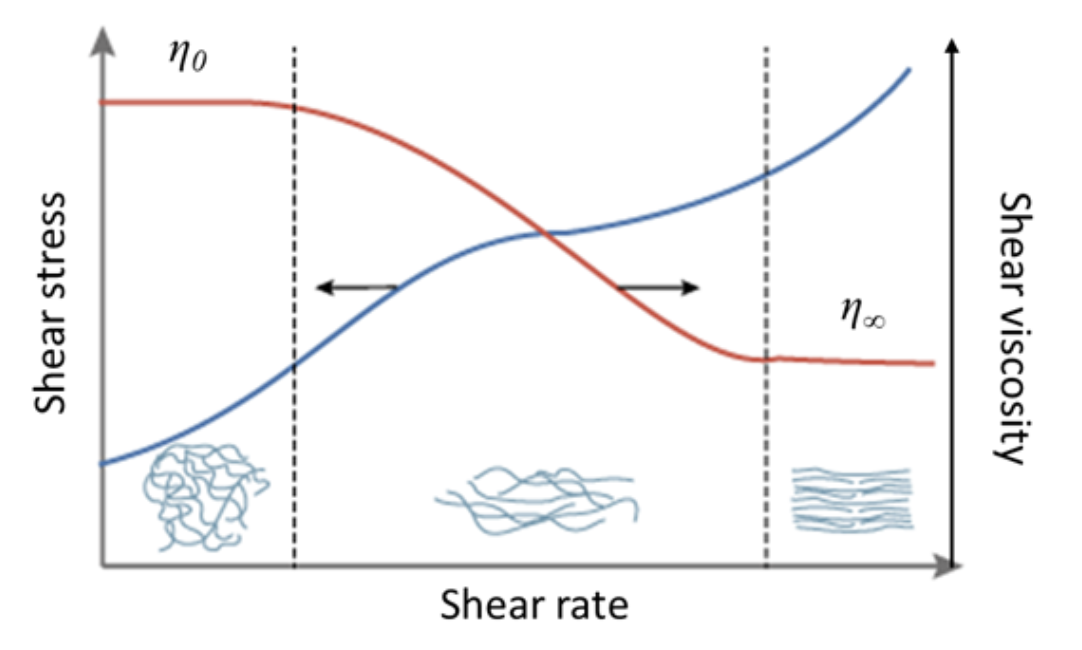
Four regions of visoelastic behavior

관찰이 가능한 time scale에서 점탄성 거동을 보이는 대표적인 물질이 polymer melt(or solution)이다. 그 중 polystyrene을 예로 아래와 같은 점탄성 거동을 확인할 수 있다. 이때 크게 4개의 영역으로 나눌 수 있다.

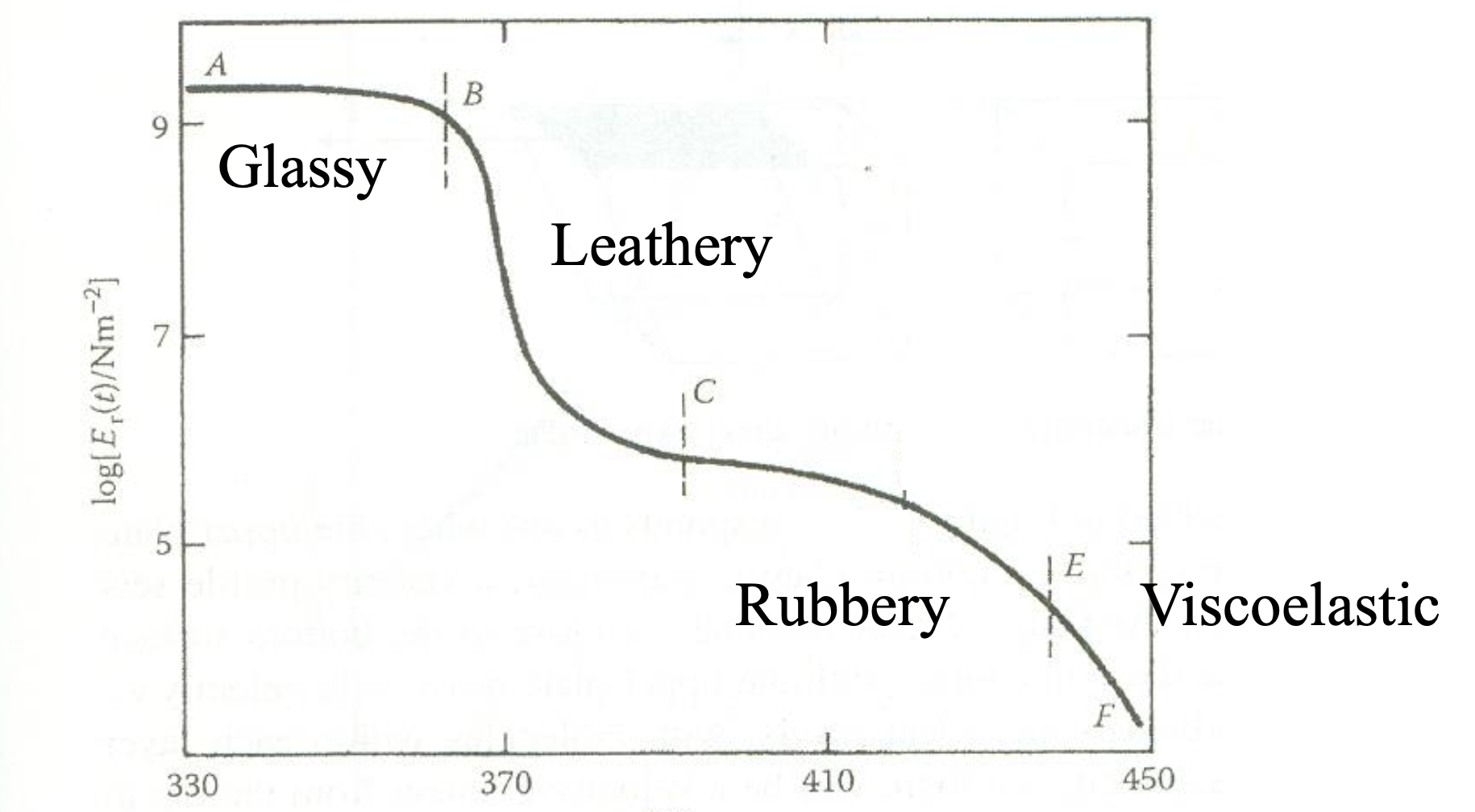
온도가 증가함에 따라 entanglement가 풀리는 flow region에서 점탄성 거동이 더 잘 관측된다.

Rheometer

rheometer는 위에서 이야기한 deformation / flow를 유발하는 장치이다. 이를 통해 strain이나 stress를 기기의 input으로 가할 수 잇게 된다. 그리고 output으로 stress이나 strain을 측정할 수 있고, 두 물리량 사이에 어떠한 관계가 있는지를 알 수 있게 해주는 측정 기기이다. 간단히 예를 들자면 shear mode는 다음과 같다.

\tau_{yz} = \eta \frac{dv_x}{dy} = \eta \dot{\gamma}

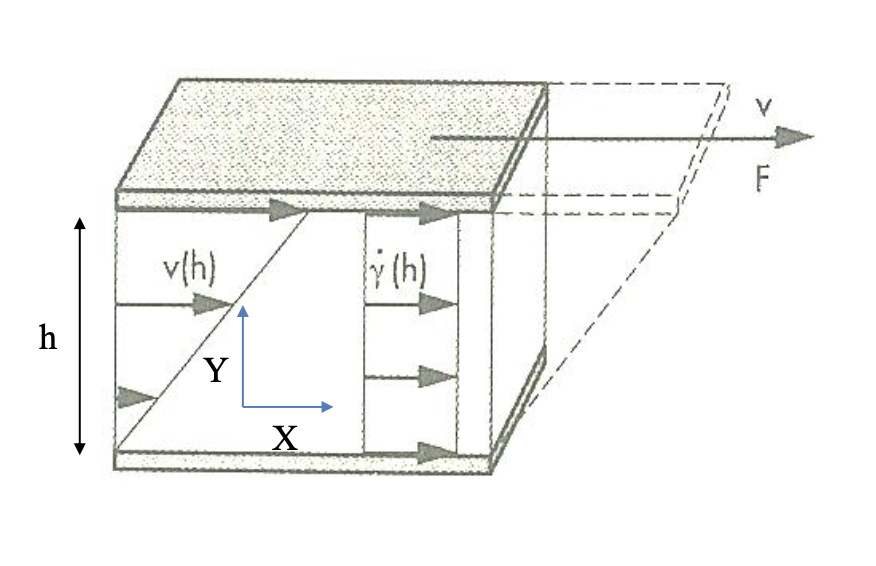
위 그림에서 가하게 되는 힘 $F$ 나 전단에 가하게 되는 속력 $v$ 를 조절할 수 있을 것이다. 그러면 $\tau$ (stress)나 $\dot{\gamma}$ (strain)을 control할 수 있을 것이고, 이를 기반으로 strain이나 stress를 측정할 수 있게 된다.

Capillary Rheometer

유체를 위에서 압력을 가하여 미세관을 통과시켜, flow rate를 측정하면 이를 기반으로 shear rate를 측정할 수 있다. 아래의 그림을 보자.

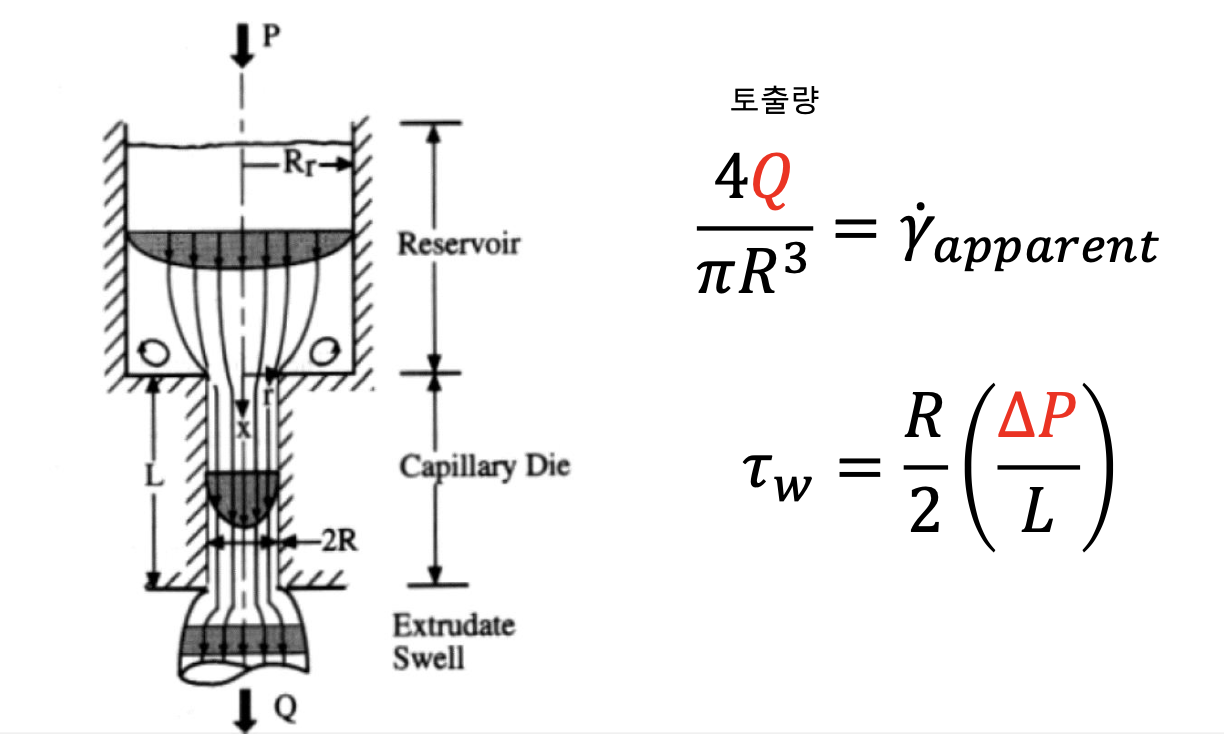
미세관(capillary die)를 통과하며 나오게 되는 토출량 $Q$ 를 통해 shear rate $\dot{\gamma}$ 를 측정할 수 있게 된다. 이때 다음과 같은 공식을 따른다.

\frac{4Q}{\pi R^3} = \dot{\gamma}_{\text{apparent}}

그런데 shear rate뿐만 아니라 stress도 측정할 수 있을 것이다. stress는 단위 면적 당 힘이였다. 이런 물리량을 갖는 것으로 압력( $P$ )이 있다. 그리고 다음과 같은 공식을 통해 유도할 수 있다.

\tau_w = \frac{R}{2} \left( \frac{\Delta P}{L} \right)

위에서 이야기한 원리로 capillary rheometer는 다음과 같은 2가지 모드를 통해 동작한다.

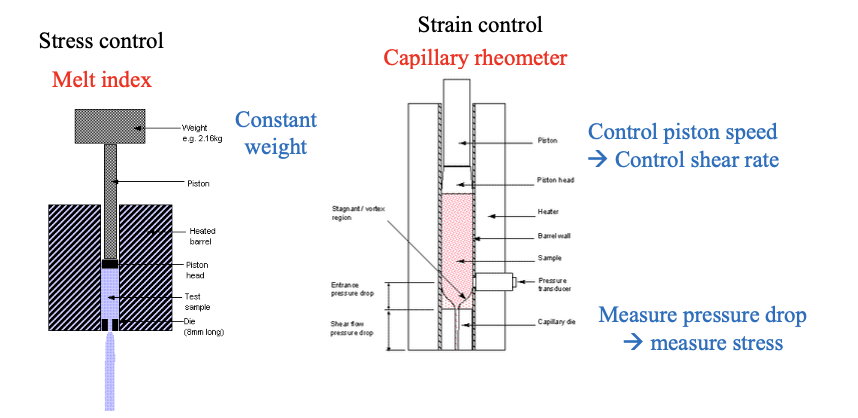
stress control의 경우에는 melt index를 사용한다. 위 그림의 왼쪽과 같은 경우로 일정한 하중을 가하여 stress를 control할 수 있다. 그러면 $\tau$ 는 constant한 값을 갖게 되고, 측정하게 되는 것은 strain rate가 된다. 그리고 이는 위에서 이야기한 토출량 $Q$ 를 기반으로 계산하게 된다. 일정한 stress $\tau$ 에 대해 높은 노출량 $Q$ 가 나오는 경우, strain rate $\dot{\gamma}$ 가 높아지고, 이는 점도 $\eta$ 가 낮다는 의미가 된다.

strain을 control하는 경우에는 capillary rheometer를 사용한다. 일정한 속도로 유체를 밀어내는 피스톤을 이용하여 strain rate를 control한다. 그러면 strain rate가 constant한 값을 갖게 되고, 측정하는 것은 stess, $\tau$ 이다. 다만, 위에서 이야기한 원리를 기반으로 압력을 측정하여 공식에 따라 stress를 측정하는 것이다.

Dynamic (Oscillatory) Rheometer

회전 레오미터는 [선형 점탄성] 05. 레오미터 의 글을 참고하자.
간단히 요약하면 회전을 통해 유동을 제어하는 레오미터를 의미한다. 회전형 레오미터는 stress와 strain 모두 control할 수 있지만, 주로 사용하는 것은 strain-controlled rheomoeter이다. 회전형 레오미터(strain-controlled rheometer)에서 점탄성 거동을 측정할 때 여러 fixture를 사용한다. 이는 시료의 종류에 따라 효율적인 실험을 하기 위함이다. 자세한 설명은 위 링크에 설명이 되어 있다.

Shear dependence of Viscosity

고분자 물질의 shear stress를 shear rate에 대해 측정해보면, 다음과 같은 그래프로 나타나진다. 위에서도 shear rate에 대한 stress의 변화에 따라 뉴턴 유체와 비뉴턴 유체로 구분을 하긴 했지만 아래 그래프는 좀 더 넓은 영역의 shear rate에 대해 측정한 것이다.

출처

위 그림을 보면 알 수 있지만, 낮은 shear rate에서는 고분자의 대부분의 분자들은 entangled state, 즉 entanglement가 일어난 상태이다. 그렇기에 flow에 의해 entanglement가 방해받고 풀리게 된다. 이 영역에서는 뉴턴 유체와 비슷한 거동을 보인다. 그러나 점점 shear rate가 높아지면서 entanglement density가 점점 줄어들게 되고 이에 대한 결과로 flow에 저항하는 능력, 점도도 마찬가지로 감소한다. 그러므로 shear thinning이 일어난다. 그러다 매우 높은 shear rate를 갖는 영역으로 가게 되고, 또 다시 새로운 entanglement가 일어나지 않는다를 상정하는 ideal case에서 뉴턴 유체와 같은 거동을 보이게 된다.

Constitutive Equation

고분자 물질로 shear rate에 대한 점도 $\eta$ 로 그래프를 그려봤을 때, 아래와 같은 결과를 얻을 수 있다.

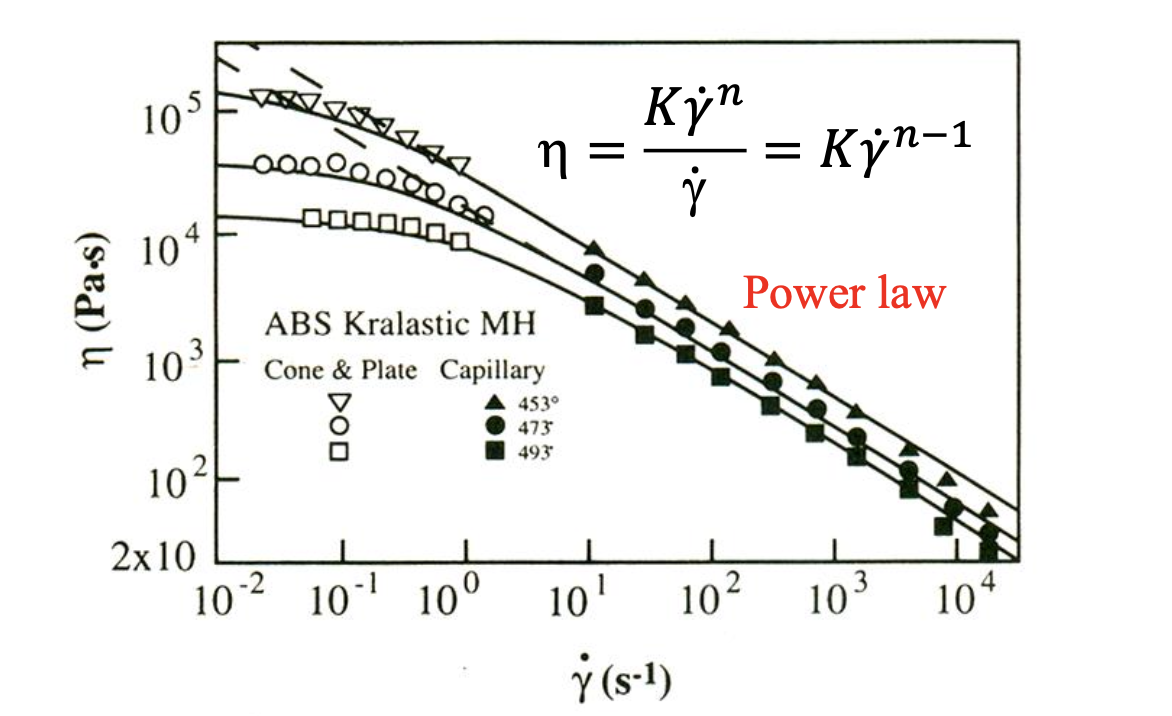
위 실험 결과로 구성 방정식이 다음과 같다는 결론을 내릴 수 있다.

\eta = \frac{K \dot{\gamma}^n}{\dot{\gamma}} = K \dot{\gamma}^{n-1}

즉, shear rate를 높임에 따라 점도가 낮아지는 shear thinning이 관찰되는 것을 알 수 있다.

Effect of Chain Length

또한 shear rate가 가해지지 않았을 때 측정되는 초기 점도( $\eta_0$ )는 chain length에 영향을 받는 것으로 밝혀졌다. 고분자 melt에는 상당한 entanglement가 존재하기에 다른 chains에 의해 어떠한 움직임은 제한되게 된다. 흐름이 존재하는 동안, 이러한 마찰(friction)과 entanglement에 의해 에너지의 소산(dissipation)이 일어난다. 이것이 점도로 측정되는데, 만약 chain의 길이가 너무 짧다면 entanglement effect로 부터 점도에 기여하지 못하게 된다. 하지만 특정 chain length를 넘게 되면 충분히 flow에 대해 저항할 수 있게 되어 점도가 비교적 높게 측정이 된다. 아래의 log scale로 그린 그래프를 보면, chain length가 증가함에 따라 일정하게 $\eta_0$ 의 기울기가 1이 되다가 특정 길이를 넘게 되면 3.4로 뛰는 것을 볼 수 있다. 이떄의 특정 chain length를 Critical Chain Length라고 한다.

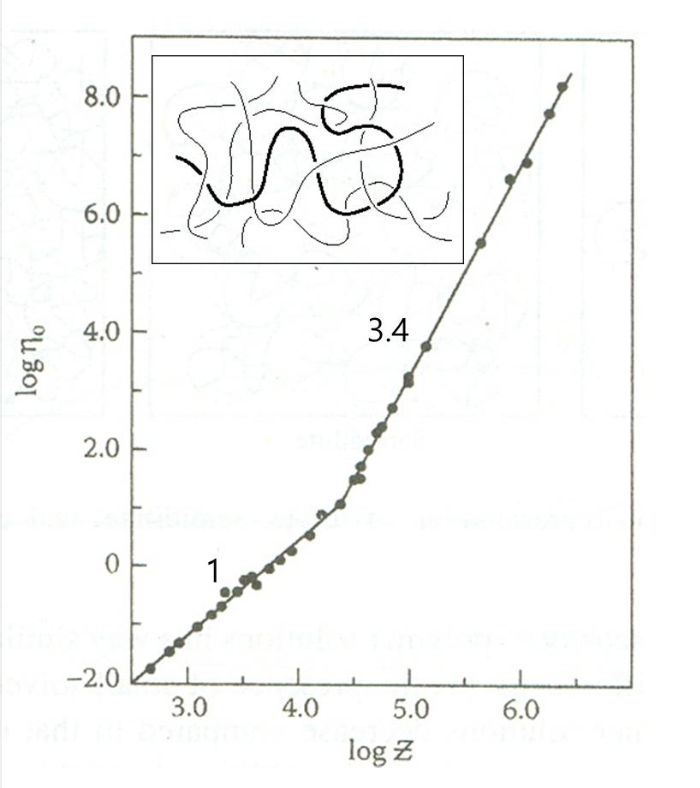
Mechanical Properties

흐름과 변형에 대한 정도를 측정하는 것이 중요한 이유는 기계적 물성과 연관지을 수 있기 때문이다.

Poission Ratio

우선 변형에 대한 부피의 변화가 없다는 가정하에 간단한 elongation mode를 생각해보자.

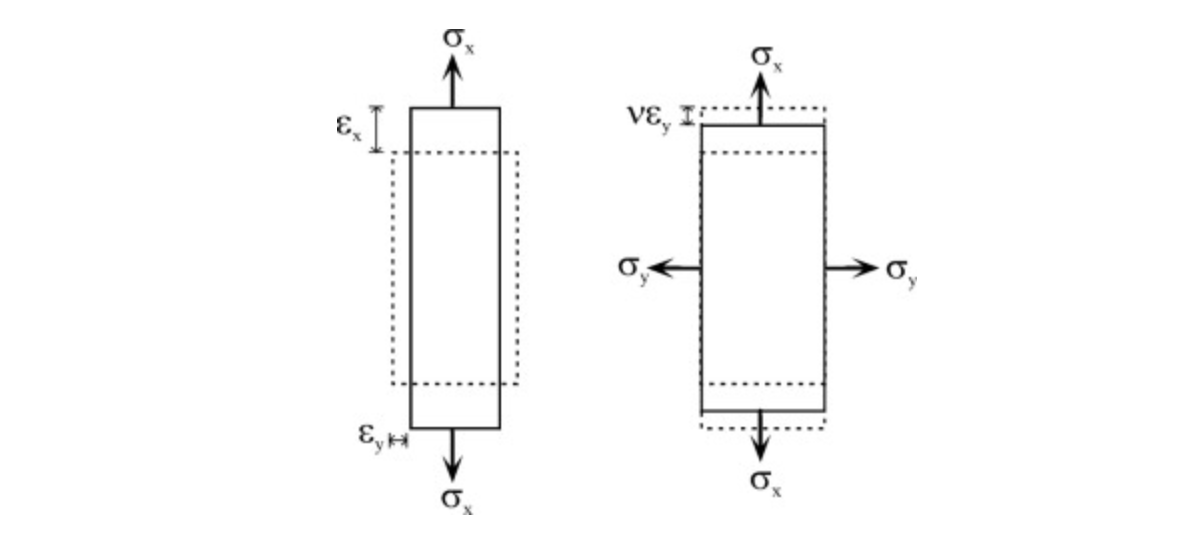
이때 Poisison's ratio는 다음과 같이 정의한다. 푸아송 비는 재료가 인장력의 작용에 따라 그 방향으로 늘어날 때 가로 방향 변형도와 세로 방향 변형도 사이의 비율을 나타낸다. (from wikipedia)

v_p = - \frac{d \varepsilon_{trans}}{d \varepsilon_{axial}} = -\frac{dy/y_0}{dx/x_0} \sim 0.5

부피의 변화가 없다는 가정하에 0.5로 근사되는 이유는 다음과 같다.

\begin{aligned} V = y^2 x \rightarrow dV &= 2ydyx + y^2dx =0\\ 2ydyx &=-y^2dx\\ \frac{dy}{y} &= -\frac{1}{2}\frac{dx}{x}\\ \frac{dy/y}{dx/x} &= -0.5 \end{aligned}

그렇다면 shear mode에서는 어떻게 될까(주의해야할 점은 shear mode는 유체에만 한정되는 것이 아니다.)? 아래의 그림과 같이 shear를 가하면,

그럼 elastic solid를 가정하면, Hook's Law에 의해 $\tau = G \gamma$ 를 따르기에, $G$ 는 다음과 같이 나타낼 수 있다. 여기서 $G$ 는 shear mode의 modulus, shear modulus가 된다.

G = \frac{\tau}{\gamma} = \frac{F /yz}{dx /y} = \frac{F/A}{\tan \theta} \approx \frac{F/A}{\theta}

마지막의 근사는 아주 작은 strain에 대해서만 성립한다. 또한 homogeneous isotropic material에 대해서 다음과 같이 Young's Modulus $E$ 와 shear modulus $G$ 를 연관짓는 관계식이 존재한다고 알려져 있다.

E = 2(1+ v_p) G

만약 압축되지 않는 탄성체(elastic solid)를 가정한다면, 부피 변화가 없다는 의미로 푸아송 비( $v_p$ )는 0.5가 된다. 그렇기에 이 경우에는 $E = 3G$ 가 된다. 그렇다면 Young's Modulus $E$ 는 무엇일까?

Strain Stress Curve

Young's Modulus는 고체 재료의 stiffness(강성)을 나타내는 지표이다. 본래 물체의 변형을 알아보기 위해 후크의 법칙( $F = kx)$ 에 따라 $k$ 를 물체의 종류와 물질의 모양까지 고려하여 하나하나 측정했어야 했다. Young's modulus는 선형적인 strain과 stress의 관계에 나타나는 탄성 계수로, 물체의 종류만 안다면 Young's Modulus $E$ 를 측정할 수 있었다. 여러 Plastic과 Elastomer에 대한 strain-stress curve는 다음과 같이 나타난다. 이때 선형적인 관계를 나타낼 때 기울기를 Young's Modulus라고 한다.

Testing Mode

고분자 물질의 점탄성 거동을 알아보기 위해 레오미터를 사용한다. 이때 strain을 control하냐 stress를 control하냐 혹은 레오미터에 가해지는 input을 어떠한 함수로 주어지냐에 따라 testing mode를 나눌 수 있다. 가해지는 input이 stress(측정하는 output은 strain이다.)이면 Creep & Recoil testing mode이다. 반면 input이 strain이면 Stress Relaxation testing mode와 Oscillation testing mode(dynamic test)가 있다. oscillation testing mode의 경우에는 creep & recoil과 stress relaxation과 다르게 sinusodial function으로 input이 주어진다.

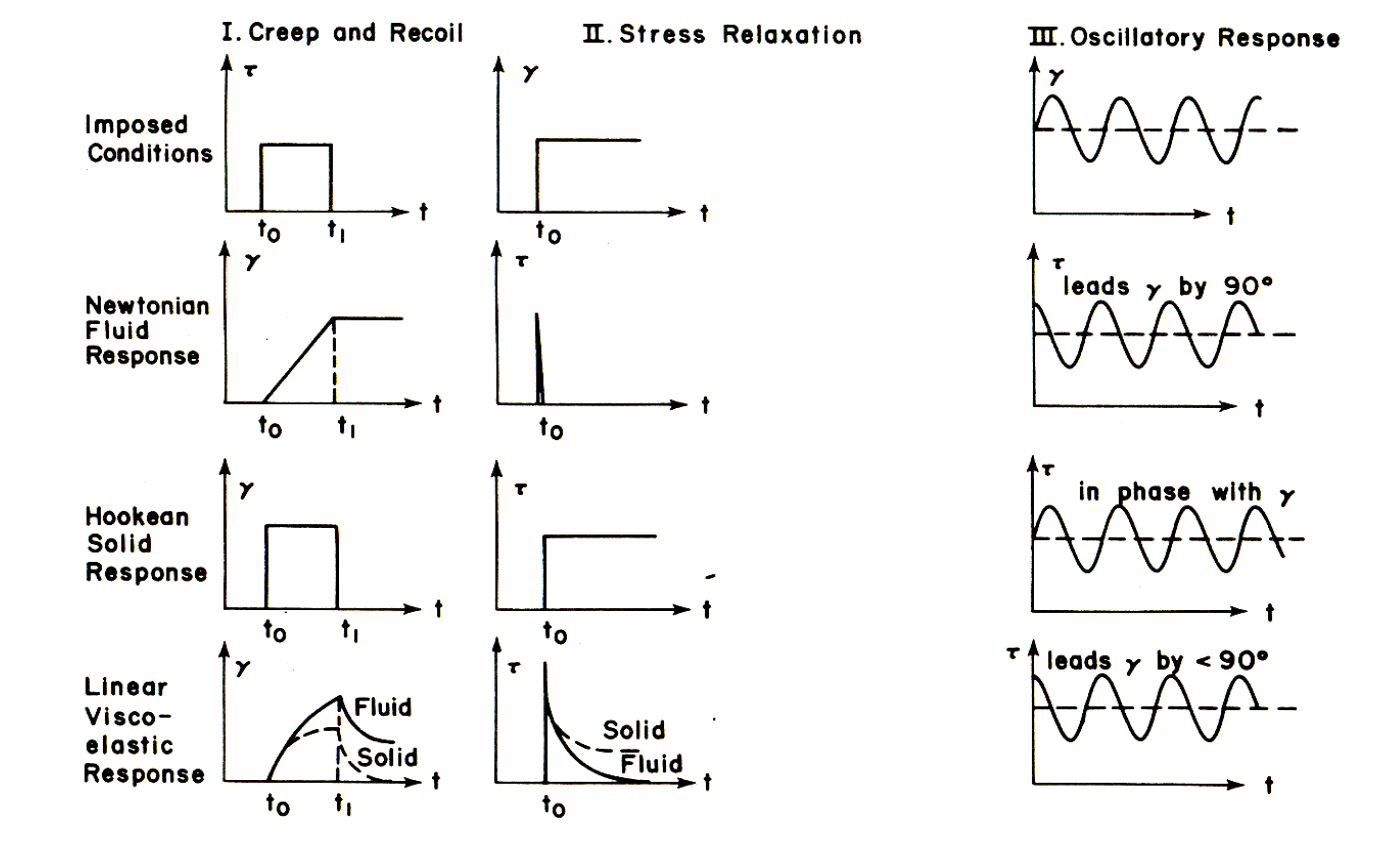
Creep & Recoil

위 그림의 좌측이 Creep & Recoil testing mode를 뉴턴 유체 / hookeon solid / 선형 점탄성 물질에 따라 어떻게 측정되는 지를 살펴본 것이다. 우선 뉴턴 유체의 경우에는 뉴턴의 유체 법칙에 따라 $\eta = \eta \dot{\gamma}$ 를 따르기에 unit step function으로 stress을 input으로 가했을 때, 측정되는 strain은 다음과 같이 표현할 수 있다.

\tau = \eta\dot{\gamma} \rightarrow \tau_0 = \eta\dot{\gamma}\\ \gamma = \frac{\tau_0}{\eta} t

시간에 따른 일차함수로 나타나는 부분이 stress를 input으로 주는 $[t_0, t_1]$ 구간에서 나타날 것이다. 반면 Hookean solid의 경우에는 후크의 법칙에 따라 $\tau = G\gamma$ 이기에 같은 개형이지만 측정되는 strain, $\gamma$ 는 다음과 같을 것이다.

\gamma = \frac{\tau}{G}

그렇다면 점탄성을 띄는 물질의 경우 어떻게 strian이 측정될까?

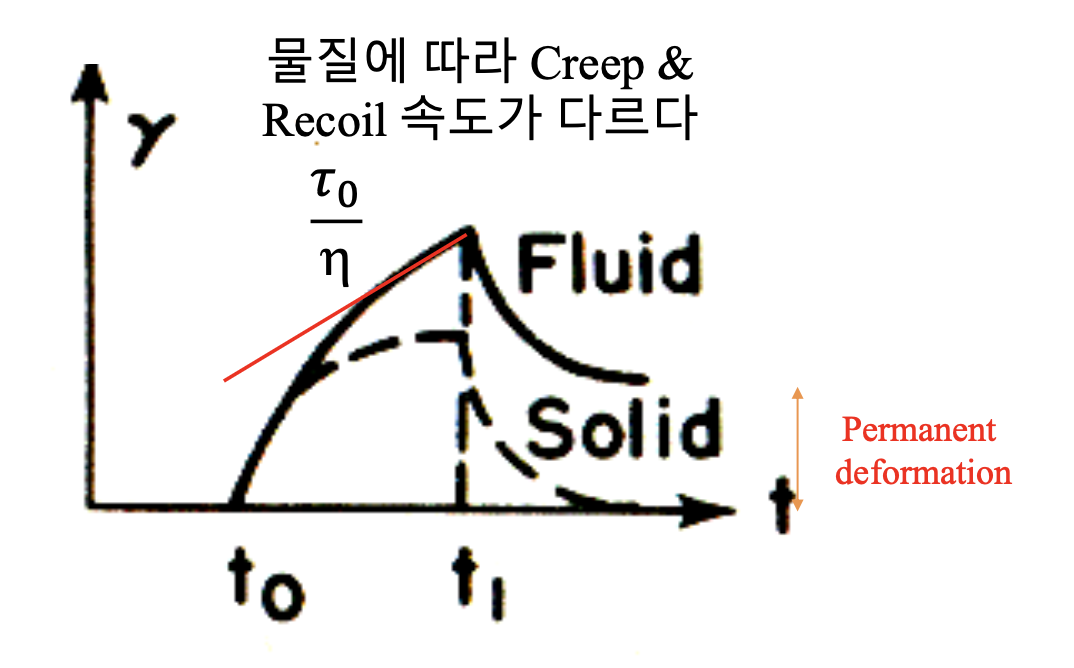
우선 물질에 따라 creep & recoil되는 속도가 다르다. 점탄성을 띄기에 stress를 구간 $[t_0, t_1]$ 에 가했을 때 에너지가 소산되며 $t_1$ 에 가까워질 때 측정되는 strain의 기울기가 뉴턴 유체의 $\tau_0 / \eta$ 에 가까워진다. $t_1$ 이후에는 에너지가 저장되는 탄성의 성질이 나타나는데 solid의 경우에는 strain이 0에 수렴하지만, fluid의 경우에는 0에 수렴하지는 못하고 permanent deformation이 나타나는 것을 확인할 수 있다.

Stress Relaxation

stress relaxation testing mode는 strain을 input으로 가한다. 또한 가해지는 input 함수의 개형이 unit step function이기에 유체의 경우, 뉴턴 유체 법칙에 따라 $\tau = \eta \dot{\gamma}$ , 측정되는 stress $\tau$ 는 디렉 델타 함수가 된다. 즉, $t_0$ 에서 peak를 띈다. 뉴턴의 유체 법칙에 따라 $\tau$ 가 $\gamma$ 의 미분에 $\eta$ 를 곱한 값이 된다. unit step function에서 $\gamma$ 를 미분한 $\dot{\gamma}$ 는 $t_0$ 에서는 무한대가 되고 그 이후에는 0이 되기 때문이다. 반면 고체의 경우에는 creep & recoil과 동일하게 같은 개형의 stress가 측정될 것이다. 그렇다면 점탄성 물질은 어떻게 될까?

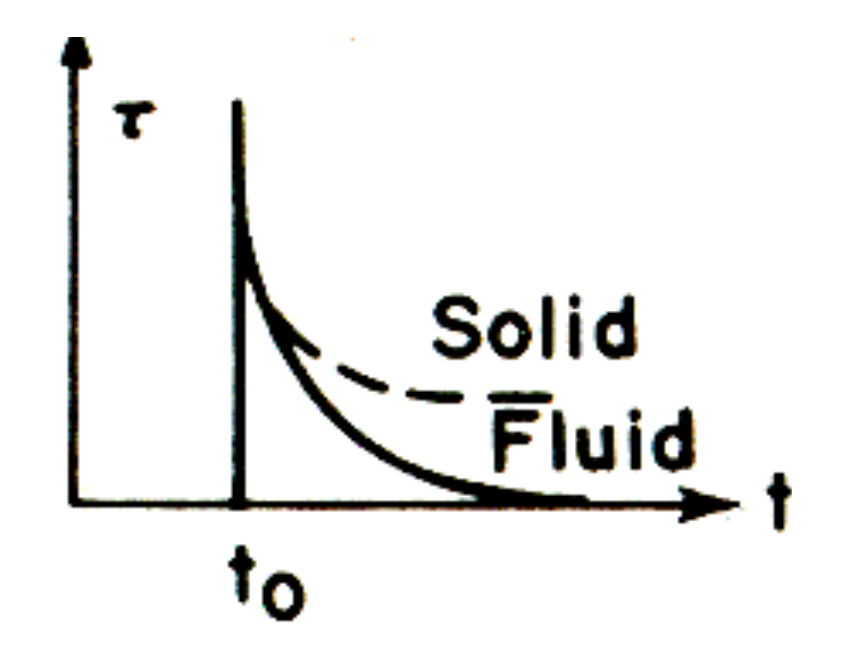
물질에 따라 relaxation 속도가 달라지는 것을 확인할 수 있다. 고체의 경우에는 0에 수렴하지 못하지만, fluid의 경우에는 0에 수렴한다.

Oscillation

oscillation의 경우에는 가해진 input 함수의 개형이 sinusodial function(정현파 함수, 간단히 sin 함수라고 생각하자)이다. 또한 control하게 되는 input은 strain이기에 다음과 같이 $\gamma$ 를 표현할 수 있다.

\gamma = \sin\omega t

여기서 $\omega$ 는 당연히 주기가 된다. 그러면 solid의 경우에는 후크의 법칙에 따라 $\tau = G\gamma$ 이므로 다음과 같이 측정된다.

\tau = G \sin \omega t

liquid의 경우에는 뉴턴의 유체 법칙에 따라

\dot{\gamma} = \omega \cos \omega t \rightarrow \tau = \eta \omega \cos \omega t

가 될 것이다.

점탄성 물질의 경우에는 다음과 같다.

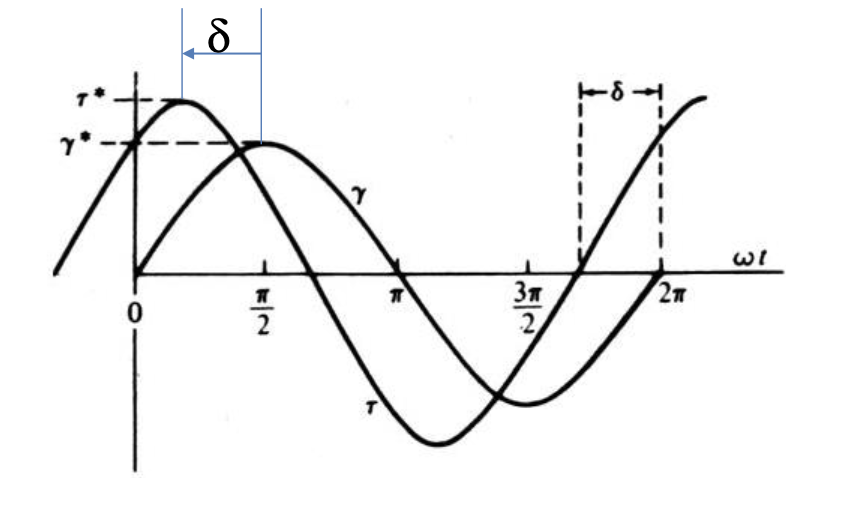
앞에서 creep & recoil과 stress relaxation을 보면서 알 수 있었던 점은 '점탄성'이라는 단어에서 확인할 수 있듯, 에너지를 저장하는 탄성과 에너지를 소산시키는 점성의 두 성질이 섞인 듯한 거동이 그래프의 개형에서 확인할 수 있었다. oscillation의 경우에도 비슷하다. 다만, 위 그림과 같이 위상 차가 나타나게 된다. 이를 일반화한 공식은 다음과 같다.

\tau = \tau_0 \sin (\omega t + \delta)

$\delta$ 값만큼 위상차가 나타나게 된다. oscillation testing mode, dynamic test의 측정 결과로 알 수 있는 점은 다음시간에 이어서 확인해보도록 하자.

jmt

고분자/컴공

다음 포스트

[고분자 물리] Viscoelastic Properties