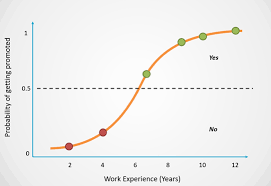
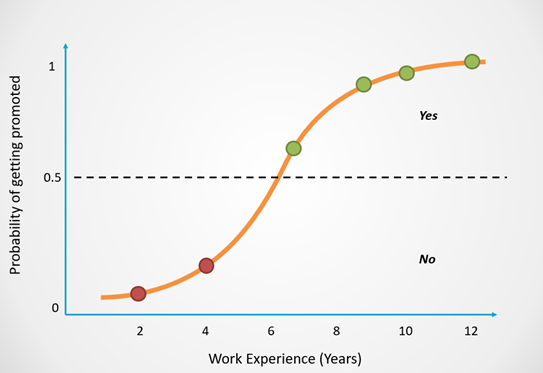
1. Logistic Regression

• regression이지만 회귀가 아니라 분류 모델이다.
• logistic regression은 간단하지만 선형모델에서 강력한 성능을 보여주낟.

Odd Ratio

$odds\,\,ratio = \frac{P}{1-P}$ (P is positive probility)

• odd ratio(이상 비율)는 $positive\ratio{nagative}$ 비율을 나타내는 식이다.
• 값이 크면 positive일 확률이 높은 그룹일 것이다.

Log Odd Ratio

$logit(P) = log\frac{P}{1-P}=log\frac{P}{1-P}$

$Logit(P(y=1|X))=w_0x_0+w_1x_1+...+w_mx_m=\Sigma^{m}_{i=0}=W^TX$

• $P(y=1|X)$는 input이 $X$(vector)일때 y=1일 확률을 나타낸다.
• 즉, 특정 input에 대해서 positive label일 확률(이진 분류라고 가정했을때)을 나타낸다.
• 그 확률을 input $X$의 weight sum으로 표현한것이 $logit(P)$이다.

$\therefore{logit\frac{P}{1-P} = W^TX=Z}$
$\quad log\frac{P}{1-P}=Z$
$\quad e^z=\frac{P}{1-P}$
$\quad e^z(1-P)=P$
$\quad e^z-e^zP=P$
$\quad e^z=P(1+e^z)$
$\quad P=\frac{e^z}{1+e^z}$
$\quad P=\frac{1}{1+e^{-z}}$

• 이 식을 보면 막막할 수 있다. 하지만 천천히 살펴보자
• 우리는 input $X$를 알 수 있다. $W$는 학습되는 값이므로 초기값이 임의로 정해지기 때문에 알 수 있다.
• 우리는 우리에게 선천적으로 주어진 X를 활용하여 y=1일 확률을 예측하고 학습용 데이터에서 실제로 X일때 y=1일 확률이 얼마나 되는지 확인하여 그 차이를 학습한다.

$\Phi(Z)=P=\frac{1}{1+e^z}$
$z=W^TX$

로지스틱 비용 함수의 가중치 학습

$J(W) = \Sigma^{n}_{i=1}[-y^{(i)}log(\Phi(Z^{(i)}))-(1-y^{(i)}log(1-\phi(Z^{(i)})]$

이 식은 로지스틱 회귀 모델의 비용함수이다. 식의 모양이 아래의 일반적인 비용함수와는 조금 달라보인다.

$J(W) = \frac{1}{2}\{\Sigma_{j}y^{(i)}-\Phi(Z^{(i)})\}^2$

이제부터 왜 이런 차이가 나는지 확인해보자.

Likelyhood L

• 데이터셋의 각 데이터가 독립이라고 가정했을때

$L(W)=P(y|X;W)$
$\qquad \;\;\;=\Pi^n_{i=1}P(y^{(i)}|X^{(i)};W)$
$\qquad \;\;\;=\Pi^n_{i=1}(\Phi(Z^{(i)})^{y^{(i)}}(1-\Phi(Z^{(i)}))^{1-y^{(i)}}$

Likelyhood, 가능도라고 부르는 이 식은 현재 내가 정답을 맞출 확률이 얼마나 되는지를 표현하는 식이다. $L(W)$에서 parameter가 W만 있는 이유는 우리가 바꿀 수 있는 값이 W뿐이기 때문이다. X와 Y는 이미 정해진 데이터이다. 우리는 W를 조정하여 X(input)을 받았을때 y를 잘 예측하면 된다.

이제 마지막 식을 보자. 식이 y=1인경우와 y!=1인 경우로 나눠놨다. 즉, W를 잘 조정하여 X잘 곱해서 y=1인 경우를 최대한 많이 맞추고, y!=1인 경우도 최대한 많이 맞춘다면 likelyhood의 값이 최대가 될 것이다. 왜냐하면 두개의 가능성이 최대가 되었으니 그 곱이 최대가 되기 때문이다.

$l(W) = log(L(W))$
$\qquad \;\; = \Sigma^{n}_{i=1}[y^{(i)}log(\Phi(Z^{(i)}))+(1-y^{(i)}log(1-\phi(Z^{(i)})]$

위 likelyhood에서 log를 씌운것이다. 이 식은 답을 잘 맞출수록 값이 커지도록 되어있다. 즉, 학습 목표가 함수값을 최대화 하는데 있다. 하지만 값을 최대화 하는것은 어느정도가 최대인지 알기가 어렵다. 경사하강법으로 최소값을 찾기 위해서 우리가 위에서 봤던 비용함수처럼 식에 -1을 곱해준다.

$J(W) = \Sigma^{n}_{i=1}[-y^{(i)}log(\Phi(Z^{(i)}))-(1-y^{(i)}log(1-\phi(Z^{(i)})]$

Why Log?

• 가능도가 매우 작을 때 발생하는 수치상의 언더 플로우를 미연의 방지
• 계수의 곱을 합으로 변경가능
• 미분이 쉽다.

지금까지 Logistic Regression에 대해서 알아봤다. 다음장은 다른 분류 모델중 하나인 SVM(Support Vector Machine)에 대해서 알아보자.

참고자료

• https://www.natasshaselvaraj.com/logistic-regression-explained-in-7-minutes/