3장 분류모델(3) Decision Tree(결정 트리)

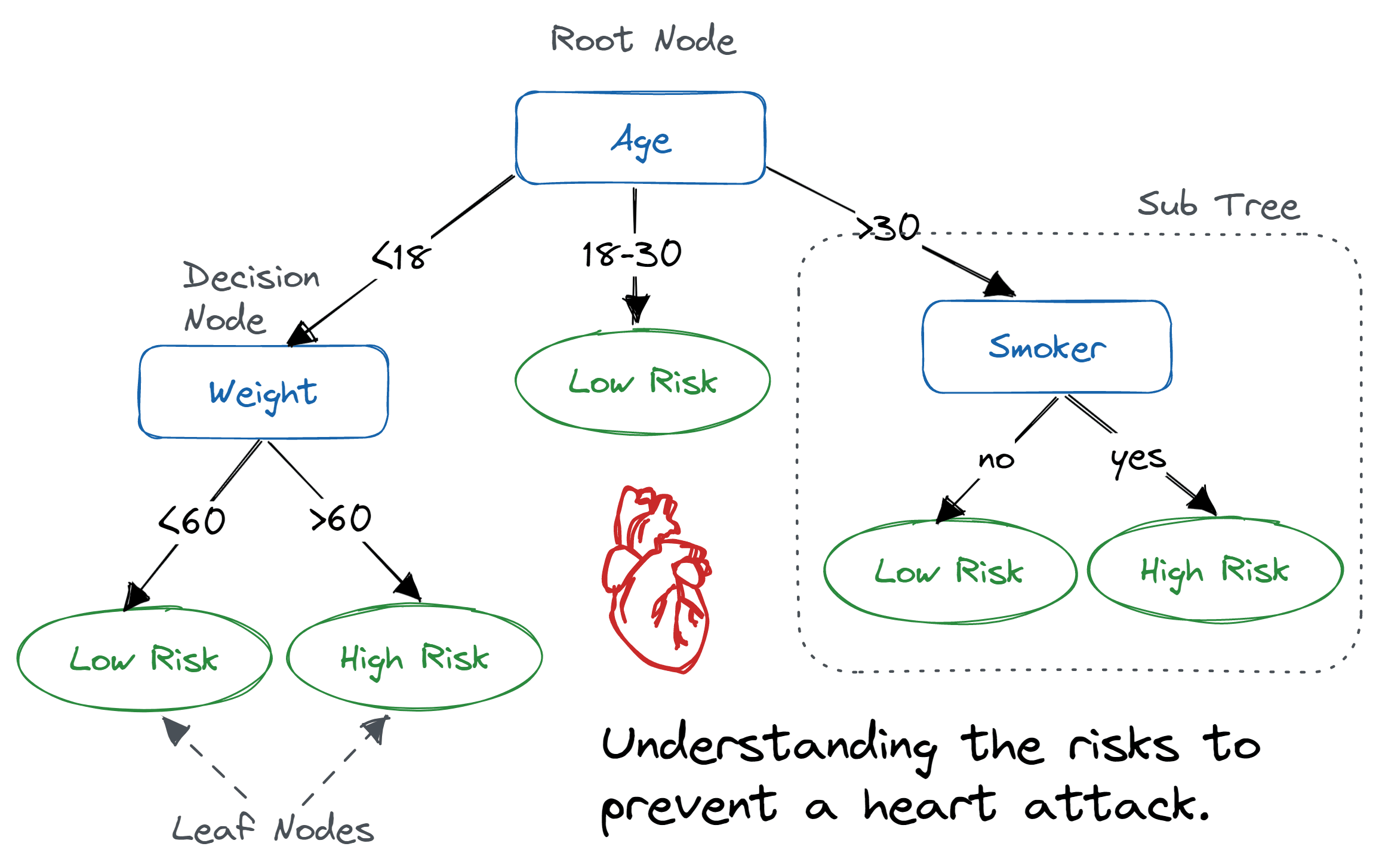
Decision Tree, 결정 트리

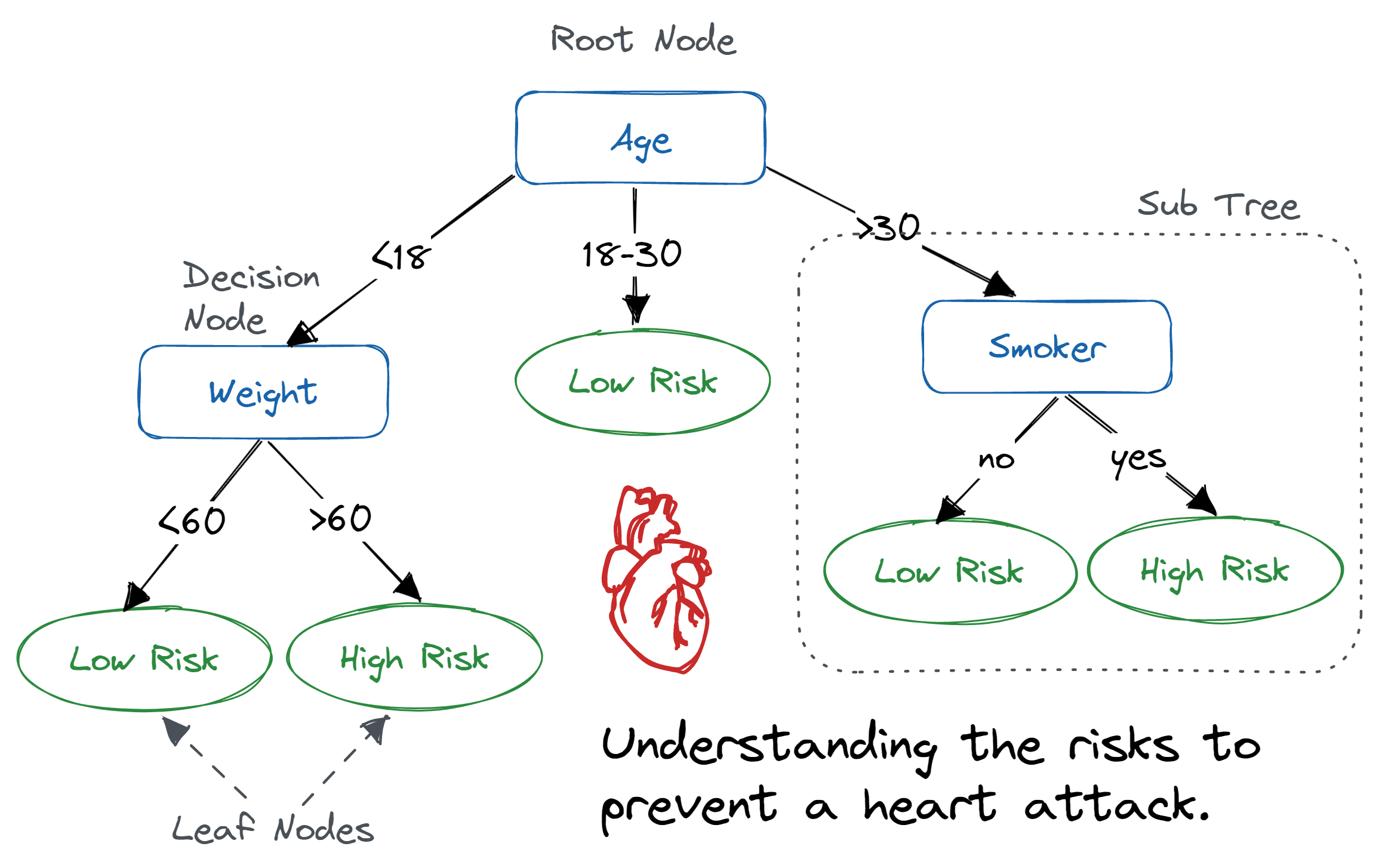
• feature를 기반으로 클래스의 lable을 cnwjd
• 범주형/연속형 데이터 모두 가능
• tree root부터 시작하여 information Gain(정보이득)이 최대가 되는 특성으로 데이터를 나눈다.
• 과적합을 막기 위해 treedepth를 제한

정보이득 최대화

$IG(D_p, f) = I(D_p) - \Sigma_{j=1}^{m}\frac{N_j}{N_p}I(D_j)$
$IG(D_p, f) = I(D_p) - \frac{N_{left}}{N_p}I(D_{left}) - \frac{N_{right}}{N_p}I(D_{right})$

f : 분할에 사용될 특성
$D_p$ : 부모 데이터셋
$D_j$ : 자녀 데이터셋
$N_{p,n}$ : 부모 혹은 자녀 샘플 개수

이진 결정트리에 널리 사용되는 세 개의 불순도 지표

1. Gini impurity, $I_G$
2. Entropy, $I_H$
3. Calssification Error, $I_E$

1과2는 비슷하다.

entropy

$p(i|t) != 0$

i : class i에 속한 sample ratio
t : t번째 node
전체 샘플에 대해서 entropy를 구했을때 0이라면 모든 샘플의 class가 같다는 뜻이므로 분류할 필요가 없음. 즉, 전제가 될 수 없음

Entropy, $I_H$

$I_H(t) = - \Sigma^{c}_{i=1}p(i|t) \log_{2}p(i|t)$

• 특정 t번째 노드에서 모든 샘플이 같은 클래스면 엔트로피는 최소가 된다.
  -> 즉, 분류가 잘 되면 값이 최소가 됨
• 반대로 모든 샘플에 대해서 클래스의 분산이 반반이라면 엔트로피는 최대가 된다.
  -> 즉, 분류가 잘 안 되면 값이 최대가 됨

Gini Impurity, $I_G$

$I_G(t) = \Sigma^{c}_{i=1}p(i|t)(1-p(i|t))=1-\Sigma^{c}_{i=1}p(i|t)^2$

$p(i|t)(1-p(i|t))$ i=1 또는 i!=1인 비율 곱

• 반반이면 최대가 된다.
  ex) 0.5 x 0.5 = 0.25 -> 최대
  반대로 0.999 x 0.001 = 0.000999 -> 최소 (실제로 최소는 아니지만 0.001을 최소라고 한다면)

Classification Error, $I_E$

$I_E = 1 - max\{P(i|t)\}$

t 번째 노드에서 분류가 제일 안 된 노드의 비율을 1에서 빼서 오차가 얼마나 되는지 확인

랜덤 포레스트 - 앙상블

랜덤 포레스트는 여러개의 결정트리를 만들어 평균을 낸다. 그렇게 했을때 일반화 성능이 높아지고 과대적합의 위험을 줄일 수 있다.

1. n개의 랜덤 부트스트랩(중복허용) 샘플을 고른다.
2. 샘플에서 결정나무를 학습한다.
   a. 중복x d개의 feature 선택
   b. 학습
3. 1~2 반복
4. 각 트리의 예측을 모아서 다수결로 결정한다.

장점
1. 하이퍼 파라미터 튜닝을 적게 해도 된다.
2. 가지치기를 할 필요가 없다.
3. 트리가 많을수록 성능이 올라가고 비용도 증가한다.

단점
1. 해석이 결정트리에 비해 상대적으로 어렵다.

참고자료

• https://www.datacamp.com/tutorial/decision-tree-classification-python