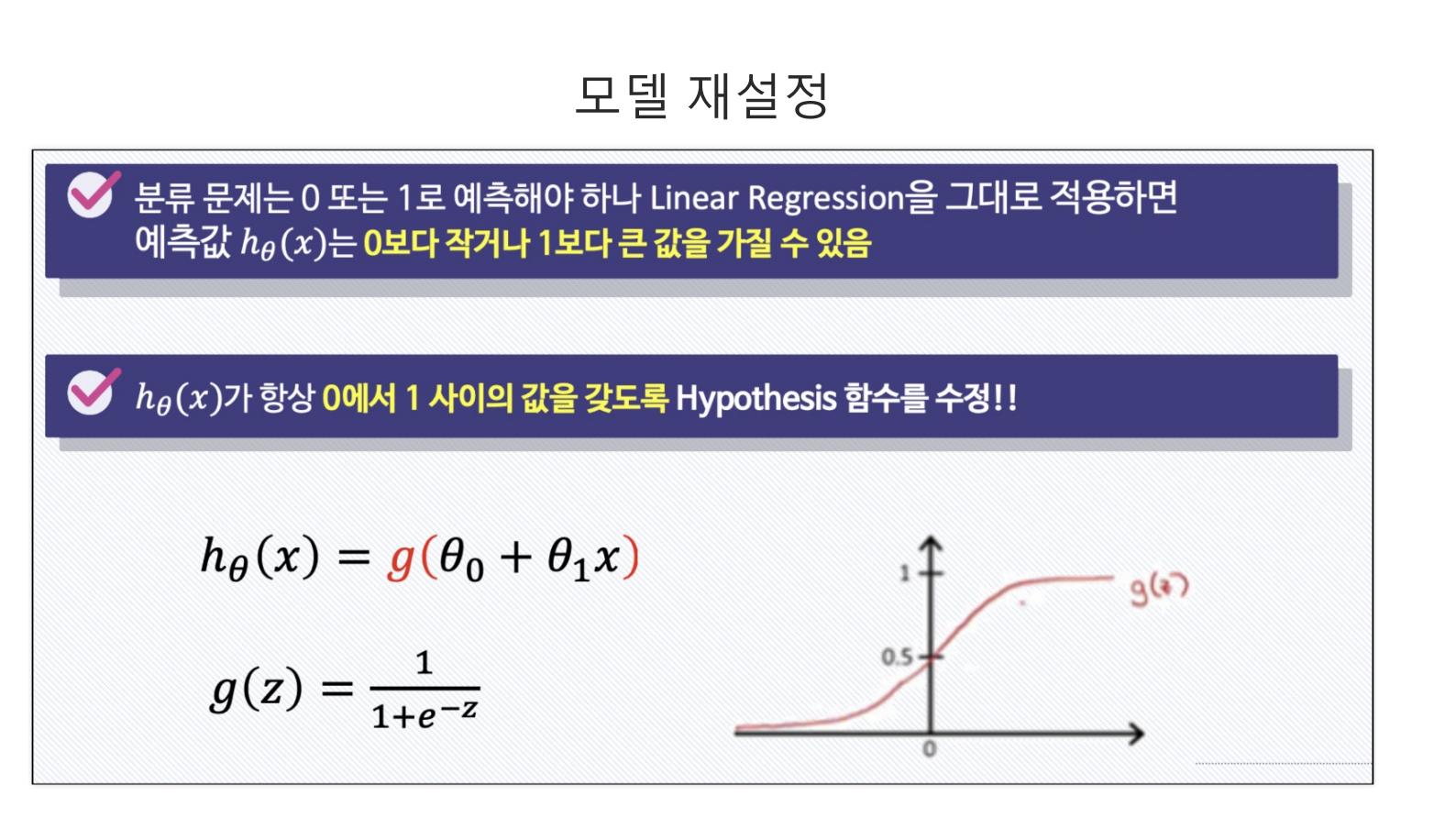
Logistic_Regression

안선경·2023년 3월 16일
0

ML_study

목록 보기
13/25

  • Logistic Regression모델은 결과값이 0과 1사이에서만 나와야 할 경우 사용하는 모델링 방법이다.
  • 이를 위해 사용하는 것이 시그모이드다. 시그모이드는 어떠한 입력값을 받아도 결국 0과 1사이에서 값을 출력하기 때문이다.
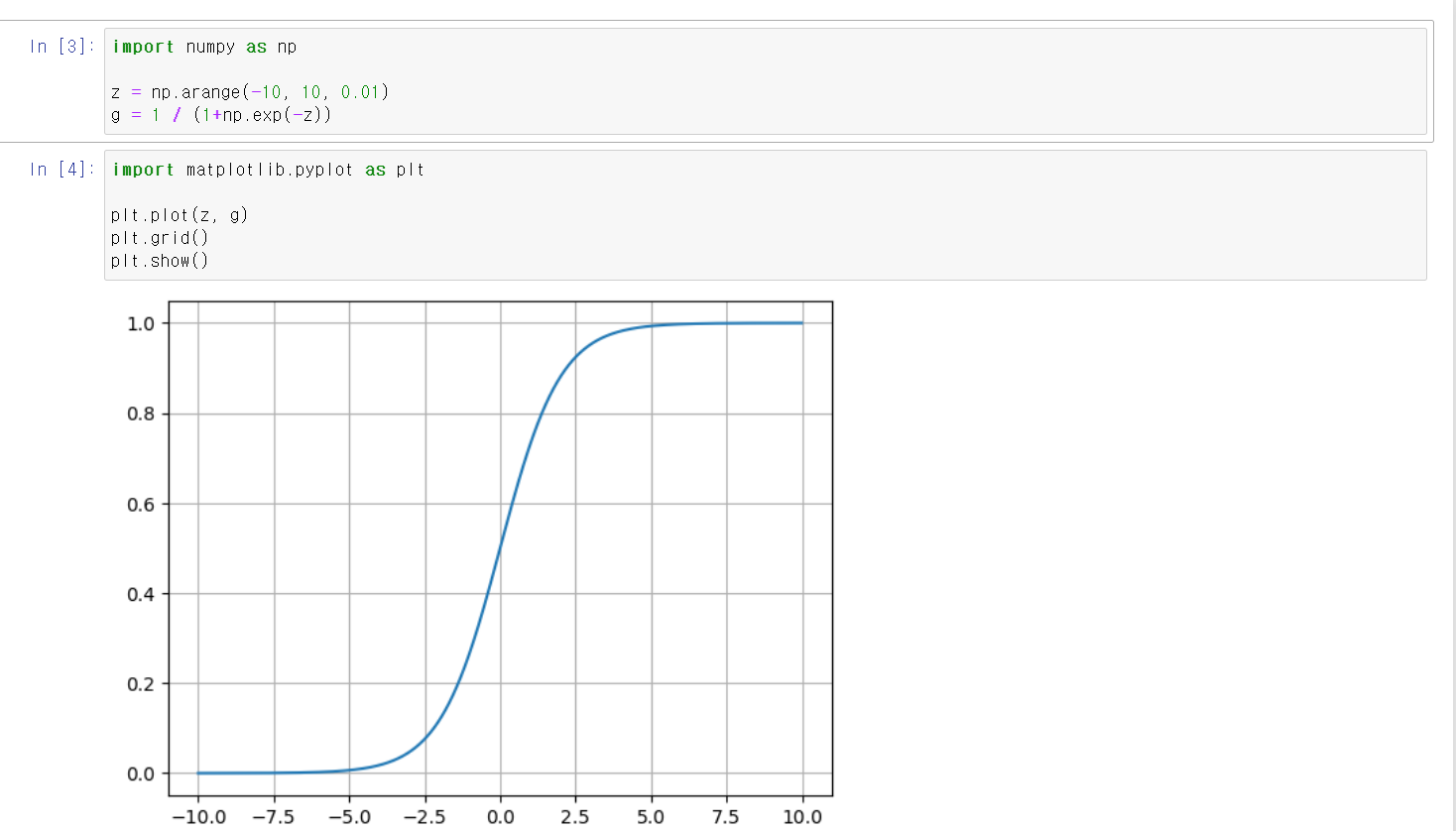
  • 임의의 숫자를 zz변수에 저장하고 11+e−z\frac{1}{1+e^{-z}}함수에 넣어서 시각화 결과 yy값 즉 출력값이 0과 1사이에서 나타난다.
  • 중요한 부분은 아니지만, 이런식으로 만들면 조금 더 있어 보인다.
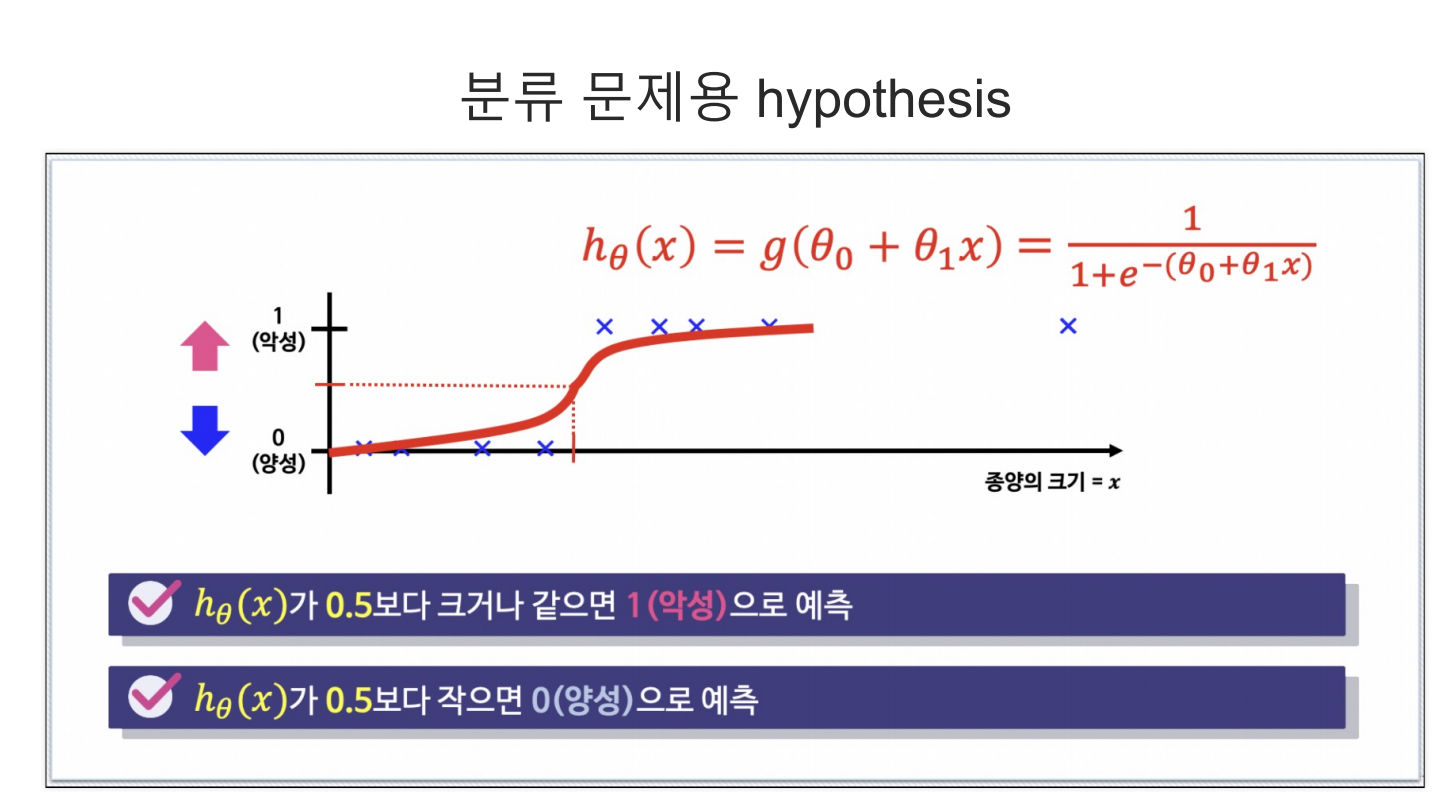
  • 출력한 값에 thresholds 값을 설정하고 기준에 따라 참값, 거짓값으로 구분할 수 있다.
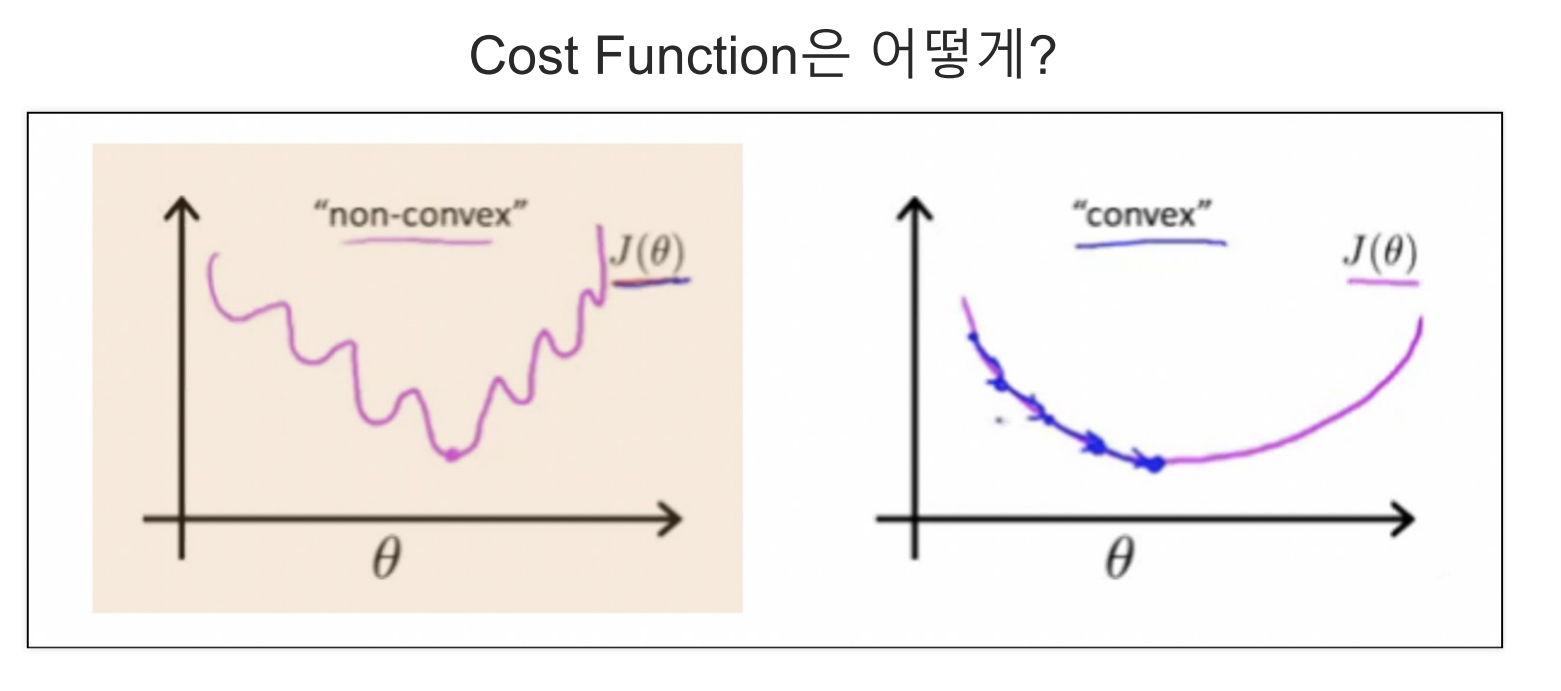
  • Ligistic Regression의 경우 Cost_Function을 기존의 방법으로 구할 수 없다.
  • 2차 함수의 모양이 구불구불하기 때문에 local_min지점에서 최소값으로 추정하여 global 최소값을 구할 수 없기 때문이다.
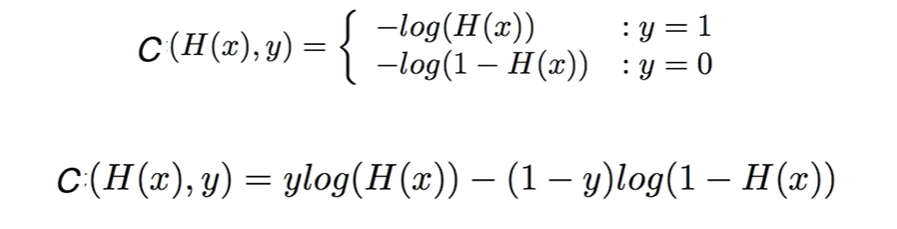
  • 그렇기에 해당 공식을 사용해서 yy의 값에 따라 두 가지 공식을 사용한다.
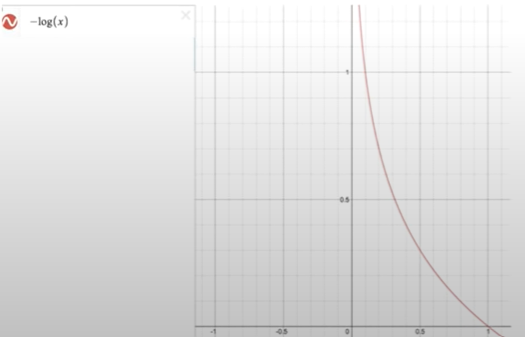
  • yy실제값이 1일 경우 위에 log그래프(−logx-logx)를 사용하는데,
    1. H(x)H(x)예측값이 1일 경우 예측값과 실제값이 일치하기 때문에 0에 가까운 값을 나온다
    2. H(x)H(x)예측값이 0일 경우 예측값과 실제값이 일치하지 않기 때문에
      ∞\infty에 가까운 값이 나온다
      -
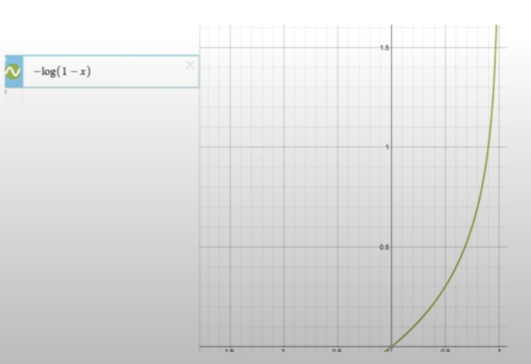
  • yy실제값이 0일 경우 log그래프(−log(1−x)-log(1-x))를 사용하는데,
    1. H(x)H(x)예측값이 0일 경우 예측값과 실제값이 일치하기 때문에 0에 가까운 값을 나온다
    2. H(x)H(x)예측값이 1일 경우 예측값과 실제값이 일치하지 않기 때문에
      ∞\infty에 가까운 값이 나온다
  • 하지만, 조건문을 사용할 경우 머신러닝, 딥러닝에서 사용하지 어려운 경우가 발생하기 때문에 하나의 식으로 정리할 수 있다.

    C:(H(x),y)=−ylog(H(x))−(1−y)log(1−H(x))C:(H(x),y) = - ylog(H(x)) - (1-y)log(1-H(x))

    y가 1일 경우 -> −log(H(x))-log(H(x))
    y가 0일 경우 -> −log(1−H(x))-log(1-H(x))

  • 이제 실제 데이터를 가지고 측정해보자
  • 항상 사용하는 wine데이터를 가지고 LogisticRegression에 fit시킨다.
  • 성능은 74% 정도로 결과값이 나온다
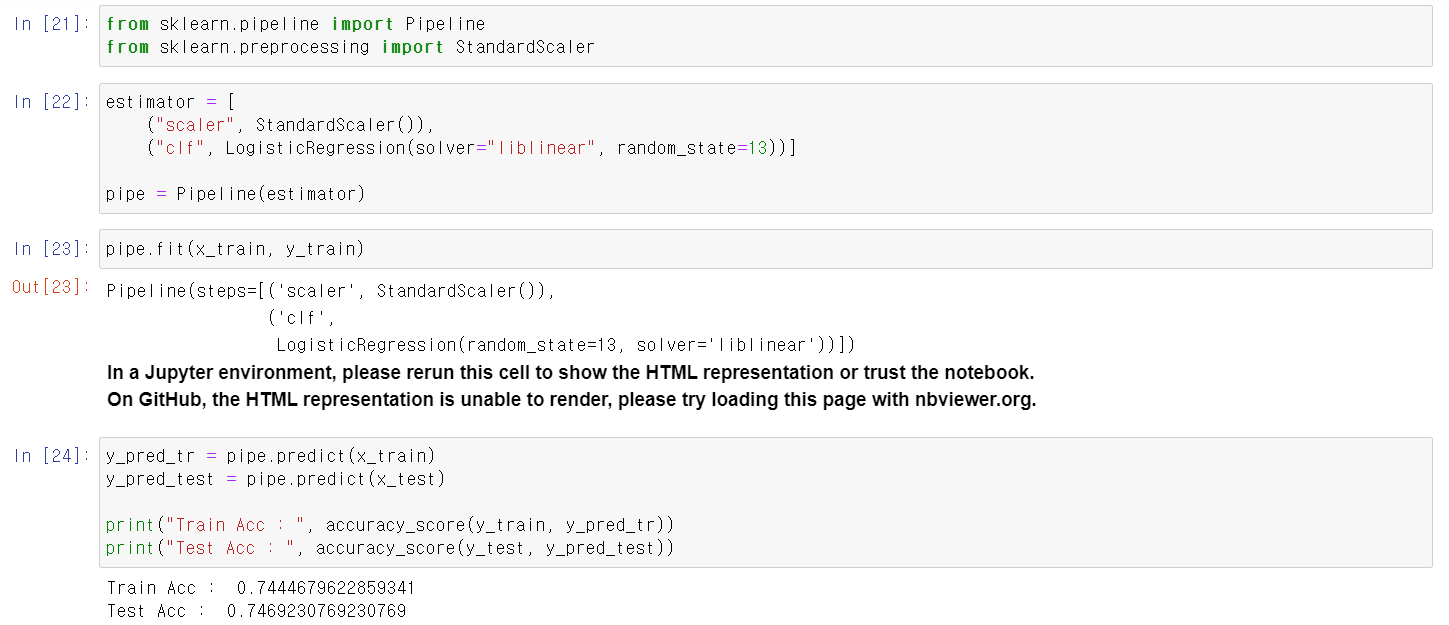
  • PipeLine으로 정규분포값으로 변환 후 다시 한 번 fit시킨다.
  • 결과값의 차이는 크게 없다.
  • 이번에는 DecisionTreeClassifier로 모델링을 했다.
  • 두 모델링의 결과를 딕셔너리 형태로 저장
  • pred 변수에 1이 될 확률 값을 저장하고, 실제 Label값과 성능을 테스트했다.
  • 성능값을 roc_curve로 fpr, tpr, thresholds의 각각의 값에 저장 후
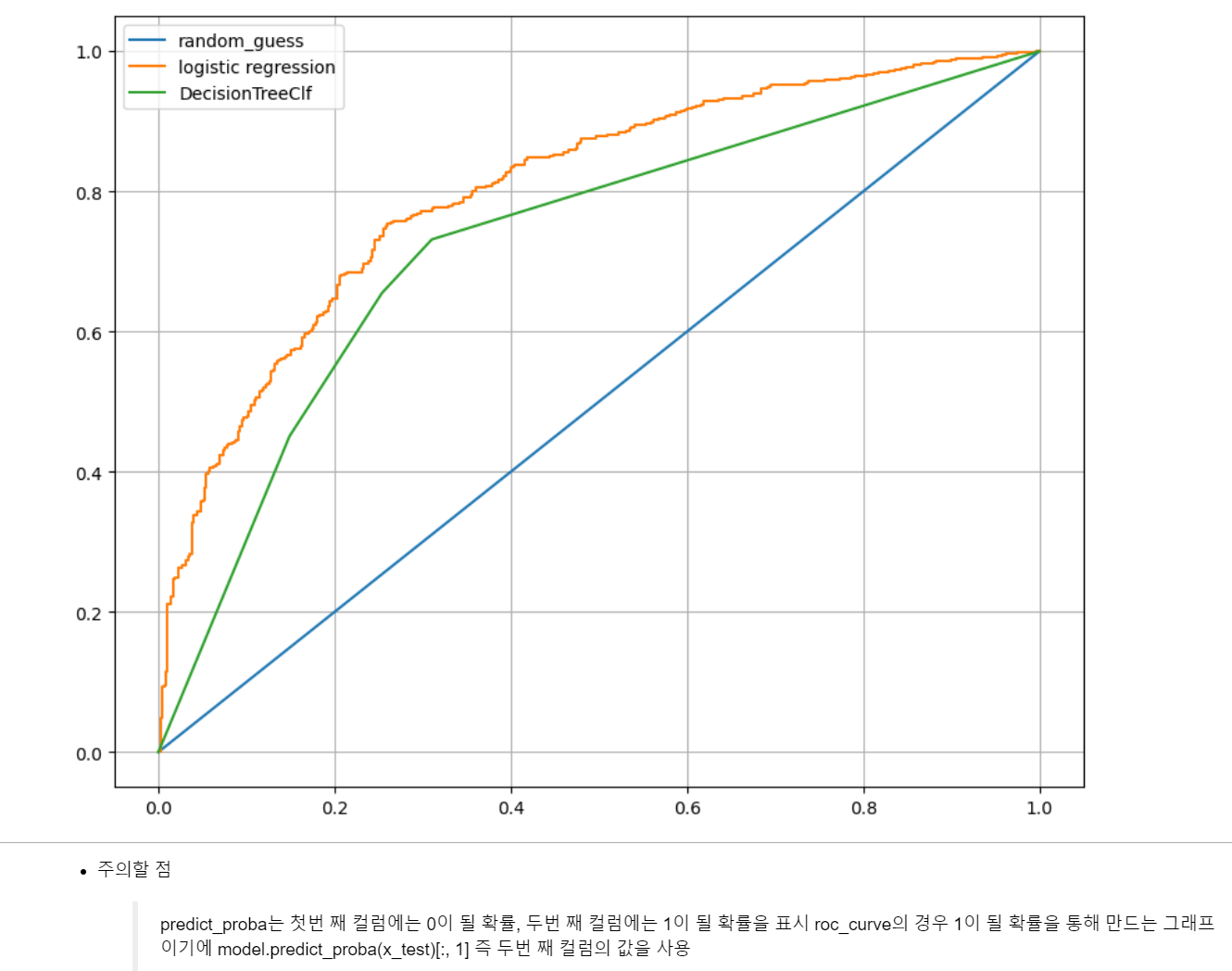
  • DecisionTree보다 logisticRegression이 더 높은 ROC값이 나온다.
profile
안선경
상황을 바꿀 수 없다면, 나를 바꾸자
이전 포스트

12. cost_function

다음 포스트

angsangbeul

0개의 댓글