[NLP | TIL] Negative Sampling과 Hierarchical Softmax, Distributed Representation 그리고 n-gram

Efficient Estimation of Word Representations in Vector Space 논문을 해석하던 중에 해당 개념들이 나와서 정리하게 되었다. 논문에서 빈번하게 등장하기도 하고 중요한 개념이라 생각된다.
논문에 대한 포스트는 다음 주말 중으로 올릴 계획이다.

💡 Negative Sampling

Word2Vec에서 사용되는 Negative sampling은 단어에 대한 학습을 보다 효율적으로 하기 위해서 고안된 방식이다. 우리가 학습시켜야 하는 Corpous는 몇 억개를 넘어가며 그 크기가 매우 크다. 이러한 단어들을 학습시키기 위해Hidden layer를 쌓게 된다. (WordwVec에서는 보통 확률 Vector로 변환시킨다. 그리고 이를 위해 softmax 함수가 활용되어 최종 결과를 내보내게 된다.)

만약 주어진 단어의 corpous가 500만개 그리고 hidden layer가 5000이라면 500만 x 5000의 W와 W gradient가 나타나게 된다.

이렇게 나타난 결과와 실제값인 one-hot vector와의 오차를 구하고 모든 단어에 대해 embeding update를 진행하게 된다.

Input vector는 one hot encoding된 vector로 1수자만 1이고 나머지는 0이다. forward에서는 따라서 큰 문제가 없으나 backpropagation을 하게 되면 너무나 많은 쓸모없는 연산을 진행해야 한다. 예를 들어, 강아지에 대한 결과값의 update에 창문, 노트북 이런 것들도 영향을 미치게 되는 것이다. 따라서 계산의 효율성을 높이기 위해 negative sampling 방식을 사용한다.

negative sampling은 parameter를 update 시킬 negative sample 몇 개를 일부만 뽑아서 그것에 해당하는 parameter를 업데이트시키는 것이다. 기본적으로 영향도가 높은 단어들은 선택이 되고 negative sample 일부가 무작위로 선택되는 것이다. 그리고 영향도가 높은 sample에 대해서는 positive를 부여 그렇지 않은 단어에 대해서는 negative를 부여해 이진 분류 문제로 변환해 학습시키는 방식이다.

주변부 단어로 선택되는 것은 빈번하게 등장하는 단어들이기 때문에 빈번하게 출연하는 단어들에 대한 학습에 유리하다. 즉, 전체 corpus중 문장에 사용되는 비중이 높은 단어를 우선적으로 가중치를 줘서 선별한다.

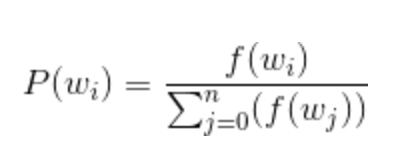
해당 확률은 i번째 단어에 대해 $f(w_i)$는 단어의 빈도 = 출연횟수 / 전체 corpous 수이다.

보통 여기에 3/4제곱을 취해준 공식으로 선택하는 경우가 많다(그러면 성능이 더 좋아진다고 함)

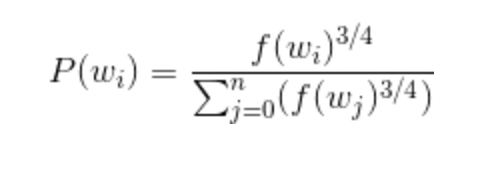
💡 Hierarchical Softmax

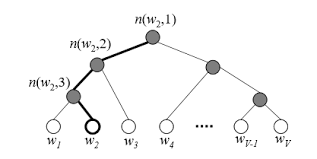
Hierarchical Softmax 역시 negative sampling과 마찬가지로 연산이 너무 비대해지는 것을 막기 위해 고안된 방식이다. Hierarchical Softmax의 특징은 softmax를 통해 확률을 구하고자 할 때 분모로 모두 더하는 방식이다. HHierarchical Softmax는 이를 무시하고 확률을 구하고자 한다. 모델 구조 자체를 full binary tree 구조로 바꾼 후에 단어들은 leaf node에 배치되게 된다.

leaf node까지 가기 위해 거쳐가는 노드들은 벡터가 존재하며 이들을 학습시키는 것이 우리의 목적이다. 즉, 내가 w4라는 단어의 주변부 단어가 w2라는 단어일 때 이 둘에 대한 확률값을 만들어야 한다. 각 leaf node까지 가는데 만나는 node에 해당하는 vector들을 내적해주고 sigmoid 함수 $\sigma$를 통해서 확률값으로 만들어준 후 이들을 곱해나가며 leaf node까지 내려간다. 최종적으로 나타나는 확률값을 최대화 혹은 최소화(positive인지 negative인지에 따라)시켜주는 학습을 통해 결과적으로 parameter를 업데이트 시켜주는 것이다.

결과적으로 우리는 sigmoid 함수만 이용해 softmax를 사용하지 않아도 되는 편리함을 얻게 된다.

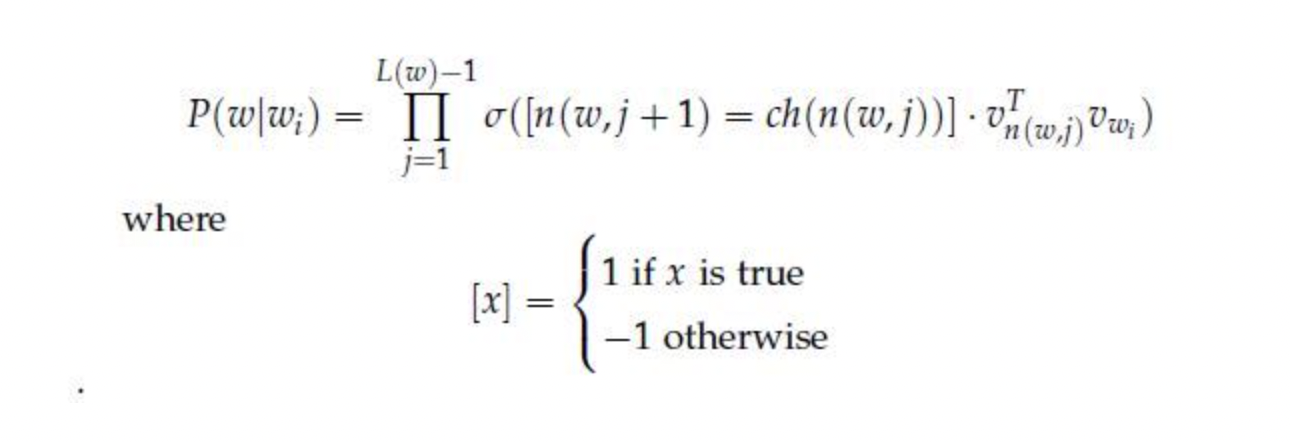
위의 수식은 root로부터 내려갈 때에 이전 노드로부터 좌측으로 이동하면 1을 우측으로 이동하면 -1을 선택하라는 수식이다. sigmoid 함수 특성상 $\sigma(x)+\sigma(-x) = 1$이다. 이렇게 선택하면 수식은 아래와 같아지고 각각의 확률을 구할 수 있다.

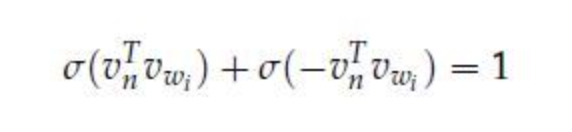
따라서 i번째 vector는 학습이 진행됨에 따라 update가 될 것이고 이에 따라 복잡한 연산을 배제할 수 있으며 모든 단어에 대한 학습이 log(V)로 줄어든다는 큰 장점이 있다.

💡 Distributed Representation

기존에 단어들의 표현은 one-hot encoding을 통해 sparse한 vector로 표현하는 것이 대부분이었다. 그러나 이는 단어에 대한 index 역할만 가능할 뿐, 더 나은 성능을 기대하기는 어렵다. 이에 대해서 나타난 것이 Distributed Representation이다.

Distributed Representation는 단어를 각각의 독립적인 차원으로 one-hot encoding시키는 것이 아니라 우리가 정한 차원으로 대상들을 projection시키는 것이다.

그렇게 나타난 vector는 sparse하지 않고 모든 차원이 값을 가지고 있는 벡터로 표현이 된다. Distributed라는 것도 단어의 특성이 Latent Vector처럼 여러 차원에 분포되어있기 때문이다.

이러한 Distributed Representation은 단어를 여러 차원으로 표현된 속성들로 대표할 수 있고 이는 더 나아가 단어들간의 연관성을 만들어줄 수 있는 길목이 된다.

💡 n-gram

n-gram은 n개의 연속적인 단어 나열을 의미한다. 즉, 갖고 있는 코퍼스에서 n개의 단어 뭉치 단위로 끊은 것을 하나의 토큰으로 간주한다.

📌 "An adorable little boy is spreading smiles"라는 문장이 있을 때, 각 n에 대해서 n-gram을 전부 구해보면 다음과 같다.

unigrams : an, adorable, little, boy, is, spreading, smiles
bigrams : an adorable, adorable little, little boy, boy is, is spreading, spreading smiles
trigrams : an adorable little, adorable little boy, little boy is, boy is spreading, is spreading smiles
4-grams : an adorable little boy, adorable little boy is, little boy is spreading, boy is spreading smiles

n이 1일 때는 유니그램(unigram), 2일 때는 바이그램(bigram), 3일 때는 트라이그램(trigram)이라고 명명하고 n이 4 이상일 때는 gram 앞에 그대로 숫자를 붙여서 명명한다.

보통 이렇게 나누어진 n-gram을 반복적으로 학습시키며 단어와 단어간의 연관성을 유추하게 된다. 과거에는 상당히 많이 사용되었으나 현재는 잘 쓰이지 않는 것으로 알고 있다.

참고 : https://wikidocs.net/69141
https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/03/30/word2vec/
https://ddiri01.tistory.com/310
https://velog.io/@numver_se/Efficient-Estimation-of-Word-Representations-in-Vector-Space