얼마전에 인턴으로 입사하게 된 회사에서 가장 처음 맡게 된 업무는 불균형한 데이터와 multi label을 위한 focal loss 제작 업무였다. 이를 위해 발표 자료를 정리하는 겸 해당 내용에 대해 정리를 해보았다.
생각보다 잘 이해하고 있다고 생각했지만 늘 그렇듯,,, 아니었다..
1) Focal Loss란?
(1) Cross Entropy, Balanced Cross Entropy 개요
Focal Loss를 한 마디로 정리하면 Cross Entropy의 클래스 불균형 문제를 다루기 위한 개선된 버전이라고 볼 수 있다. 즉, 어렵거나 쉽게 오분류되는 케이스에 대하여 더 큰 가중치를 주는 방법을 구현한 것이다. 반대로 쉬운 케이스의 경우 낮은 가중치를 반영한다.
Focal Loss가 등장하고 처음 사용된 곳은 Object Detection으로 이미지의 특성상 모델이 찾아야 하는 객체보다 배경이 많기 때문에 이를 보완하고자 Focal Loss라는 개념이 등장했다.
클래스 불균형 문제는 다음 2가지 문제의 원인이 된다.
① 대부분의 Location은 학습에 기여하지 않는 easy negative(하늘, 산 등)이므로 학습에 비효율적이다.
② easy negative 각각은 높은 확률로 객체가 아니기에 loss 값은 작다. 하지만 비율이 굉장히 크므로 전체 loss 및 gradient를 계산할 때, easy negative의 영향이 압도적으로 커지는 문제가 발생한다
기존 Cross Entropy Loss는 아래와 같다
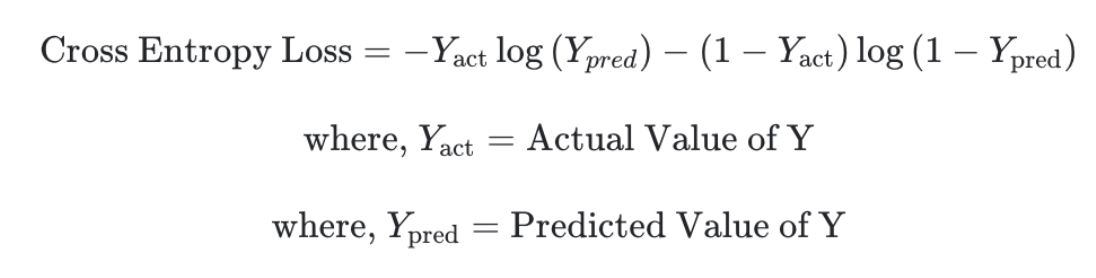
이를 Y=1인 케이스에 대해 표기하면 아래와 같다.
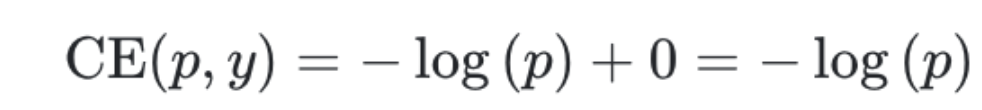
- 만약 p 의 값이 1이면 CE(p,y)=0 이 된다. 즉, 잘 예측하였지만 보상은 없으며 단지, 페널티가 없어진다.
- 반면 p 의 값을 0에 가깝게 예측하게 되면 CE(p,y)≈∞ 가 됩니다. 즉, 페널티가 굉장히 커지게 된다.
여기서 Focal loss는 의 term을 추가한다. 기본적인 Cross Entropy는 γ가 0일 때 이다.
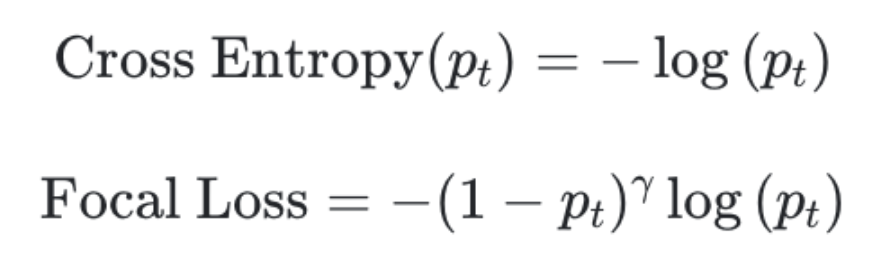
- 여기서 추가된 (1−pt)γ 의 역할은 easy sample에 사용되는 loss의 가중치를 줄이기 위함이다
- 예시를 통해 표현하면 하나의 이미지를 patch로 나누었다고 가정하고
첫번째 patch는 Object가 존재하는 케이스이며 이 때, Y=1 이라고 하며 p=0.95 라고 가정하자.
두번째 patch는 Background에 대한 케이스이며 이 때, Y=0 이라고 하며 p=0.05 라고 가정하자.
그렇게 되면 loss는 아래와 같이 동일하게 나타난다.
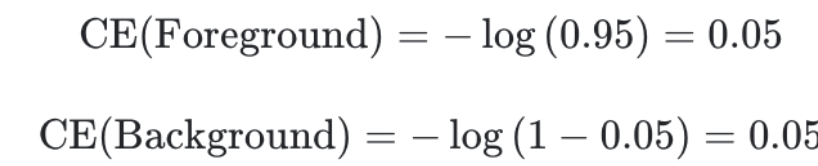
하지만 그렇게 되면 문제점은 Foregound 케이스와 Background 케이스 모두 같은 Loss 값을 가진다는 것에 있다. 왜냐하면 Background 케이스의 수가 훨씬 더 많기 때문에 같은 비율로 Loss 값이 업데이트되면 Background에 대하여 학습이 훨씬 많이 될 것이고 이 작업이 계속 누적되면 Foreground에 대한 학습량이 현저히 줄어들기 때문이다.
이를 가장 쉽게 보완할 수 있는 방안은 우리가 더 학습시키고 싶은 loss에 대해 weight를 주는 것이다. 각 클래스의 loss 비율을 조절하는 weight 를 곱해주어 imbalance class 문제에 대한 개선을 하고자 하는 방법이 Balanced Cross Entropy Loss이다.
이것의 문제점은 Easy/Hard example 구분을 할 수 없다는 점입니다. 단순히 갯수가 많다고 Easy라고 판단하거나 Hard라고 판단하는 것에는 오차가 발생할 수 있습니다.
(2) Focal loss 개요
Focal loss는 Easy Example의 weight를 줄이고 Hard Negative Example에 대한 학습에 초점을 맞추는 Cross Entropy Loss 함수의 확장판이라 볼 수 있다.
Cross Entropy Loss 대비 Loss에 곱해지는 항인 에서 γ 의 값을 잘 조절해야 좋은 성능을 얻을 수 있다.
추가적으로 전체적인 Loss 값을 조절하는 α 값 또한 논문에서 사용되어 α,γ 값을 조절하여 어떤 값이 좋은 성능을 가졌는 지 보여주었다.
- Binary Cross Entropy의 경우 Foreground의 경우 0.75가 적용되면 Background는 0.25가 적용되는 식으로 전체적인 loss를 결정해줄 수 있다.
식은 아래와 같으며 논문에서는 α=0.25, γ=2 를 최종적으로 사용했다.
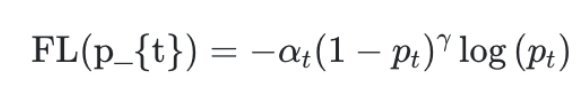
위의 수식을 그래프로 나타내면 아래와 같다.
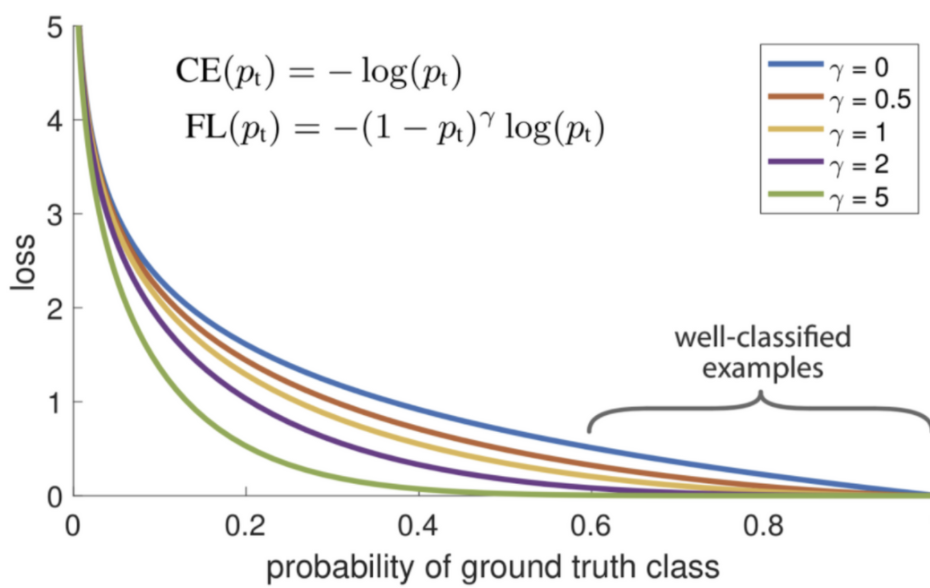
γ 값이 올라갈 수록 loss값이 전체적으로 감소하게 된다. 그러나 비율적으로 살펴보았을 때 γ이 상승할 수록 잘 맞추지 못하고 있는 대상들에 대해 더 압도적인 loss가 적용되게 된다. 이를 focusing parameter 라고 하며 Easy Example에 대한 Loss의 비중을 낮추는 역할을 합니다.
그리고 여기서 너무 거대해지는 것을 막아주기 이해 보통 alpha 값을 통해 보정해준다고 생각하면 된다.
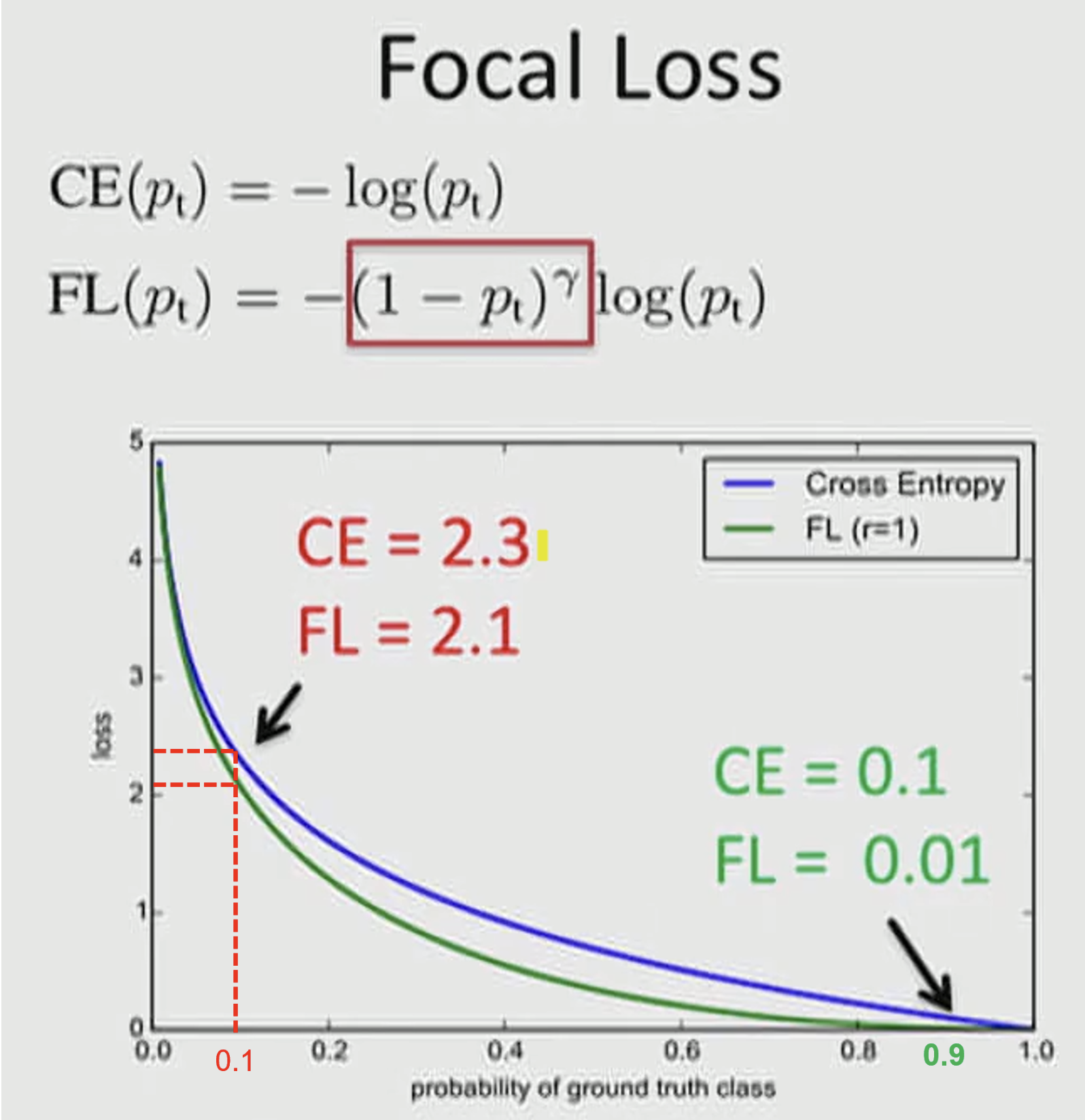
① 빨간색 케이스의 경우 Hard 케이스의 문제이며 ② 초록색의 경우 Easy 케이스의 문제입니다. 그래프에 적용된 α=1,γ=1 입니다.
- ①에서는 pt=0.1 이므로 CE(0.1) = − log(0.1) = 2.30259... ≈ = 2.3이고 FL(0.1) = − (1−0.1)log(0.1) = 2.07233... ≈= 2.1 이다.
- ②에서는 pt=0.9 이므로 CE(0.9)=−log(0.9)=0.105361...≈=0.1 이고 FL(0.9) = − (1−0.9)log(0.9) = 0.0105361... ≈= 0.01 이다.
- 즉, 비율적으로 살펴볼 때 압도적인 차이가 생긴다
- Hard 케이스 보다 Easy 케이스의 경우 weight가 더 많이 떨어짐을 통하여 기존에 문제가 되었던 수많은 Easy Negative 케이스에 의한 Loss가 누적되는 문제를 개선한다.
(3) Class-Balanced Loss 개요
class-balanced loss는 focal loss를 약간 개량한 것으로 long-tailed data set에서 class imbalance 문제를 해결하기 위해 제안되었다. long-tailed data set은 몇 개의 클래스가 데이터의 대부분을 차지하고, 나머지 클래스가 차지하는 양은 적은 데이터셋을 의미한다.
이 경우 기존의 해결 방법은 re-sampling 및 re-weighting 같은 re-balancing 방법을 사용하는 것이지만 크게 효과적이기는 어렵다고 말한다. 해당 논문에서는 samples수가 증가함에 따라 새롭게 추가되는 정보의 양은 줄어든 다는 점에 집중하여 문제를 해결하려 하며, 이를 위해 각 데이터가 점이 아닌 영역으로 연관지어 데이터가 overlab 되는 정도를 측정합니다.
데이터가 적은 class에 해당하는 데이터가 추가되면 새롭게 추가되는 정보는 많을 것입니다. 각 데이터가 영역을 갖고 있다고 가정할 시에 다른 데이터와 overlab 될 확률이 적기 때문입니다. 반대로 데이터가 많은 class에 해당하는 데이터가 추가되면 해당 데이터는 다른 데이터와 overlab 될 확률이 많습니다. 이는 새로운 데이터가 새로운 정보를 거의 포함하고 있지 않다는 것을 의미합니다.
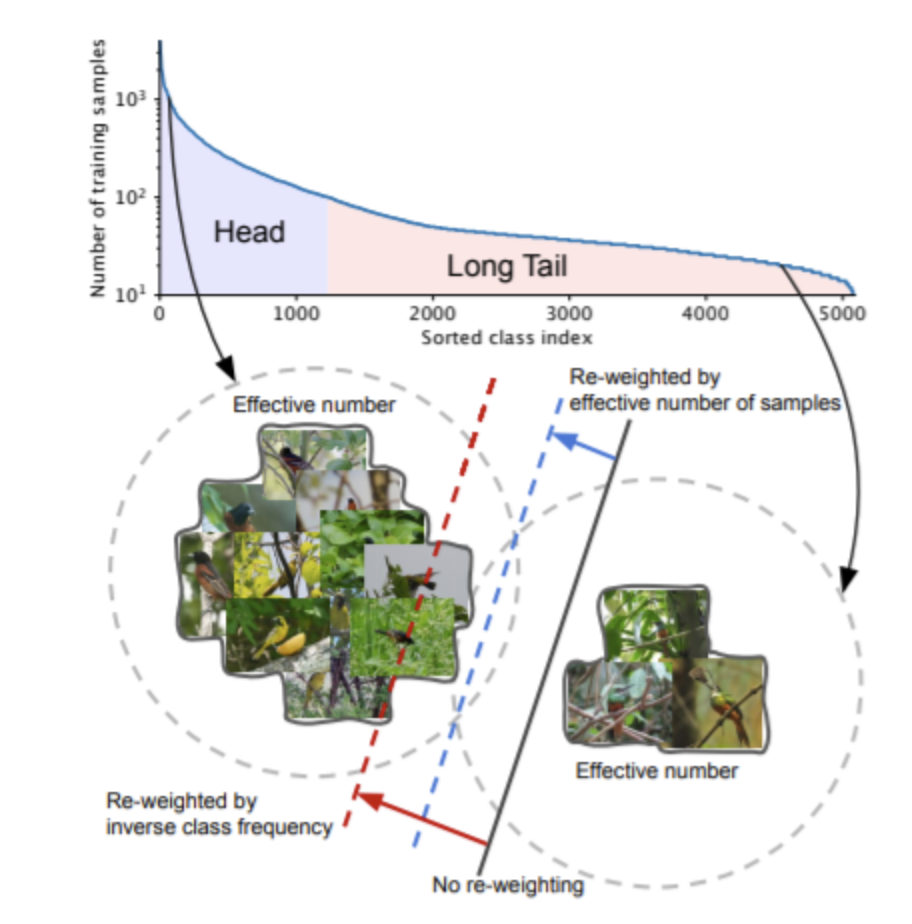
long tailed dataset은 위그림 처럼 적은 수의 클래스가 데이터의 대부분을 차지하고, 나머지 클래스가 데이터의 소수를 차지하고 있는 경우를 의미한다. 이경우에 일반적으로 re-sampling과 cost-sensitive re-weighting 방법을 사용할 수 있다.
(1) re-sampling 방법
re-sampling 방법은 over-sampling 방법과 under-sampling 방법이 있다. 하지만 두 가지 모두 효과적이지는 못하다.
보통 over-sampling보다 under-sampling이 더 선호되지만 중요한 정보를 담고 있는 샘플을 버리는 위험이 발생하는 등 여러 단점이 존재한다.
(2) Cost-Sensitive re-weighting
cost-sensitive re-weighiting 방법은 주어진 데이터 분포를 맞추기 위해서 샘플에 가중치를 부가하는 것이다. 주로 inverse class frequency 또는 smoothed version of inverse square root of class frequency 방법을 사용한다.
- 쉽게 말하면 자주 등장하는 class에 대해서 그 빈도수의 역수를 곱해주어 loss 반영이 적게 되도록 설정하는 것
또다른 방법은 RetinaNet이 사용하는 focal loss 방법입니다. focal loss는 hard example에 대하여 높은 가중치를 부여하고, easy sample에 대하여 낮은 가중치를 부여한다. 또한 minor class에 높은 가중치, major class에 낮은 가중치를 부여할 수도 있습니다.
하지만 이런 방법은 샘플의 수와 샘플의 난이도 사이에 직접적인 연관이 존재하지 않기에 데이터 class의 숫자에 대한 고려가 적다는 단점이 있다.
이를 보완하고자 effective number of samples라는 방식이 등장했다.
Effective Number of Samples
해당 논문에서는 random covering의 단소화된 버전으로서 data sampling 과정을 공식화한다. 핵심 아이디어는 각 샘플이 한 점이 아니라 작은 근접 영역으로 연관짓는 것이다.
모든 데이터 수가 N이고 공간 S에 속해있다고 하겠습니다. 하나의 샘플의 영역 크기는 1입니다. 공간 S를 채우기 위해서는 무수히 많은 샘플을 뽑아야 하며, 각 샘플은 영역을 갖고 있으므로 샘플이 overlab 될 수 있습니다. overlab 되는 경우에 유의미한 정보를 갖고 있지 않다고 간주하며 그렇지 않을 때의 정보에 대해서 집중하고자 하는 것이다.
overlab을 어떻게 판단할까요? 논문에서는 확률을 사용합니다. p확률로 overlab되고, (1-p)확률로 overlab 되지 않습니다. p는 다음과 같이 정의한다.
은 effective number이며 데이터의 평균 부피를 의미한다. 즉, 은 이전 데이터가 공간 S에서 차지하고 있는 부피를 의미하며, 이 값이 커질수록 overlab할 확률이 높아진다.
effective number는 다음과 같이 정의됩니다.
해당 수치에 대한 증명은 아래와 같다.
일단 우리에게 sample이 하나만 있을 때에 일 것이다. 그리고 위의 확률로 overlab이 된다고 할 때에 에 대한 식은 아래**와 같다.
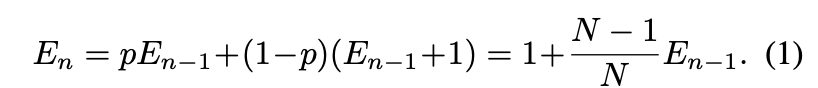
여기서 라고 가정하고 식을 정리하면,
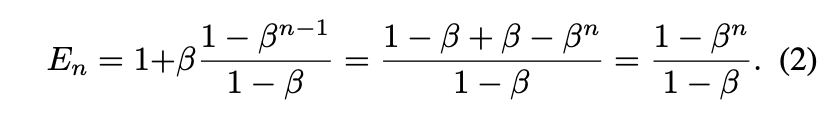
예쁘게 정리가 된다. 이를 데이터가 n개가 있을 때의 해당 공간을 차지하는 비율로 두고 effective number로 파악하는 것이다.
이와 함께 다르게 증명한 공식도 있다.
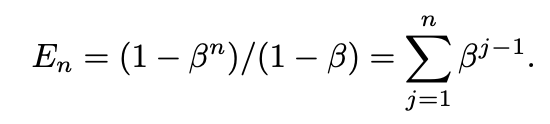
등비수열의 합이라고 생각하면 편하다. 여기서 n을 무한대로 보내게 되면 결과값은 가 될 것이고 결과적으로 N이 된다.
이에 대한 증명은 아래와 같다.
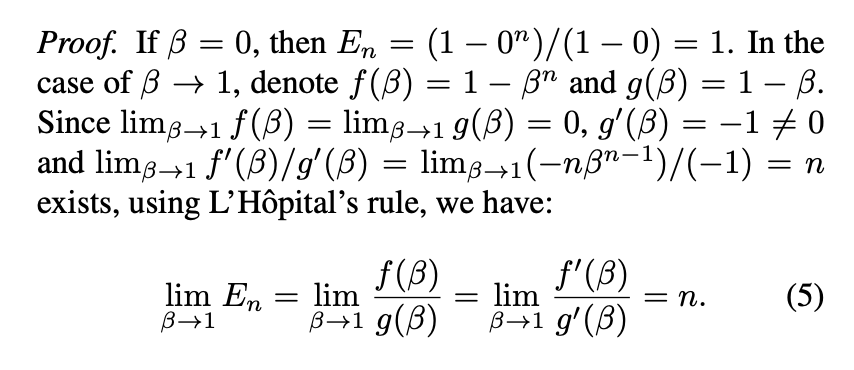
여기서 f(x)는 그리고 g(x)는 로 보면 된다.
베타는 [0,1) 사이에 속하는 하이퍼 파라미터 이며, n이 증가함에 따른 effective number의 증가 속도를 조절합니다. n은 number of samples이다. 이들을 통해 각 loss에 적용할 effective number을 생성해내는 것이다.
Class-Balanced Loss는 softmax cross-entropy, sigmoid cross-entropy, focal loss에 effective number의 역수를 곱한 것이다.
- n이 증가함에 따라 effective number 값은 증가하게 된다.
- n이 적은 클래스에 높은 가중치를 가하고, n이 큰 클래스에 낮은 가중치를 가하기 위해 역수를 곱한다.

