AlexNet과 ViT 논문을 읽다보면 Inductive Bias라는 것이 자주 등장했다. 해당 개념을 알 것 같으면서도 확실히 설명하는 것이 어려워 직접 정리를 한 번 해보고자 했다. 이 포스트를 작성하며 euisuk-chung님과 BaeMI님의 블로그를 많이 참고했기에 함께 읽으면 좋을 것 같다.
📌 1. 딥러닝에서 Bias란?
기본적인 Variance and Bias Trade-off
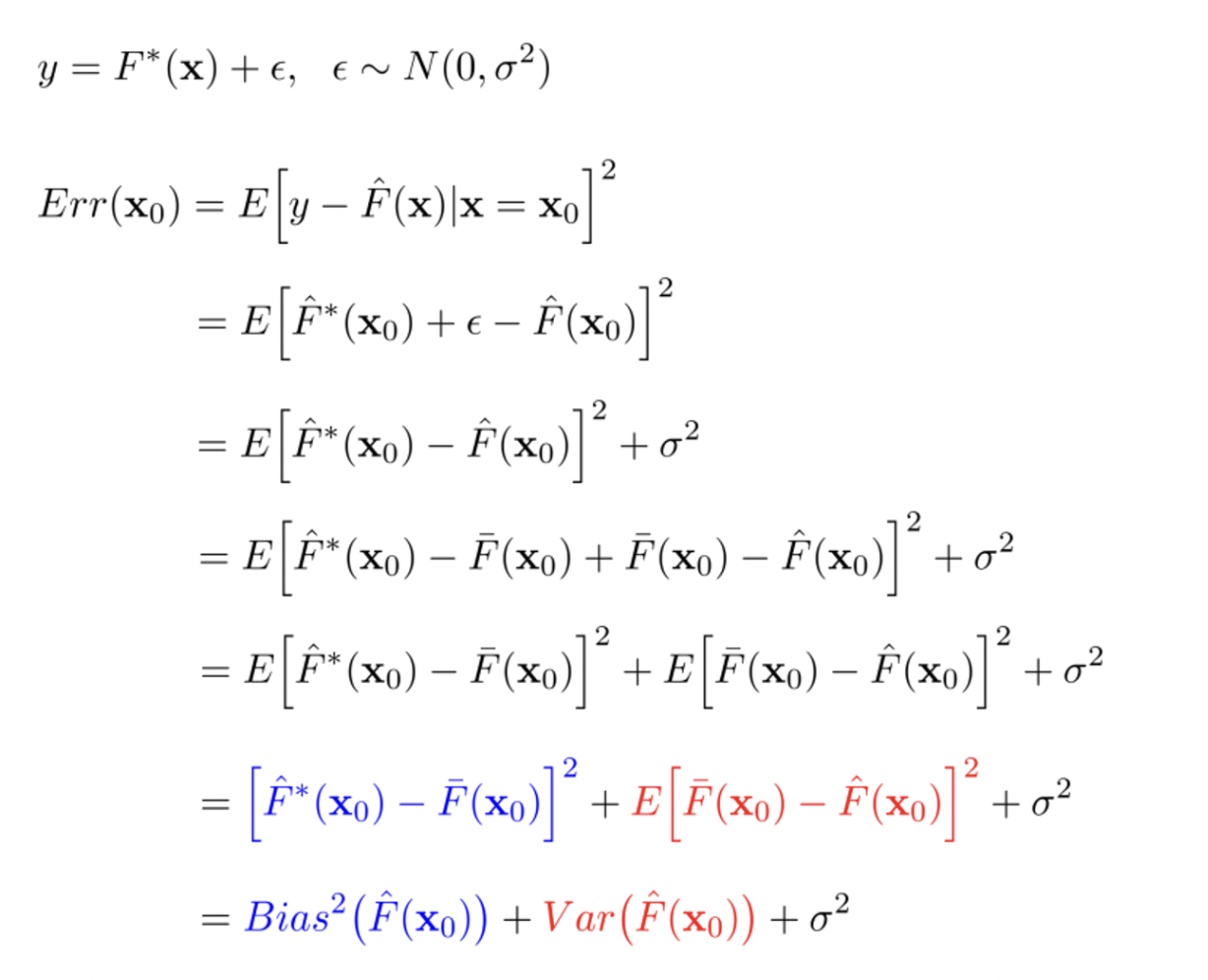
예측을 할 때에 있어 Bias와 Variance는 Trade-off를 가지게 된다.
즉, 두 가지를 모두 취하는 것은 불가능
우리의 집중하는 것에 따라 조절해주어야 할 필요성이 있다.
💡 2. Inductive Bias란?
그렇다면 Inductive Bias란?
일반적으로 모델이 갖는 일반적인 문제점은 모델이 brittle(깨지기 쉽다)하다는 것과, spurious(겉으로만 그럴싸한)하다는 것이 있다.
- Models are brittle : 표본으로 뽑은 분포에 대해서만 모델이 fitting이 된 상태이므로 데이터의 input의 분포가 바뀌면 모델의 결과는 이상해진다.
- Models are spurious : 데이터 본연의 의미를 학습하는 것이 아닌 결과(artifacts)와 편향(biases)를 학습한다.
- 즉, 인과관계를 학습하는 것이 아닌 feature들의 분포를 통해 추론을 끼워맞추고자 하는 것
우리가 모분포로부터 뽑은 표본의 분포가 모분포를 따를 것이라는 보장이 없다. 또한, 표본 분포가 모분포의 예시들을 포괄하지 못하는 경우가 많다.
따라서 우리의 모델이 실제 환경에서 보다 정확한 예측값을 내놓도록 하기 위해 Inductive Bias를 이용하게 된다. Inductive bias란, 학습 시에는 만나보지 않았던 상황에 대하여 정확한 예측을 하기 위해 사용하는 추가적인 가정 (additional assumptions)을 의미한다.
우리의 모델이 훈련 데이터를 넘어 다른 데이터에 대해서도 일반화를 시키는 것을 목표로 한다. 그렇기에 train/valid/test로 데이터를 나누기도 한다. 이 목표로 다가가기 위해 모든 머신러닝 알고리즘에는 내재적인 Inductive Bias가 존재하는데, 이는 모델이 목표 함수를 학습하고 훈련 데이터를 넘어 일반화하기 위해 만든 가정이다.
- 예를 들어 CNN은 해당 pixel은 인접한 pixel들과 깊은 연관을 가지고 있기에 이들을 살펴볼 것이다.
- RNN의 경우 더 짧은 거리를 가지는 sequence 요소들이 지금 시점에 많은 영향을 미칠 것이기에 이들을 통해 결과를 산출할 것이다.
- 위의 특징을 가진 모델들이 학습 과정에서 어떻게 학습되냐에 따라 inductive bias가 생긴다.
즉, inductive bias란 모델이 학습과정에서 본 적이 없는 분포의 데이터를 입력 받았을 때, 해당 데이터에 대한 판단을 내리기 위해서 학습과정 속에서 내재된 속성을 통해 습득된 Bias(편향)이라고 말할 수 있다.
- 즉, input의 어떤 측면을 보아서 biased하게 예측을 할 것인가?
우리가 흔히 말하는 머신러닝/딥러닝을 input과 output의 데이터가 주어지면, 주어진 데이터에 맞는 함수를 가방에서 찾는 것이라고 비유를 할 수 있다.
Inductive Bias는 우리가 함수를 찾는 가방의 크기에 반비례(가정의 강도와는 비례)되는 개념으로 볼 수 있다. 그렇다면 inductive bias는 우리가 input을 통해 예측할 때에 사용할 수 있는 가정들이다.
거의 모든 함수를 표현할 수 있는 MLP의 경우 엄청 큰 가방이고, CNN의 경우 전자보다는 보다 작은 가방으로 보면 된다.
- CNN은 추가적인 가정이 있으므로
🧪 3. Inductive Bias의 종류
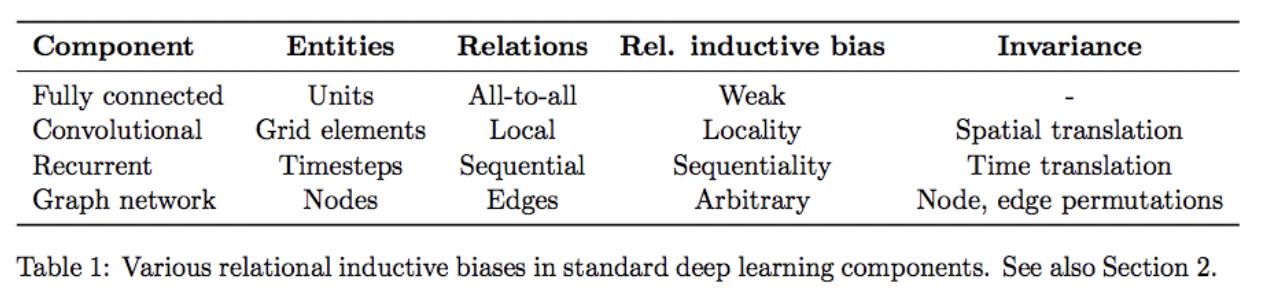
딥러닝에는 아래와 같은 Inductive bias 종류들이 있다. 아래 종류의 Bias들은 알고리즘들이 갖고 있는 고유한 가정 방식이다.
Translation invariance: 어떠한 사물이 들어 있는 이미지를 제공해줄 때 사물의 위치가 바뀌어도 해당 사물을 인식할 수 있어야 한다.Translation Equivariance: 어떠한 사물이 들어 있는 이미지를 제공해줄 때 사물의 위치가 바뀌면 CNN과 같은 연산의 activation 위치 또한 바뀌게 된다. 따라서 Translation invariance를 만족시키기 위해 softmax와 max-pooling 등을 사용한다Maximum conditional independence: 가설이 베이지안 프레임워크에 캐스팅될 수 있다면 조건부 독립성을 극대화하는 것Minimum cross-validation error: 가설 중에서 선택하려고 할 때 교차 검증 오차가 가장 낮은 가설을 선택하는 것Maximum margin: 두 클래스 사이에 경계를 그릴 때 경계 너비를 최대화(SVD)Minimum description length: 가설을 구성할 때 가설의 설명 길이를 최소화하는 것. 이는 더 간단한 가설은 더 사실일 가능성이 높다는 가정을 기반으로 하고 있다.Minimum features: feature가 유용하다는 근거가 없는 한 output에 영향을 미치지 않도록 한다.Nearest neighbors: 대상과 특징 공간에 같이 있는 이웃의 경우 대부분이 동일한 클래스에 속한다고 가정한다.
이처럼 딥러닝 레이어(알고리즘)의 종류에 따라 추가적인 관계 유도 편향을 부과되며 아래는 간단한 예시이다.
CS229 5장에서 앤드류 응 교수님이 GDA(생성 모델)과 Logistic regression(판별 모델)에 대해서 비교하는데 GDA는 Data가 Gaussian Distribution(Exponetial Family)를 따를 것이라는 추가적인 Stronger Assumption이 맞다면 Weaker Assumption(더 적은 가정)인 Logistic regression보다 모델이 문제를 더 잘 풀 수 있다고 말한다.
하지만 Assumption이 틀린 경우(데이터가 푸아송 분포이거나)에는 Logistic보다 동작을 잘 못할 것이다. 즉, 우리가 가정한 것들이 맞다면 보다 잘 예측할 것이고 그러지 못하면 더 적은 가정을 한 모델이 더 잘 예측할 것이라는 뜻이다.
🔬 4. ViT에서는?
이때, ViT 논문에서는 Transformer가 CNN에 비해 inductive bias가 적어 적은 데이터로 더 확실한 예측을 하기 어려워한다고 말한다. 다른 모델에 비해 Transformer는 Positional Embedding이나 Self-Attention 메커니즘을 통해 모든 정보는 활용하지만 추가적인 가정(inductive bias)이 부족하다는 것이다. 왜냐하면 모든 input을 그대로 받아와 attention을 동시에 구해주기 때문이다. 이에 따라 logistic regression처럼 Robust 성질은 높아지지만 정확한 예측을 위해서는 많은 양의 데이터가 필요하다는 것이다.
참고 : https://velog.io/@euisuk-chung/Inductive-Bias%EB%9E%80
https://robot-vision-develop-story.tistory.com/29