[ TIL / 통계 기초부터 다지기] 적률생성함수

💡 중심극한 정리로 나아가기 위한 적률생성함수

중심 극한 정리는 아래와 같다.

모집단의 분포와 상관 없이 표본의 크기 n이 커질수록 표본 평균
$\bar{X}$ 의 분포가 정규분포와 가까워진다.

이를 증명하기 위해서는 먼저 적률생성함수에 대해서 알아야 한다. 이는 아래와 같다.

적률생성함수는 moment generation function(MGF)이라고 불린다. 여기서 적률이란 통계에서 $X^n$에 대한 기대값으로 정의한다.

적률생성함수의 형태는 $Mx(t) = E(e^{tx})$이다. 이를 t로 n번 미분하고 t에 0을 넣게 되면 적률을 도출할 수 있다.

이를 계산하기 위해서 지수함수를 이전에 배웠던 테일러급수 형태로 교체해보자. 그렇게 되면 각 식은 아래와 같아진다.

이를 이용해 적률을 구하는 것은 아래와 같다.

즉, t = 0을 대입하게 되면 나머지 항들은 소거가 되고 해당 횟수의 적률만 남게 된다. 이에 따라 적률생성함수라고 부르게 된다.

그런데 이때 적률생성함수는 확률변수 X의 기대값이 아니라 $e^{tx}$에 대한 기대값을 도출하고 있다. $e^{tx}$는 연속확률변수이기 때문에 적분을 통해 확률을 구해주어야 한다. 이를 통해 도출한 기대값은 아래와 같다.

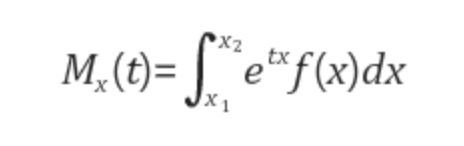
번외) 중심극한정리를 위한 정규분포의 계산은 다음과 같다.

✏️ 한번에 보기

참고) https://www.youtube.com/watch?v=gubleOnA5ys&list=PLmljWRabIwWBxh8V6eIODIz--B802mdLt&index=11