[ TIL / 통계 기초부터 다지기] 중심극한 정리 #1. 두 확률변수의 확률분포가 동일할 조건

💡 중심극한정리와 확률분포

중심극한 정리는 총 3번에 나누어서 정리가 될 것이다. 중심극한정리란 아래와 같다.

모집단의 분포와 상관 없이 표본의 크기 n이 커질수록 표본 평균 $\bar{X}$ 의 분포가 정규분포와 가까워진다.

이를 증명하기 위해서는 가장 먼저 한 가지 선행조건이 필요하다.

두 확률변수의 적률생성함수가 같다면, 둘의 확률분포는 같다.

이를 증명하기 위해 X라는 확률변수와 Y라는 확률변수 그리고 확률분포 f(X), g(Y)를 가정하자.

이들의 적률생성함수는 다음과 같을 것이다. (연속 확률변수이므로 적분을 통해 확률을 도출)

이때, 확률밀도함수값을 무한대로 보내더라도 상관이 없다. 왜냐하면, 정해진 구간 외에서는 확률밀도함수 값이 0이 되기 때문이다. 이를 교체하면 오른쪽과 같아진다.

여기서 한 가지 트릭을 사용한다. X와 Y 확률변수를 모두 포함하는 A라는 집합을 가정한다. 그렇게 되면 각 함수는 a에 대한 수식으로 변경이 가능하다.

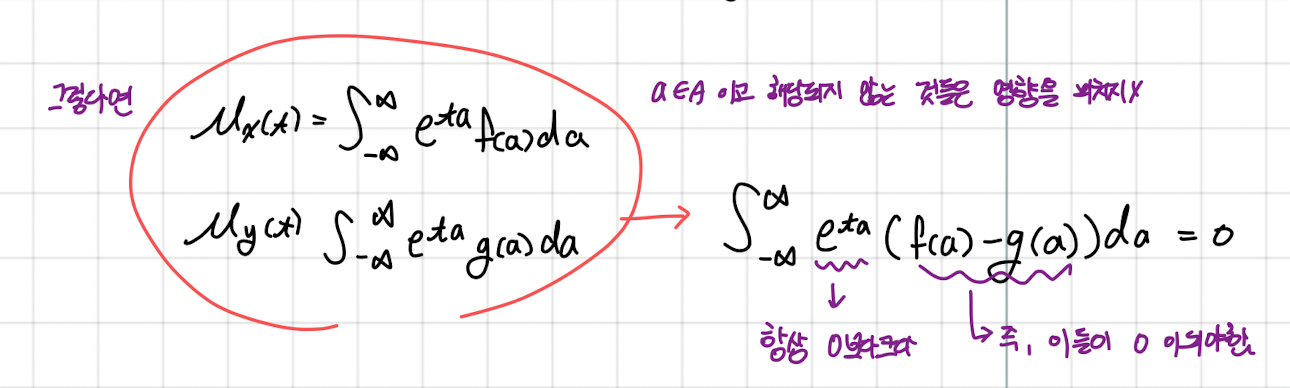
이들의 항을 이항해서 계산하면 오른쪽과 같아진다. 지수함수의 특성상 항상 0보다 큰데 이 값이 0이 나오기 위해서는 f(a)와 g(a)가 같아야 하며 이것이 모든 구간에서 성립해야 한다.

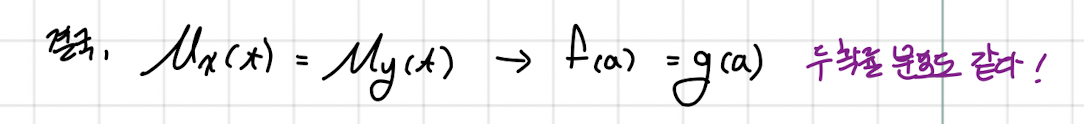
결국 적률생성함수가 동일하면, 두 확률변수의 확률분포가 동일하다는 조건이 성립된다.

✏️ 한번에 보기

참고 : https://hsm-edu.tistory.com/24?category=741767