프리뷰만 몇 편을 작성할지 걱정되는 가운데 두번째로 Postional Encoding과 Residual Connection을 선정했다. Residual의 경우 Resnet 부분을 약간 다루고자 한다.
💡 Positional Encoding
기존의 RNN이 자연어 처리에서 유용했던 이유는 단어의 위치에 따라 단어를 순차적으로 입력받기에 각 단어의 위치 정보(position information)를 자연스럽게 가질 수 있었습니다.
그러나 트랜스포머는 단어 입력을 순차적으로 받는 방식이 아니라 한 번에 모든 단어를 input으로 받아 Encoder에 넣어주기 때문에 단어의 위치 정보를 다른 방식으로 알려줄 필요가 있습니다. 트랜스포머는 단어의 위치 정보를 얻기 위해서 각 단어의 임베딩 벡터에 위치 정보들을 더하여 모델의 입력으로 사용하는데, 이를 포지셔널 인코딩(positional encoding)이라고 합니다.
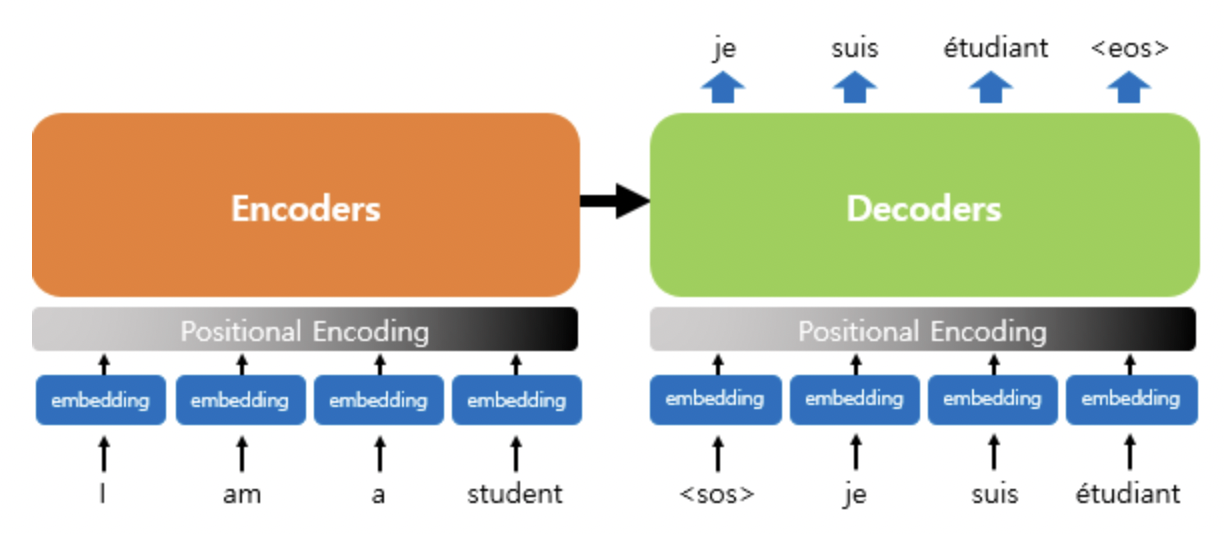
위의 그림에서 볼 수 있듯 입력으로 사용되는 임베딩 벡터들이 트랜스포머의 Encoder와 Decoder에 대한 입력으로 사용되기 전에 포지셔널 인코딩의 값이 벡터에 더해집니다. 이러한 과정을 자세히 보면 아래와 같습니다.
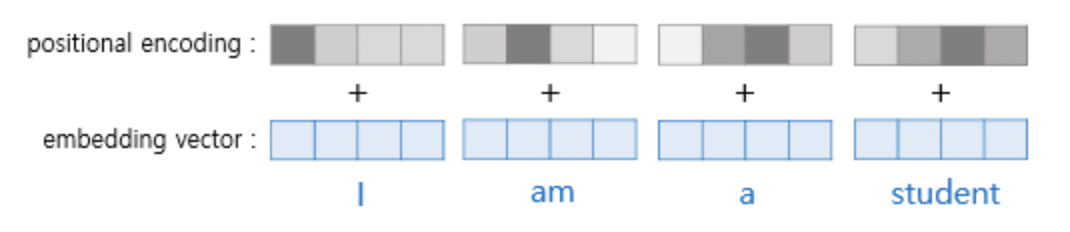
트랜스포머에서는 이러한 postional encoding을 위해 두 개의 함수를 사용했습니다.
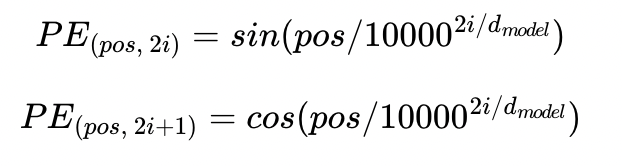
해당 함수는 주기를 가지며 진동하는 sin, cos 함수입니다. 여기서 pos는 우리가 찾고자 하는 단어의 postion, i는 임베딩 벡터 내의 차원의 인덱스를 의미합니다. i가 0부터 까지 증가해가며 각각의 PE 함수값을 구합니다. 이는 결과적으로 Attention의 Energy처럼 사용되어 각각의 단어에 대해 Postion 정보를 줍니다.
여기서 위의 함수는 기존의 sin, cos 함수와 다르며 일종의 학습된 함수가 아닌 기존에 존재하는 함수입니다. 이는, 주기를 가지고 position에 대해서 상대적인 위치의 값을 알 수 있도록 즉, 주기성을 학습할 수 있도록 하는 함수이기만 하면 상관이 없습니다.
따라서 논문에서도 이렇게 정해진 함수값을 사용할 수도 있으나, 위치에 대한 Embedding 값을 따로 학습하도록 해서 Network에 추가해줄 수도 있다고 얘기하며 그렇게 진행하는 것과 단순한 함수를 이용하는 것과 성능 차이는 거의 없다고 말합니다.(대신 학습을 위한 시간은 더 소요됩니다)
따라서 Transformer 이후의 논문들도 기존의 sin, cos 함수를 이용하는 것이 아니라 학습이 가능한 Embedding Layer를 사용하기도 합니다.
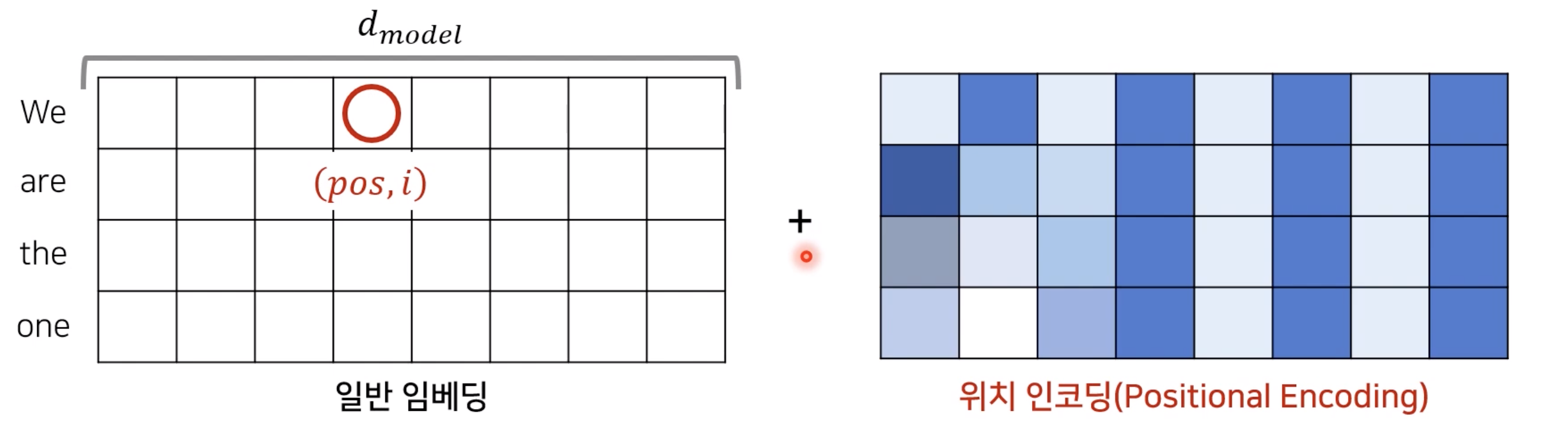
위의 사진처럼 각 Embedding 위치에 대해서 각 pos마다 위치 인코딩을 구해준 후에 그것을 Embedding Vector에 Element wise하게 더해줘서 Postion에 대한 정보를 추가해줍니다.
💡 Residual Connection
Residual Connection은 ResNet에서 등장한 개념입니다. 과거 GoogleNet, VGG 등으로 Deep CNN에 대한 연구가 진행되었으나 깊이가 깊어질 수록 학습이 원할하게 잘 되지 않고 있음을 확인했습니다. 즉, 오히려 shallow한 network 구조가 deep depth를 가지는 모델보다 좋은 성능을 발휘하게 되는 것입니다.
기본적으로 parameter 숫자가 많게 되면 feature space가 복잡해지기 때문에 overfitting이 잘 일어나게 됩니다. 이러한 특성 때문에 Deep CNN 역시 네트워크가 커짐에 따라서 점점 학습이 안 되는 것이었습니다.
이를 해결하고자 한 것이 ResNet입니다.
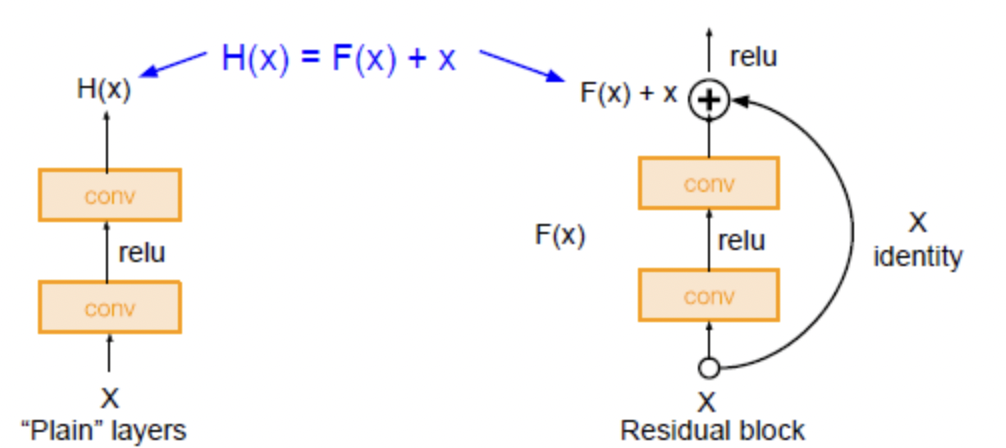
왼쪽은 기존에 사용하던 구조이며 오른쪽은 ResNet에서 사용되는 것입니다. 연산은 동일하게 진행하지만 차이점은 Input X를 Activation Function을 거치기 이전에 더해주느냐 그렇지 않느냐입니다.
기존의 layer는 input X를 넣어주고 function을 통해 나온 Ŷ는 이후의 layer에서 새롭게 학습해야 할 정보입니다. 즉, input X에 대한 내용이 존재하지 않고 오직 Ŷ를 통해서 반복적으로 학습이 일어나게 되는 것입니다. 즉, H(x) = Ŷ가 우리의 target 값인 Y에 가까워지도록 학습을 해야 하는데 이렇게 되면 학습해야 하는 내용이 많아지게 됩니다.
그에 반해 Residual Block의 경우 Ŷ = x + F(x)입니다. 이것이 Activation function을 거치고 논문에서는 이를 Identity function이라고 말합니다
엄밀히 말하면 음수부분이 0이 되기 때문에 Identity function은 아닙니다.
이렇게 나온 Ŷ에 대해서 또다시 Residual을 거치면
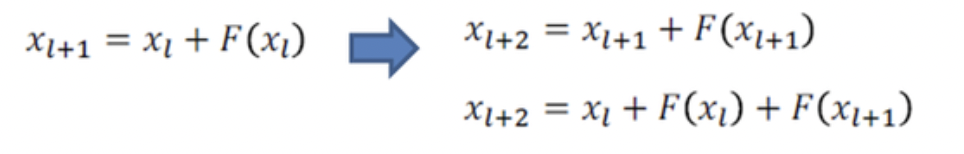
이러한 구조가 반복되게 되며 결과적으로
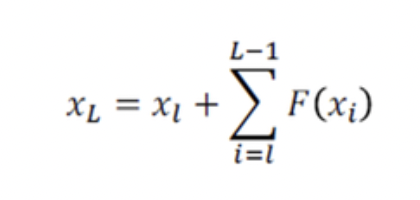
위와 같은 식이 완성되게 됩니다. 즉, 특정 위치의 출력은 특정 위치에서의 입력과 residual 함수의 합으로 표현이 가능해지기 때문에 학습구조가 매우 단순화됩니다.
거기에 더해, output Ŷ가 Y가 되기 위해서는 위의 식이 Y가 되어야 하는데 이는 곧, input x를 제외한 잔차부분만의 학습을 통해서 이루어질 수 있다는 것입니다.
또한, 이러한 최종적 Output과 달리 hidden state로 존재하는 F(x)는 Conv layer입니다. 이러한 Conv layer는 Conv filter를 이미지 혹은 대상에 찍어줌을 통해 feature extraction을 수행하고자 합니다. 결과적으로 나타나는 결과값은 x의 특성을 최대한 잘 보전하기도 하면서 미세한 feature들을 뽑는 것이 목표입니다.
즉, F(x)가 0이 되도록 학습을 진행해주게 되는데(진짜 0이 되지는 못함) x와 함께 갈 약간의 작은 변화만을 갖고 가게 됩니다. 결과적으로 작은 잔차만을 학습하기 때문에 Residual connection이라 말합니다.
참고 : https://www.youtube.com/watch?v=AA621UofTUA&list=PLRx0vPvlEmdADpce8aoBhNnDaaHQN1Typ&index=9
https://ganghee-lee.tistory.com/41
https://itrepo.tistory.com/36
