mean Average Precision이란?
처음 mean Average Precision을 봤을 때, mean과 Precision이 같은 의미 아닌가? 라는 생각이 들었다. 찾아보니, Mean(수학/통계 전문용어)의 경우 어떤 표본의 평균을 표현하는 포괄적 의미의 평균, 뭐 산술평균, 기하평균, 조화평균 등이 이에 해당하고, Average(일반용어)는 여러가지 mean 중 Arithmetic Mean을 의미한다고 한다(더 헷갈리는 느낌이다...).
Object detection task에서 모델을 평가하기 위해 가장 보편적으로 사용되는 평가 지표 중 하나이다. Precision-recall 그래프를 이용해면 특정 알고리즘의 성능을 평가하기에는 좋으나 다른 두 알고리즘을 정량적으로 비교하기에는 어려운 단점이 있다. 이를 해소하고자 Precision-recall 그래프의 아래 면적을 사용하는데 이때, 아래 면적을 구하는 과정에서 평균을 사용한다.
Precision and Recall이란?
이진 분류 기법(binary classification)을 사용하는 패턴 인식과 정보 검색 분야에서, 정밀도는 검색된 결과들 중 관련 있는 것으로 분류된 결과물의 비율이고, 재현율은 관련 있는 것으로 분류된 항목들 중 실제 검색된 항목들의 비율이다. 따라서 정밀도와 재현율 모두 관련도(Relevance)의 측정 기준 및 지식을 토대로 하고 있다[1].
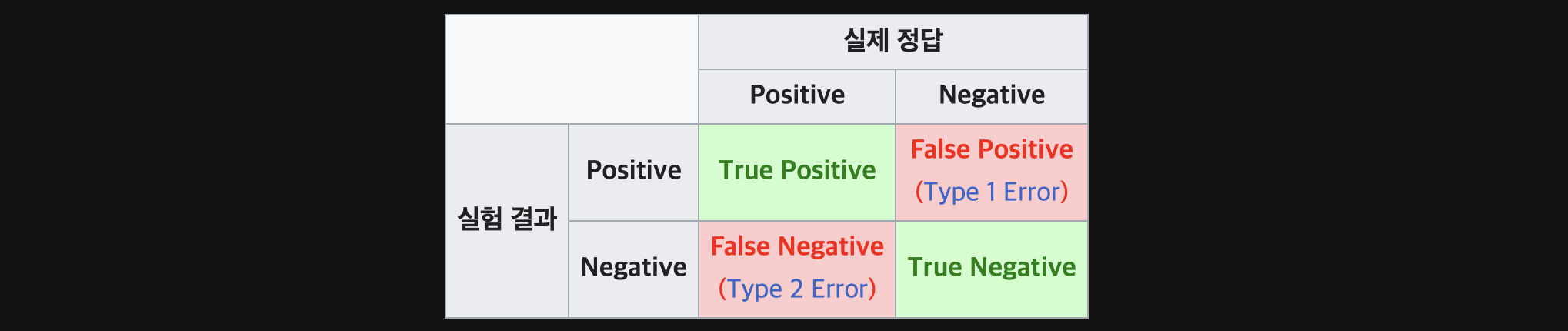
정리하면, [True/False] [Positive/Negative]에서 앞 부분의 True/False는 예측이 맞았는지에 대한 여부이고, 뒤에 Positive/Negative는 예측에 대한 결과라고 볼 수 있다.
- True Positive(TP) : 모델이
Positive로 예측했을 때, 그게 정답(True)인 경우 - True Negative(TN) : 모델이
Negative로 예측했을 때, 그게 정답(True)인 경우 - False Positive(FP) : 모델이
Positive로 예측했을 때, 그게 정답(False)인 경우 - False Negative(FN) : 모델이
Negative로 예측했을 때, 그게 정답(False)인 경우
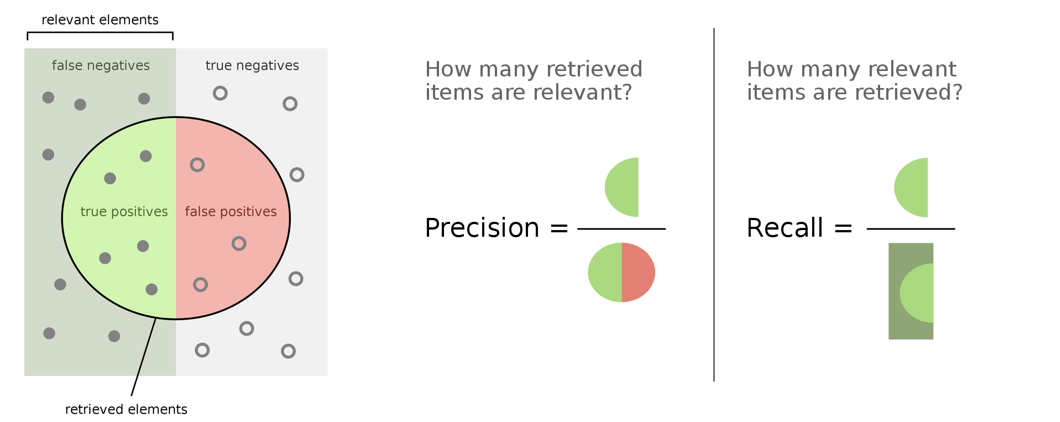
정리해보면, Precision은 모델이 Positive로 분류한 것들 중에 실제로 Positive인 비율을 나타내는 것이고, Recall은 실제 Positive들 중애서 모델이 Positive로 분류한 비율을 의미한다.
이때, 이 두 요소를 가지고 모델을 평가하기 위한 방법으로 Precision-recall Curve가 있다.
Precision-recall Curve란?
Precision-Recall Curve는 모델의 예측 정확도, 즉 실제 Positive를 얼마만큼 잘 찾았는지에 관심을 갖는 그래프를 말한다.
Precisino-recall curve는 다음과 같은 방법으로 그릴 수 있다.

위 그림처럼 3장의 이미지가 있고 강아지만 예측하는 상황이라고 가정한다. 여기서 초록색 박스가 정답이고 빨간색은 모델의 에측 결과이며 숫자는 Confidence score를 의마하고, IoU threshold는 0.5 이상이다. 1번 이지미를 예로들면, 3개의 예측 중 Confidence socre가 0.7인 박스만 IoU threthold 기준에 부합하기 때문에 TP(True Positive)로 분류하고 나머지는 FP(False Positive)로 분류한다.
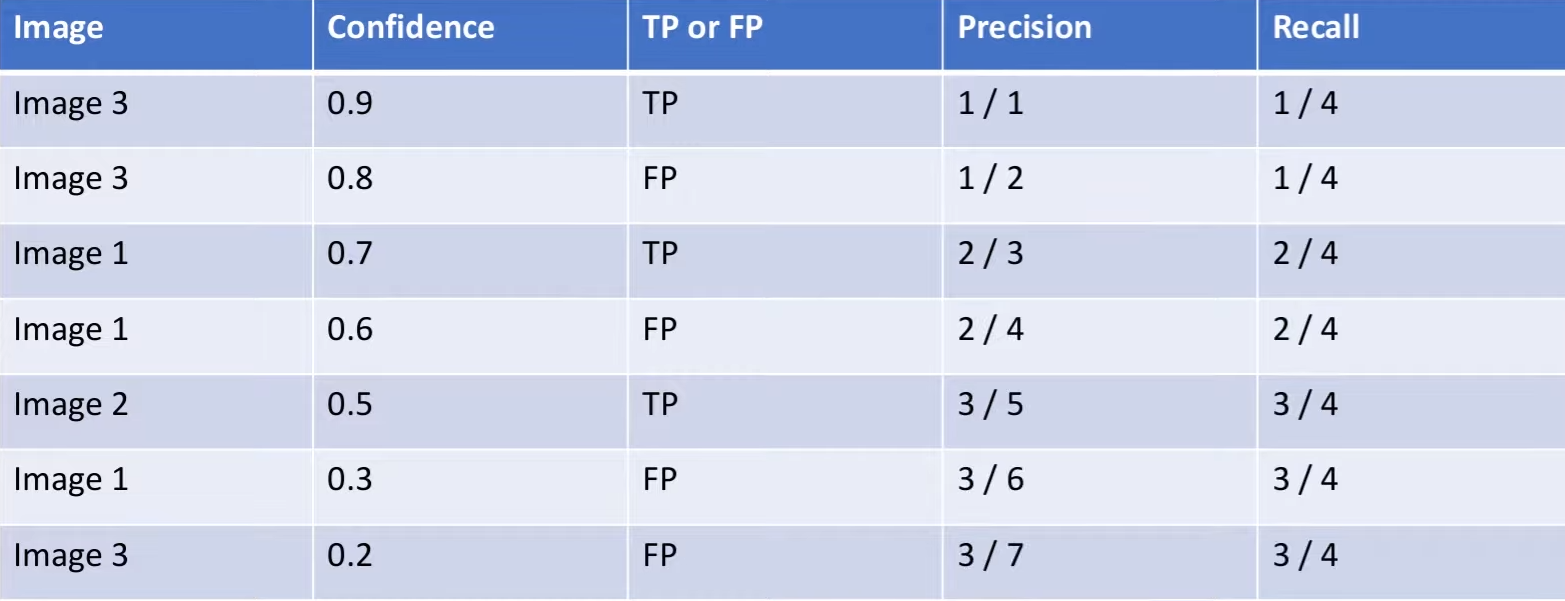
3장의 이미지에 대한 Confidence score와 True인지 False 인지를 기록하면 위 표와같이 정리할 수 있다. Recall의 경우 정답 데이터(초록색 박스)의 개수가 4개이기 때문에 분모가 4, 분자는 TP의 개수를 카운트 하는 형식으로 계산한다. Precision의 경우 모델이 예측한 개수가 분모가 되기 때문에 예측 박수의 개수를 카운트 하는 형식으로 만들어 주면된다.
Average Precision이란?
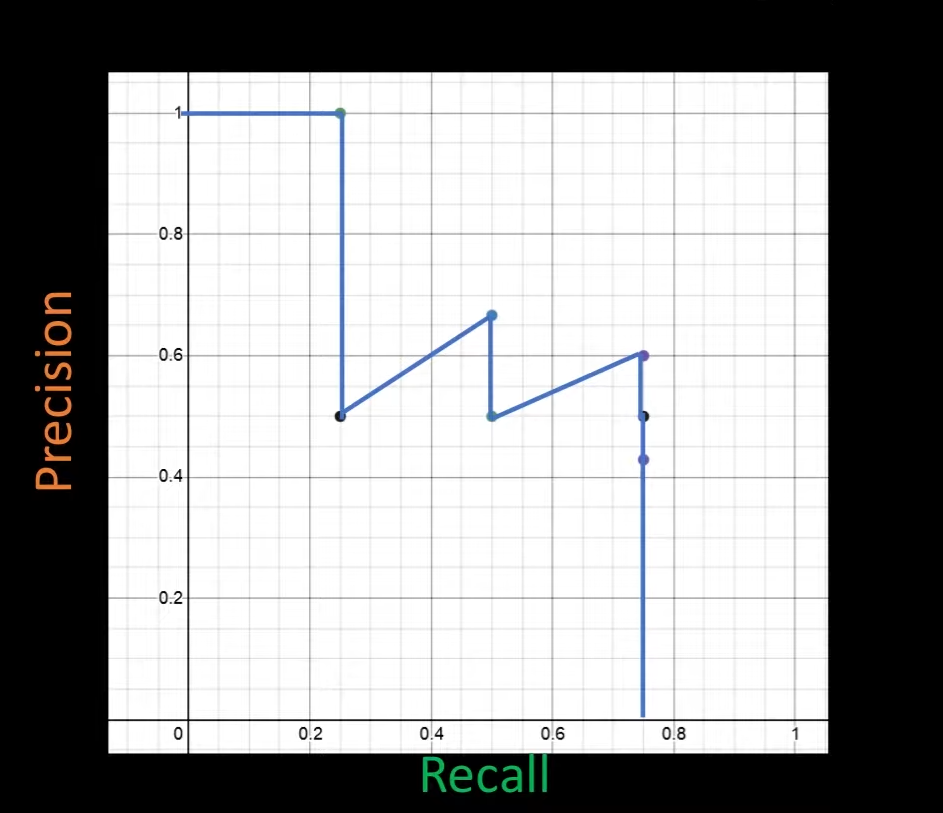
그 다음 x축을 Recall, y축을 Precision으로 그래프를 그리면 Precision-recall curve가 만들어진다. 하지만, P-R curve를 통해 정량적으로 비교하기 위해서 하나의 수로 만들어야 한다. 따라서 curve 밑 면적을 이용한다.
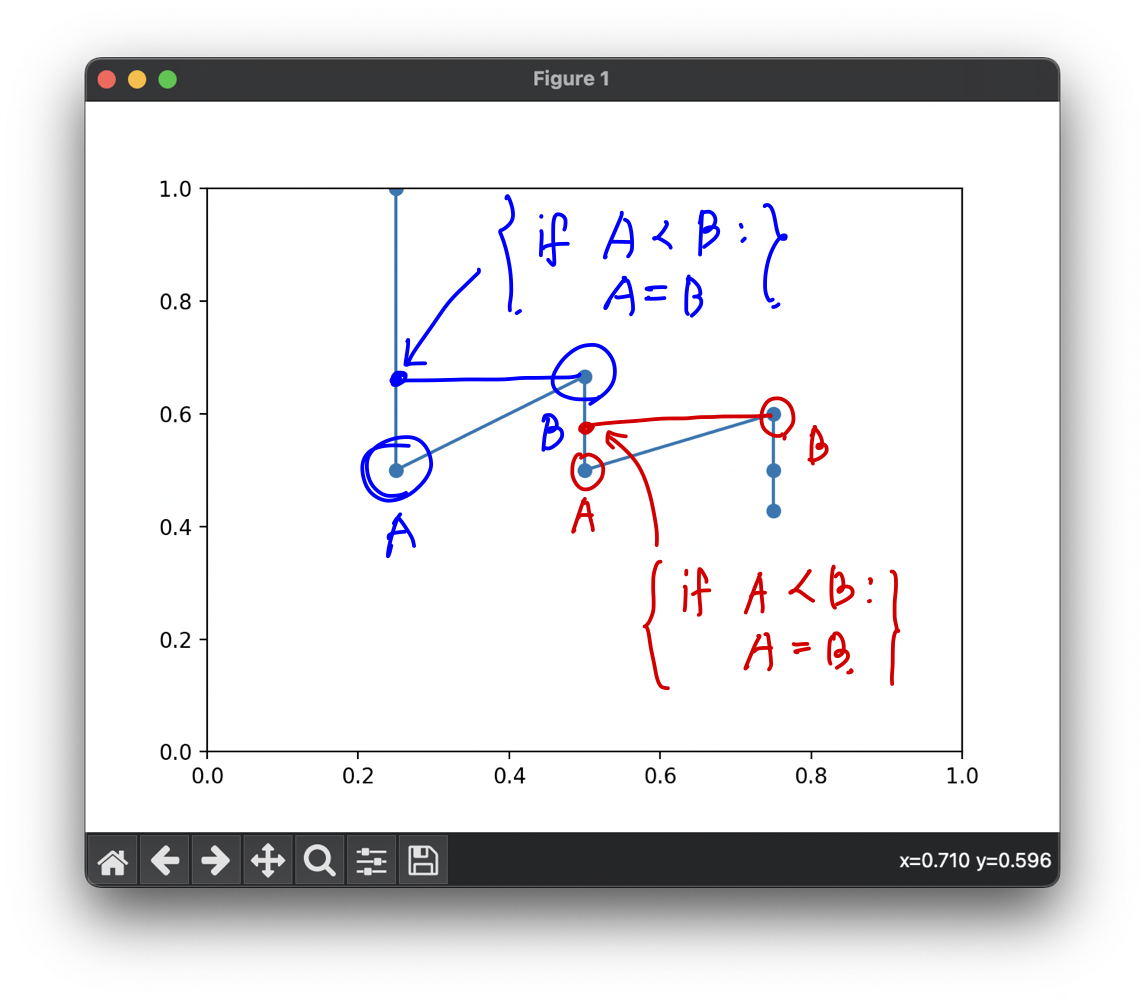
면적 계산을 위해 단조 감소함수 즉, Recall이 커질수록 Precision이 감소하도록 그래프의 경향을 바꿔준다. 이를 interpolation 이라고 한다.
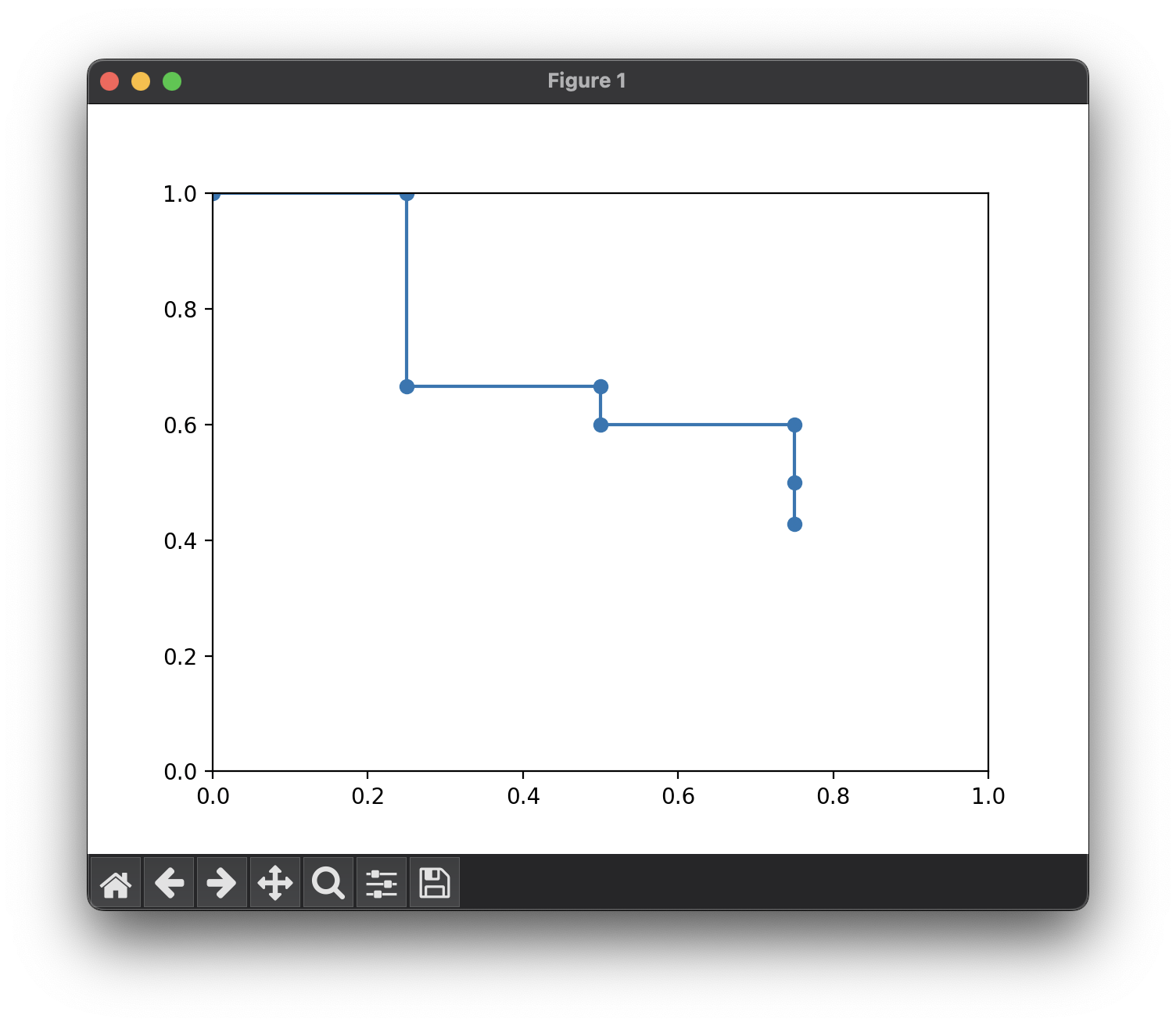
이렇게해서 면적을 구하면, Average Precision을 구한것이다.
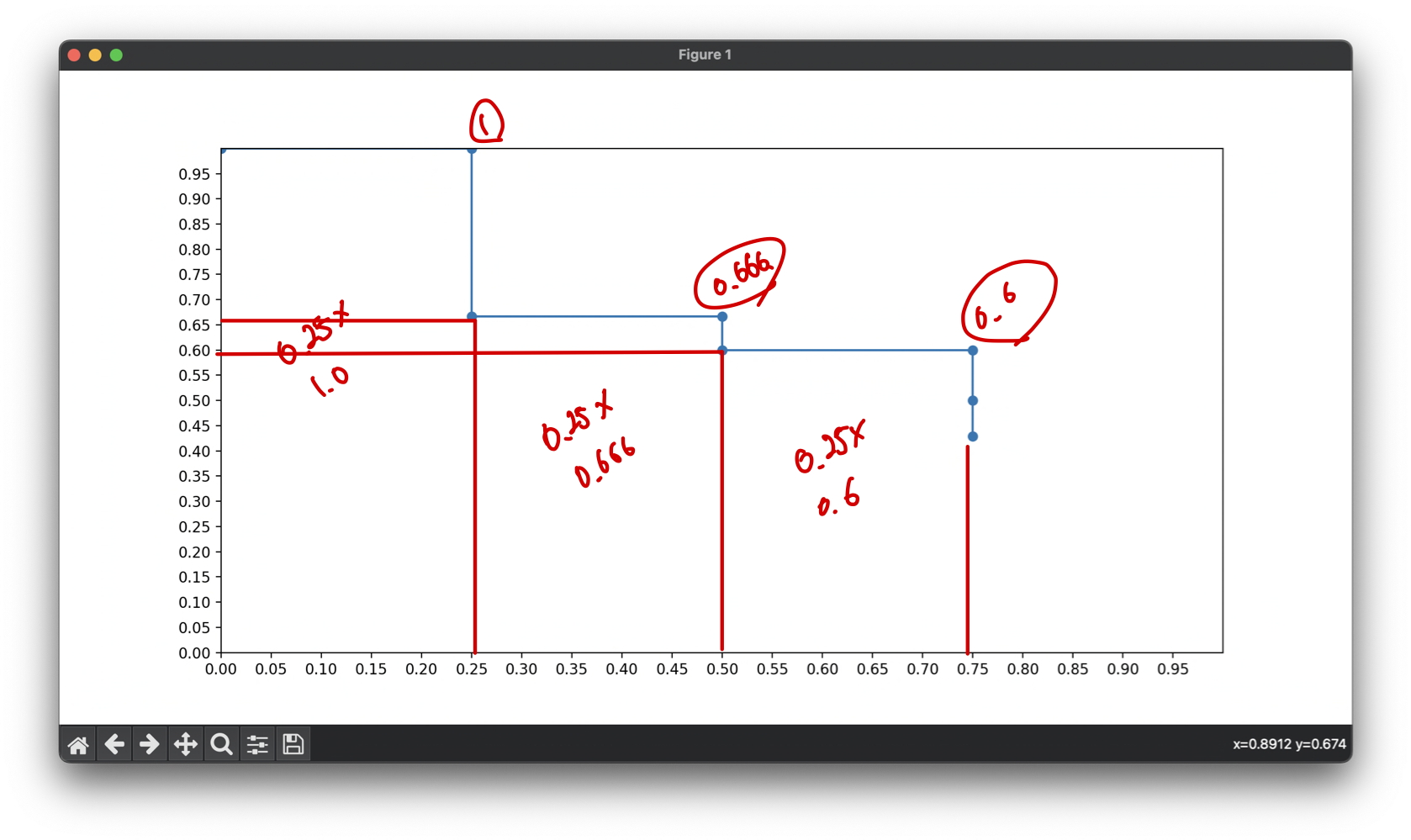
print(0.25 * 1.0 + 0.25 * 0.666 + 0.25 * 0.6) # 0.5665
print(round(np.trapz(precision, recall), 4)) # 0.5667실제로 면적을 구해보면 약 0.57의 값을 얻을 수 있다. 또한 trapz()함수를 이용하면 더 쉽게 면적을 구할 수 있다. 여기까지 하나의 class에 대한 Average Precision을 구했다. 이 과정을 모든 class에 대해서 수행하고 class의 개수로 나눠주면 최종적으로 mean Average Precision을 구할 수 있다.
Implementation with Pytorch
import torch
from collections import Counter
from utils.iou import intersection_over_union
def mean_average_percision(
pred_bboxes,
target_bboxes,
iou_threshold,
num_classes
):
# pred_bboxes = [[img_idx, cls, prob_score, cx, cy, w, h],
# ...]
epsilon=1e-6
average_precisions = []
predictions = []
targets = []
for cls in range(num_classes):
# 동일한 class에 대한 예측 박스와 정답 박스를 저장
for pred_bbox in pred_bboxes:
if pred_bbox[1] == cls:
predictions.append(pred_bbox)
for target_bbox in target_bboxes:
if target_bbox[1] == cls:
targets.append(target_bbox)
# img0 has 3 bboxes
# img1 has 5 bboxes
# num_bbox_per_cls = {0:3, 1:5} 클래스 별 파일의 개수
num_bbox_per_cls = Counter([target[0] for target in targets])
for k, v in num_bbox_per_cls.items():
num_bbox_per_cls[k] = torch.zeros(v)
# num_bbox_per_cls = {0:torch.tensor([0,0,0]), 1:torch.tensor([0,0,0,0,0])}
predictions.sort(key=lambda x: x[2], reverse=True)
# probability로 정렬
TP = torch.zeros((len(predictions)))
FP = torch.zeros((len(predictions)))
num_targets = len(targets)
for prediction_idx, prediction in enumerate(predictions):
target_imgs = [
target_bbox for target_bbox in targets
if (target_bbox[0] == prediction[0])
]
num_targets = len(target_imgs)
best_iou = 0
for target_idx, target_img in enumerate(target_imgs):
iou = intersection_over_union(
torch.tensor(prediction[3:]),
torch.tensor(target_img[3:])
)
if(iou > best_iou):
best_iou = iou
best_target_idx = target_idx
if (best_iou > iou_threshold): # iou_threshold를 기준으로 TP, FP 선정
if num_bbox_per_cls[prediction[0]][best_target_idx] == 0:
TP[prediction_idx] = 1
num_bbox_per_cls[prediction[0]][best_target_idx] = 1
else:
# 이미 처리된 bbox의 경우 FP
FP[prediction_idx] = 1
else:
# iou_threhold를 넘지 못하는 경우
FP[prediction_idx] = 1
TP_cumsum = torch.cumsum(TP, dim=0)
FP_cumsum = torch.cumsum(FP, dim=0)
recalls = TP_cumsum / (num_targets + epsilon)
precisions = torch.divide(TP_cumsum, (TP_cumsum + FP_cumsum + epsilon))
# recall에 따른 precision 그래프를 그릴 때, 0과 1에서 부터 시작하기 위함
precisions = torch.cat(torch.tensor([1]), precisions)
recalls = torch.cat(torch.tensor([0]), recalls)
average_precisions.append(torch.trapz(precisions, recalls))
return sum(average_precisions) / len(average_precisions)