
Optimization (최적화)
최적화를 다들 골짜기에서 밑 바닥을 찾는 과정이라고 비유한다.
내가 있는 곳의 높이가 바로 loss이고, loss는 W에 따라 변하게 되는데 iterative한 방법들을 쓴다. 이는 임의의 지점에서 시작해 점차적으로 성능을 향상시키는 방법이다.
- random search
: 임의로 샘플링한 W들을 엄청 많이 모아놓고 Loss를 계산해서 어떤 W가 좋은지를 살펴보는 것
굉장히 구리고 실제로 사용하면 안되는 것
- 지역적인 기하학적 특성을 이용 (local geometry)
: 두 발로 땅의 경사를 느끼고, 조금 내려가다가 또 어느 방향으로 가야 내려갈 수 있을지를 알아보고 또 내려가고 그러다 끝까지 내려가는 것
→ 그렇다면 경사는 무엇일까?

- 일차원 공간에서 경사는 어떤 함수에 대한 미분값이다.
- 어떤 점에서 경사, 즉 도함수(derivative)를 계산해보면, 작은 스텝, h가 있고 이 스텝 간의 함수 값의 차이를 비교해 본다면 f(x+h) - f(x)
- 그리고 그 스텝사이즈를 0으로 만들면 (h->0) 그것이 바로 어떤 점에서의 이 함수의 경사가 된다.
- 다변수인 상황에서의 미분으로 일반화시켜보면 gradient이고 gradient는 벡터 x의 각 요소를 편도함수들의 집합이다.
- gradient 의 각 요소가 알려주는 것은 바로 "우리가 그쪽으로 갈때 함수 f의 경사가 어떤지" 라는 것
- gradient의 방향은 함수에서 "가장 많이 올라가는 방향"
- gradient의 반대 반향이라면 "가장 많이 내려갈 수 있는 방향"
- 만약에 특정 방향에서 얼마나 가파른지 알고싶으면 그 방향의 유닛벡터와 gradient벡터를 내적
- gradient가 함수의 어떤점에서의 선형 1차근사 함수를 알려주기 때문에 매우 중요.
컴퓨터로 이 gradient를 써먹을 수 있는 가장 단순한 방법 중 하나는 유한 차분법(finite difference methods) 를 이용하는 것

W의 첫번째 요소(0.34) 에 아주 작은 값 h를 더해 보는 것 -> loss를 다시 계산 -> 1.2534에서 1.25322로 감소 -> 극한식을 이용해 FDM으로 근사시킨 gradient를 구함 -> 두번째 요소에도 반복 -> ...
→ 시간이 너무 오래걸림💥, 실제론 이렇게 gradient를 계산하지 않는다!
실제로는 gradient를 나타내는 식을 찾아내 미분해서 찾아냄
-
Numerical gradient : approximate, slow, easy to write => 실제로 사용x
-
Analytic gradient : exact, fast, error-prone
하지만, 작성한 미분 코드가 잘 작동하는지 확인하기 위해 (디버깅 위해) numerical gradient를 사용한다. 유닛 테스트의 일종으로 짠 코드를 확인할 수 있다. 다만 시간이 오래걸리지 않도록 파라미터 스케일은 줄이는 게 좋다.
Gradient Descent

- 우선 W를 임의의 값으로 초기화
- Loss와 gradient를 계산한 뒤에 가중치를 gradient의 반대 방향으로 업데이트 (gradient가 함수에서 증가하는 방향이기 때문에 -gradient를 해야 내려가는 방향. -gradient 방향으로 아주 조금씩 이동할 것이고 이걸 영원히 반복하다 보면 결국에는 수렴할 것)
여기서 스텝 사이즈(-gradient 방향으로 얼마나 나아가야 하는지)는 하이퍼파라피터임.
스텝사이즈는 Learning rate라고도 하며, 실제 학습을 할때 정해줘야하는 가장 중요한 하이퍼파라미터 중 하나이다.
Stochastic Gradient Descent(SGD)

- N이 커지면 gradient descent를 계산하기 굉장히 느려짐.
- 그래서 실제로 쓰는 방법. 전체 데이터 셋의 gradient과 loss를 계산하기 보다는 Minibatch라는 작은 트레이닝 샘플 집합으로 나눠서 학습하는 것.
- Minibatch는 보통 2의 승수로 정하며 32, 64, 128 을 보통 쓴다.
- 이 작은 minibatch를 이용해서 Loss의 전체 합의 "추정치"와 실제 gradient의 "추정치"를 계산하는 것
- SGD는 거의 모든 딥러닝 알고리즘에 사용되는 기본적인 학습 알고리즘이다.
Image feature
Linear classifier는 실제 Raw 이미지 픽셀을 입력으로 받는 방식 -> 좋은 방법이 아님.
딥러닝이 유행하기 전, 주로 쓰이던 두가지 스테이지를 거치는 방법

- 여러가지 feature representation을 계산하는 것
: 여러 특징 표현들은 한데 연결시켜(Concat) 하나의 특징 벡터로 만들어 이 벡터가 Linear classifier의 입력으로 들어가는 것이다.
- 극좌표계를 바꾸어(특징변환) 변환 후 선형 분리가 가능하게 바뀜
이런 기법들은 문제를 풀 수 있도록 하려면 어떤 특징 변환이 필요한가 를 알아내는 것들
- examples
color histogram: 이미지 전체적으로 어떤 색이 있는지
Histogram of Oriented Gradients(HoG) : 이미지 내에 전반적으로 어떤 종류의
edge정보가 있는지, 이미지를 여러 부분으로 지역화해서 지역적으로 어떤 edge가 존재하는지
bag of words: 자연어처리(NLP)에서 문장의 여러 단어의 발생 빈도를 세서 특징 벡터로
사용하는 것을 이미지에 적용한 것으로, 두가지 과정이 있다.

엄청 많은 이미지를 가지고, 그 이미지들은 임의대로 조각낸다.
그리고 그 조각들을 K-means와 같은 알고리즘으로 군집화한다.
이미지내의 다양한 것들을 표현할 수 있는 다양한 군집들을 만들어 내는 것이다.
군집화 단계를 거치고나면, 시각 단어(visual words)는
빨간색, 파랑색, 노랑색과 같은 다양한 색을 포착해낸다. 뿐만 아니라 다양한 종류의
다양한 방향의 oriented edges또한 포착할 수 있다. 이런 시각 단어(visual words) 집합인 Codebook을 만들고 나면 어떤 이미지가 있으면, 이 이미지에서의 시각 단어들의 발생 빈도를 통해서 이미지를 인코딩 할 수 있는 것이다. 그리고 이는 이 이미지가 어떻게 생겼는지에 대한 다양한 정보를 제공한다.
Image classification의 pipleline
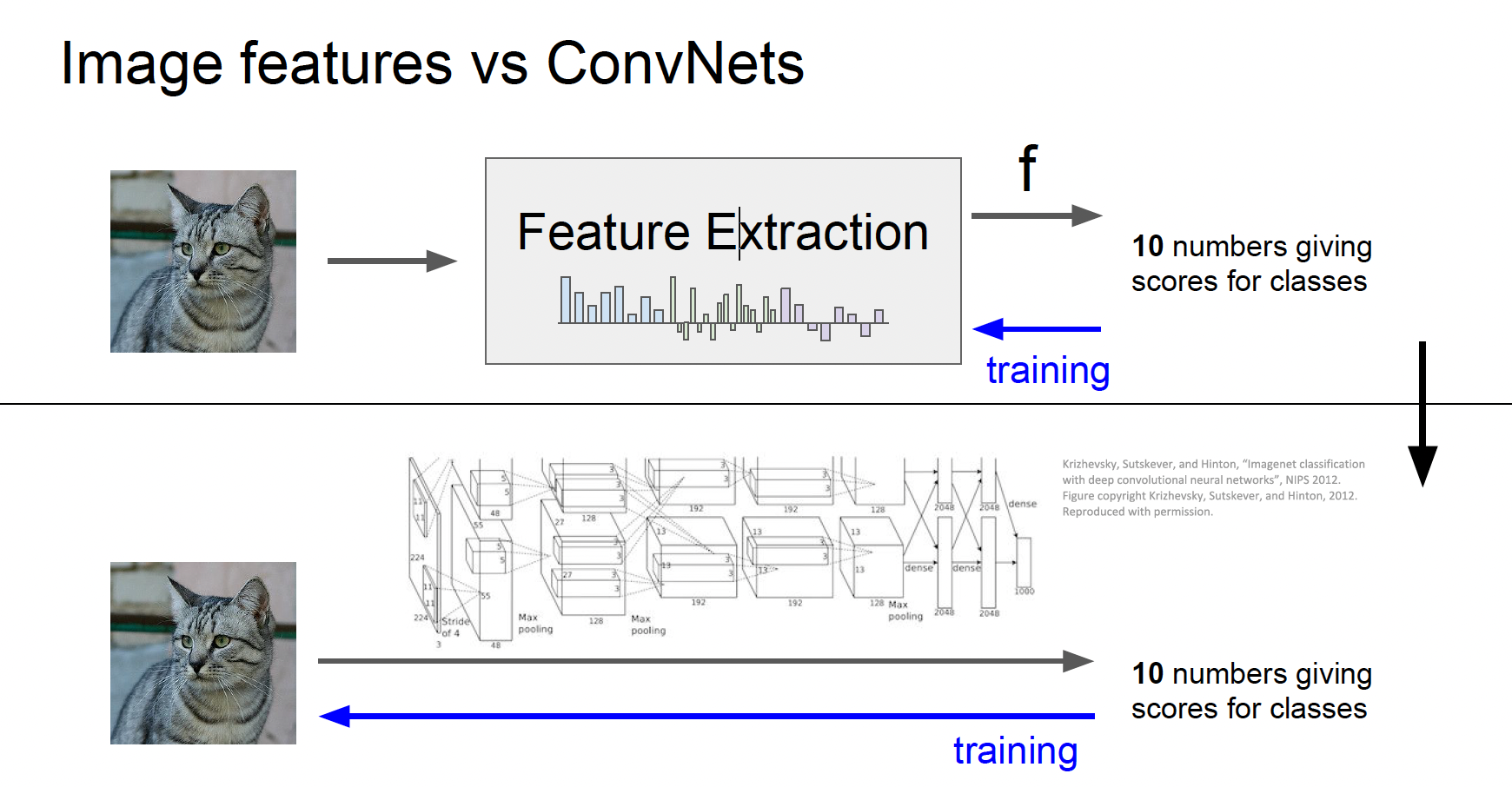
5~10년 전까지만 해도 이미지를 입력받으면 BOW나 HOG와 같은 다양한 특징 표현을 계산하고, 계산한 특징들을 한데 모아 연결해서, 추출된 그 특징들을 Linear classifier의 입력으로 사용했다.
특징이 한번 추출되면 feature extractor는 classier를 트레이닝하는 동안 변하지 않았고 트레이닝 중에는 오직 Linear classifier만 훈련 되었다.
CNN, DNN에서 다른 점은 이미 만들어 놓은 특징들을 쓰기 보다는 데이터로부터 특징들을 직접 학습하려 한다는 것이다.
그렇기 때문에 raw 픽셀이 CNN에 그대로 들어가고 여러 레이어를 거쳐서 데이터를 통한 특징 표현을 직접 만들어낸다.
따라서 Linear classifier만 훈련하는게 아니라 가중치 전체를 한꺼번에 학습하는 것이다.
