

L2 regression과 L1 regression
Linear classification의 관점에서 w1와 w2는 같음. 내적은 같기 때문이다.
그러나 L2 regression은 w2를 더 선호할 것이다.
왜냐면 L2 regression에서는 w2가 더 norm이 작기 때문에
그러니 L2 Regression은 분류기의 복잡도를 상대적으로 w1와
w2중 어떤 것이 더 coarse한지를 측정함.
Linear classification에서 W가 의미하는 것은, "얼마나 x가
Output Class와 닮았는지" 이다.
그러니 L2 Regression은 x의 모든 요소가 영향을 줬으면 하는 것이다.
반면 L1 Regularization의 경우에는 정 반대이다.
L1 Regularization을 쓰게 되면 W2보다는
W1을 더 선호하게 된다.
L1 Regularization은 가중치 W에 0의 갯수에 따라
모델의 복잡도를 다룬다.
L1에 대한 일반적인 직관은 "일반적으로 L1은 sparse한 solutions을 선호한다"는 것이다.
그리고 이것은 W의 요소 중 대부분이 0이 되게 할 것이다.
그렇게 때문에 L1이 "복잡하다"고 느끼고 측정하는 것은
0이 아닌 요소들의 갯수가 될 수 있다.
반면 L2의 경우에는 W의 요소가 전체적으로 퍼져있을 때
"덜 복잡하다" 라고 생각하게 된다.
그러니 선택은 데이터와 문제에 달려 있다.
(사진의 경우엔 w1과 w2의 경우 L1의 값이 같음)
Softmax classifier (Multinomial Logistic Regression)

- multi-class SVM loss 외에도 인기있음 (사실 딥러닝에서는 더 자주 쓰이는)
- mulfi-class SVM의 경우에 우리는 그 스코어 자체는 크게 신경쓰지 않았지만, 이건 스코어 자체에 추가적인 의미를 부여함 그래서
- softmax라고 불리는 함수(네모박스 친)를 이용해서 스코어를 가지고 클래스 별
확률 분포를 계산함 - 결국 우리가 원하는 것은 정답 클래스에 해당하는 클래스의 확률이 1에 가깝게 계산되는 것
- Loss는 "-log(정답클래스확률)"

스코어를 지수화, 정규화 한 후 정답 스코어에만 -log를 씌움
이걸 softmax loss, 다항 로지스틱 회귀라고 한다.
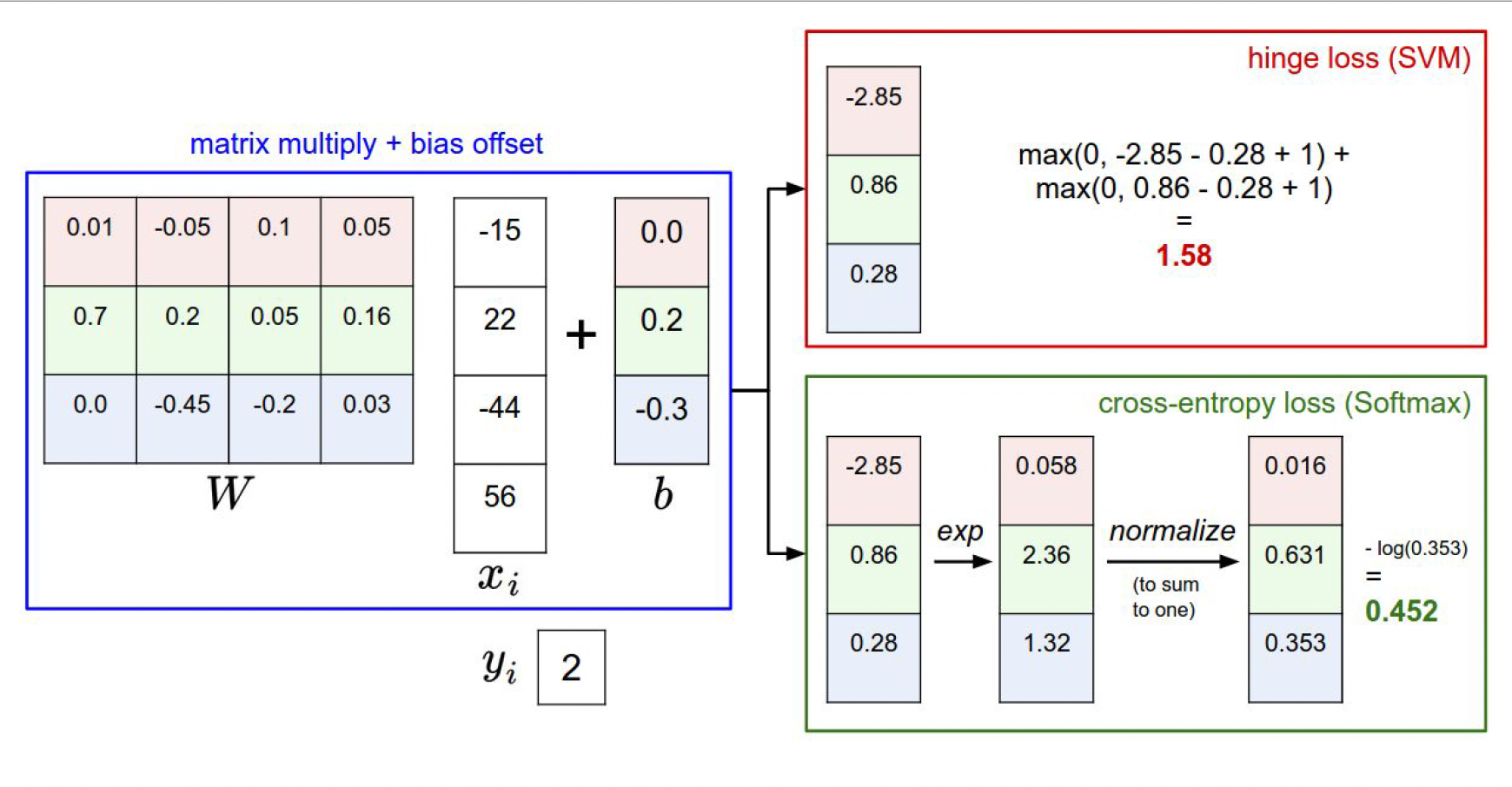
- 두 손실 함수의 차이점은 바로 "얼마나 구린지" 를 측정하기 위해
스코어를 해석하는 방식이 조금 다르다는 것 - SVM에서는 정답 스코어와, 정답이 아닌 스코어 간의 마진(margins)을 신경 씀
- 반면 softmax (crossentropy) 는 확률을 구해서 -log(정답클래스) 에 신경을 씀
- SVM의 경우에는 일정 선(margins)을 넘기만 하면 더이상 성능 개선에 신경쓰지 않는다.
- 반면 softmax는 더더더더더좋게 성능을 높이려 할 것이다.
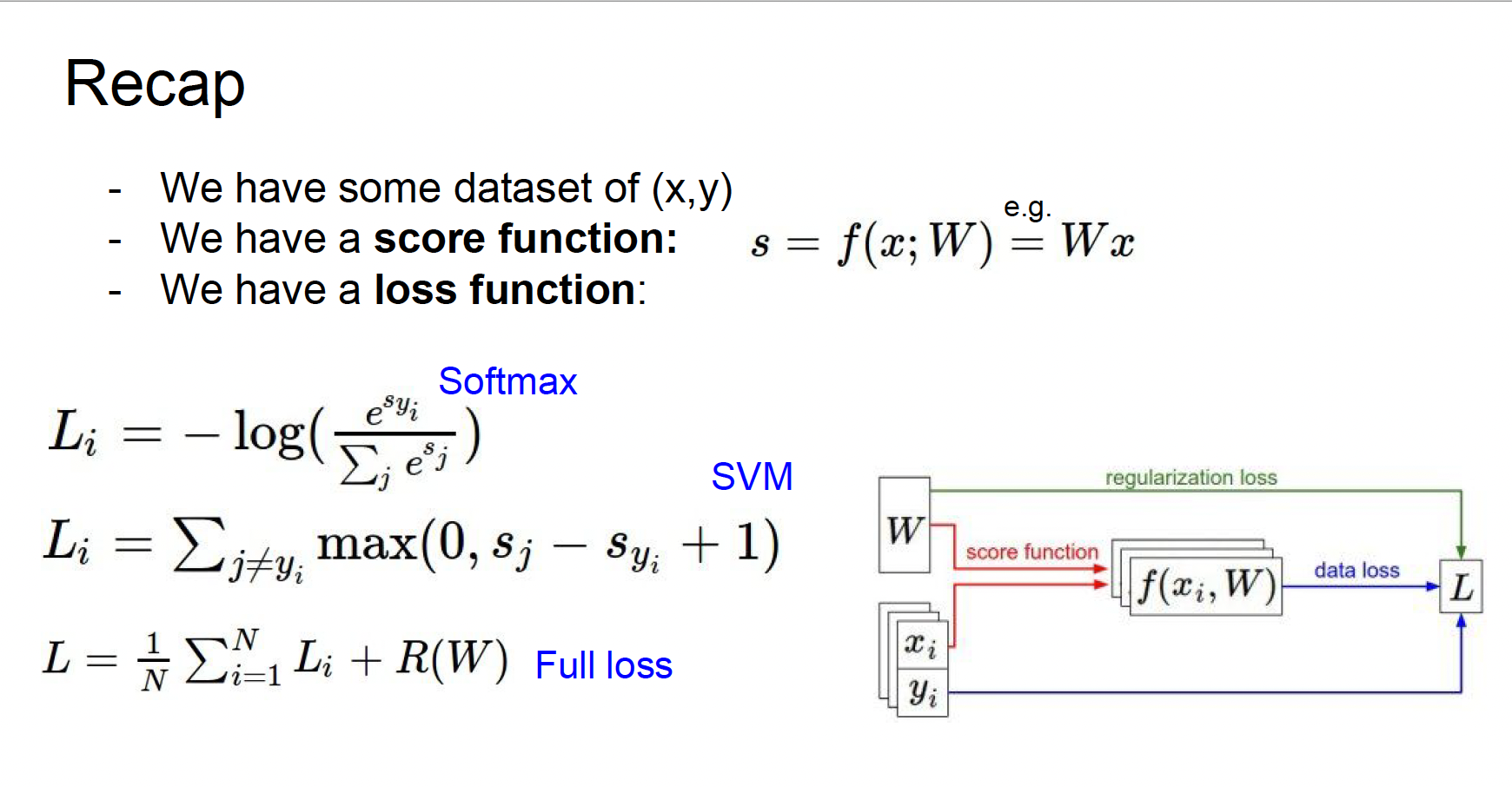
정리하자면,
1. 입력 x로부터 스코어를 얻기 위해 Linear classifier를 사용한다.
2. softmax, svm loss와 같은 손실함수를 이용해서, 모델의 예측값이 정답 값에 비해 "얼마나 구린지"를 측정한다.
3. 모델의 "복잡함" 과 "단순함" 을 통제하기 위해 손실 함수에 regularization term을 추가한다.
4. 이를 합쳐서, 최종 손실 함수가 최소가 되게 하는 가중치 행렬이자 파라미터인 행렬W를 구한다.
→ 4번은 어떻게? 어떻게 실제 Loss를 줄이는 W를 찾을 수 있지?
✨ Optimization (최적화) 을 통해!
