• 분류: Image Generative Model
• 저자: Ian j.Goodfellow, Jean Pouget-Abadie, …
• 소속: University of Montreal
• paper: Generative Adversarial Nets
• 키워드: GAN, Generative model, adversarial training

1. 연구 배경

1. 딥러닝이 발전했지만 생성 모델(generative models)은 계산적으로 어려운 문제
2. 대부분의 성공적인 딥러닝 모델은 판별 모델(discriminative models)로, 데이터 특정 속성 분류에 집중
3. 생성 모델의 목표: 주어진 데이터 분포를 학습하고 새로운 데이터를 생성
4. 그러나, 기존의 생성 모델은 주어진 데이터 분포를 학습하는 과정에서 어려움을 겪음

핵심 목표: 새로운 생성 모델 학습 방법 제안으로 복잡한 확률 계산 우회하기

2. 핵심 아이디어 및 방법론

GAN(Generative Adversarial Networks): 생성 모델(G)과 판별 모델(D)이 경쟁하는 적대적 학습(advversarial training)을 통해 학습하기

1) 구조

• 생성자(G): 무작위 노이즈를 입력 받아 실제 데이터와 유사한 샘플 생성

• 판별자(D): 주어진 데이터가 실제 데이터인지 생성된 데이터인지 판별
  ** 위 두 모델은 ‘미니맥스 게임(minimax game)’ 수행으로 서로 개선해나감
  (+) 미니맥스 게임(minimax game)

  • 두 플레이어가 경쟁하는 제로섬 게임의 한 형태
  • 생성자와 판별자 사이의 경쟁 과정
  • 수렴(균형점 찾기)
    G와 D가 최적화되면 내쉬 균형(Nash Equilibrium)에 도달
    이상적인 경우: G가 실제 데이터 분포를 완벽하게 학습하는 경우
    -> D는 더 이상 G와 실제 데이터를 구별하지 못함
    => D는 모든 입력에 대해 0.5 출력

• 목적 함수
  $minmax V(G, D) = E_x ~ p_{data}(x)[log D(x)] + E_{z ~ p_z{z}}[log(1-D(G{z}))]$

• 학습 과정
  D는실제 데이터와 G가 생성한 데이터를 구분하도록 학습됨
  G는 D를 속일 수 있도록 학습됨(즉, D가 G의 출력을 실제 데이터로 분류하도록 유도)
  -> G는 실제 데이터 분포와 매우 유사한 데이터를 생성하도록 발전

3. 실험 및 핵심 작업

1) 사용 데이터

• MNIST: 손글씨 숫자 데이터셋
• Toronto Face Database(TFD): 얼굴 이미지 데이터셋
• CIFAR-10: 일반 객체 이미지 데이터셋

2) 모델 구조

• G(생서자): 다층 퍼셉트론(MLP) 기반, 랜덤 노이즈를 입력 받아 데이터셋 생성
• D(판별자): 다층 퍼셉트론(MLP) 기반, maxout 활성화 함수 사용
• 훈련 기법
  • 역전파와 드롭아웃 활용으로 모델 최적화
  • 판별자 D는 k번 업데이트 후 생성자 G를 한 번 업데이트하는 방식으로 훈련
  • 생성자의 손실 함수: log(1-D(G(z)) 대신 log D(G(z))사용으로 안정적인 학습 유도

3) 전처리

• 노이즈 z를입력으로 사용하여 G의출력 다양화
• parzen window 기반 로그 가능도를 이용해 모델 성능 평가
  (+) 로그 가능도(log-likelihood)

  • 확률 분포의 적합도를 평가하는 주요 방법
  • 주어진 데이터가 모델에서 생성될 확률 측정
    ‘학습된 데이터 분포 $P_g(x)$가 실제 데이터 분포 $P_{data}(x)$와 얼마나 유사한지?’

(+) 생성 모델에서 로그 가능도로 성능 측정하기: parzen windown density estimation

1. 모델 G에서 샘플 $x$ 생성 -> 샘플 집합 ${x_g}$
2. 가우시안 parzen window 방식으로 학률 밀도 함수 근사
   $P_g(x) ≈ \frac{1}{N}\Sigma^{N}_{i=1}N(x|x_g^{(i)}, \sigma^2I)$
3. 테스트 데이터 $x_{test}$의 로그 가능도 평가
   $LL(x_{test}) = \Sigma^N_{i=1}logP_g(x_{test})$
4. $\sigma$(커널 너비)는 검증 데이터로 최적값 찾기

4. 결과 및 분석

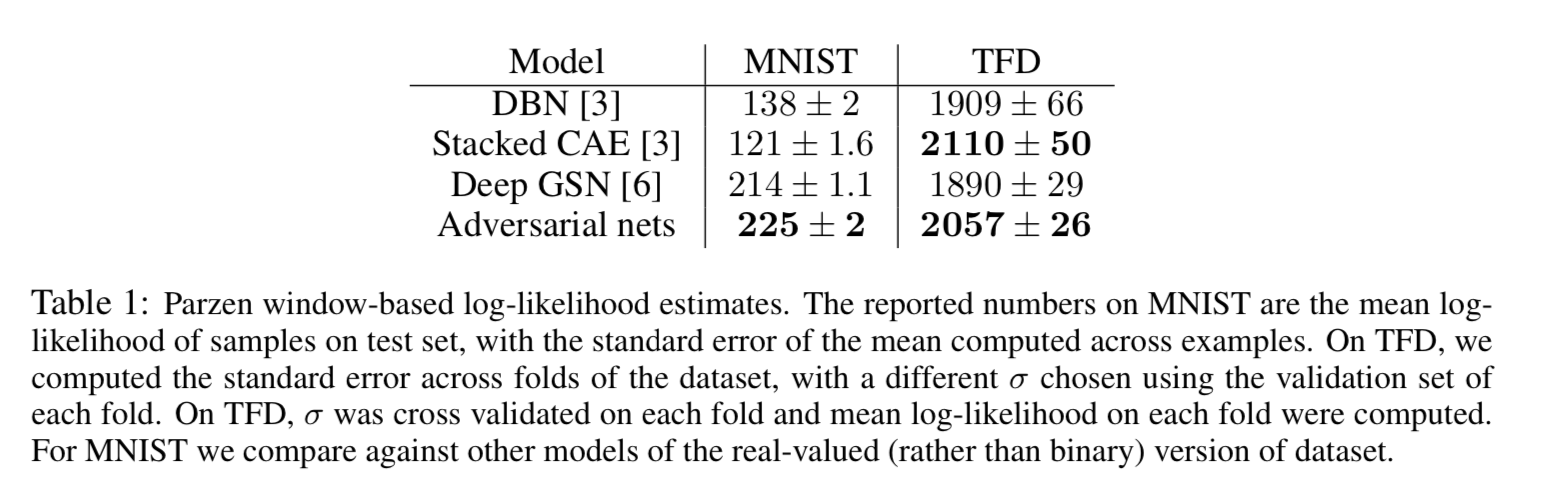
• CIFAR-10에서도 질적으로 우수한 샘플 생성
  

장점

• 학습 과정에서 마르코프 체인없이 샘플 생성 가능

  <마르코프 체인>

  1. 반복적이고 계산량 많음
  2. 수렴을 보장할 수 없음

• 명시적인 확률 모델없이 학습 가능
• 특정 조건 추가로 조건부 생성 모델을 만들 수 있음

단점

• 명시적 확률 분포 $P(x)$ 표현 불가
• 생성자와 판별자 간 학습 균형을 맞추는 것이 어려움
  (판별자가 너무 강해지면 생성자가 학습을 못함)
• Helutica Scenario 문제: G가 다양한 출력을 생성하지 않고 특정 데이터에 과적합됨

5. 결론 및 향후 연구 방향

• 조건부 생성 모델
  특정 속성을 조정하여 생성할 수 있도록 확장(conditional GAN)
• 적응적 학습 기법
  G와 D의 균형을 맞추는 새로운 학습 전략 개발
• 효율적인 샘플링
  GAN이더 높은 차원의 데이터에서도 효율적으로 학습할 수 있도록 개선
• semi-supervised learning
  GAN의 D로 라벨이 부족한 환경에서 성능 향상 가능