(딥러닝을 처음 배운다 ... 생각하고 정리하기)

Parametric Functions

Linear Function

딥러닝 관점에서 생각하는 두 개의 일차함수가 서로 다른 함수인 이유:

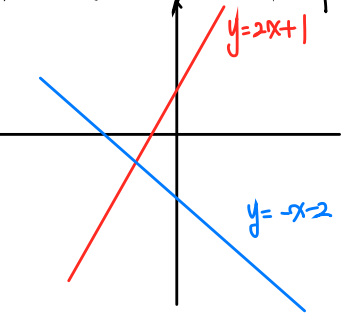
빨간색 그래프와 파란색 그래프가 다른 이유는?

동일한 입력값->다른 출력값 을 갖기 때문

여기서 공통점은 둘다 일차함수 y=ax+b 라는 것
y=ax+b 여기에서 바꿀 수 있는 변수는 a, b <- parameter

f(x ; a,b) = ax+b
뜻: x는 입력, a,b는 학습이 가능한 parameter

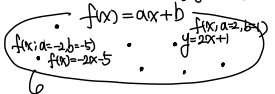
이렇게 무수히 많은y=ax+b 꼴의 집합들이 있다.
딥러닝이란, 여기서 우리가 원하는 parameter를 찾아내는 것

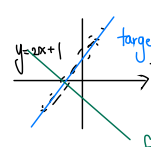
위 그래프에서 검정색 점점점에 가까운 그래프는 파란색일까 초록색일까?
데이터를 잘 반영하는 그래프는 파란색, target function 이라고 한다.
예를들어, 파란색 그래프가 y=2x+1 이라면 a=2, b=1 이라는 타겟값을 갖는다.

하지만 우리가 학습을 할 때에는, 정확히 파란색 그래프의 parameter들을 알지 못하니까,
초기값으로 아무 값을 집어넣는다. 예를들어 a0=-1, b0=-2 이런식으로...

이 값들이 타겟값이 되려면 학습을 통해 가능하다!

학습이란, a0과 b0이 각각 타겟값인 a와 b에 가까워지도록 만드는 것

그래프 관점에서 보지말고, parameter관점으로 볼 것!

Gradient-based Learning

만약

이런 그래프가 있다고 하자.

ㅋㅋㅋㅋㅋ 그림은 작지만.. 이렇게 생겼을 것이다. 아래로 볼록(convex)함수!
여기서 함수값을 최소로 하는 x값 = $\underset{x}{argmin}f(x)$ 을 찾는다면, x=0이 될 것이다.

ex)

여기서 $x^*$값은 얼마인가? -2, 3!
즉,

이렇게 된다!

Deep Learning에서의 순간 변화율(미분계수)

미분이라고 하면 일반적으로 생각하는 개념 => $\displaystyle \lim_{\bigtriangleup x\to 0}\frac{\bigtriangleup y}{\bigtriangleup x}$

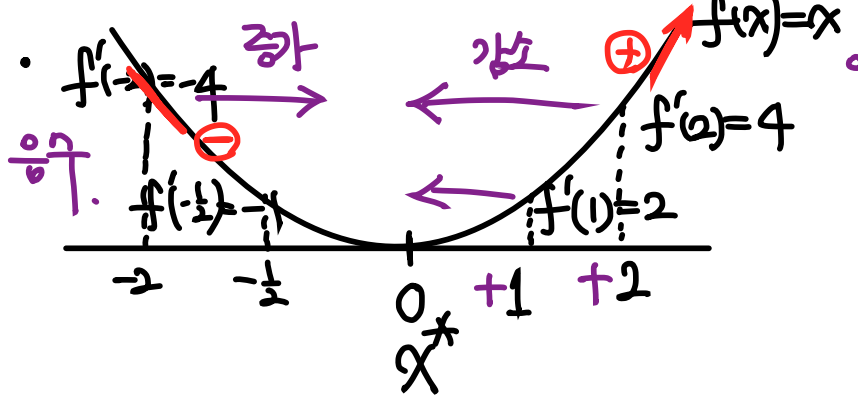
위 그래프를 살펴보자.

입력이 변할 때 출력이 어떻게 변하는가?

라는 질문에 대답해보자.

라는 그래프에서 x*의 값을 1 혹은 2 를 집어넣으면 함수의 최소값을 구하기 위해서는 x를 감소하는 방향으로 이동해야 한다.
반대로, x*의 값을 음수인 -2, -1/2라고 한다면, 함수의 최소값을 구하기 위해서 x는 증가하는 방향으로 이동해야 한다.

즉 여기서 알 수 있는 패턴은,

미분계수의 부호 $\leftrightarrow$ x*로 향하는 방향

$sgn(x)$라는 함수를 배운 적이 있을 것이다.
바로 부호를 반환하는 함수인데,

이런 형식이다. 나중에 뒤에서 출현하니 참고해두자!

코딩 실습

$f(x)=\frac{1}{10}(x-1)^2$일 때, 임의의 점 x에서 출발하여 x:= x-f'(x)를 반복하면 x는 x*에 가까워짐을 확인하고 시각화해보자.

import matplotlib.pyplot as plt
import numpy as np

def f(x):
    return 1/10*(x-1)**2

def df(x):
    return 1/5*(x-1)

x = 10  # 임의의 x에서 시작

x_vals = [x]
y_vals = [f(x)]

for _ in range(100):  # 100번 반복
    x = x - df(x)
    x_vals.append(x)
    y_vals.append(f(x))

plt.figure(figsize=(12, 8))
plt.plot(x_vals, y_vals, 'o-')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
plt.show()

결과값은 깜빡하고 저장을 못했는데,,, 알아서 확인해보자

Singlevariate Linear Regression

Loss function

모델의 출력이 실제 데이터와 비슷해지려면?

대답해보자.

아마 모델의 출력과 실제 데이터의 차이가 줄어야 할 것이다.
모델의 출력과 실제 데이터의 차이를 손실 이라고 한다.

이를 수치화 할 수 있을까?

우리가 알고 있는 건Squared Error라고 하는 $(\hat{y}-y)^2$ 일 것이다. 그렇다면 왜 Absolute Error 인 $|\hat{y}-y|^2$는 안될까? 정답은 없다.
(여기서 $\hat{y}$ 은 예측값(바뀔 수 있다), y는 실제값(바뀔 수 없다))
전자는 아웃라이어에 대해 민감해지고, (아웃라이어 : 튀는 값)
후자는 미분이 불가능한 값이 존재한다.

즉, 자신이 어떤 데이터를 사용하는지에 따라 다를 수 있다. 전자가 보편적으로 쓰이지만 옳은 것은 아니다.

다시 처음으로 돌아와서, 우리가 예측한 값인 $\hat{y}$는 이렇게 적을 수 있겠다.
$\hat{y}=ax+b$
그리고 loss function은, $J=L(\hat{y},y)=(\hat{y}-y)^2$
즉, $\hat{y}=ax+b$이므로, a와 b를 바꾸면 $\hat{y}$값을 바꿀 수 있게 된다.

식으로 좀 더 자세히 표현하자면 이렇게,

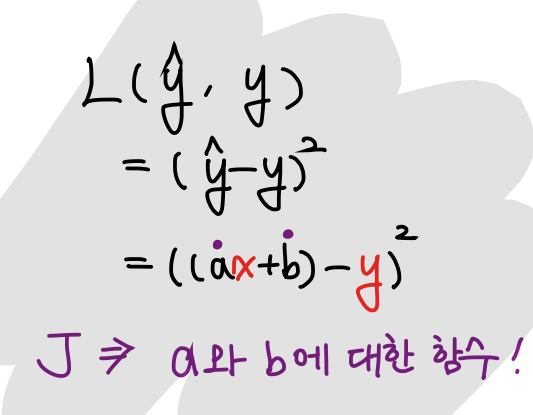
parameter를 바꾸면 같은 x에 대해 Loss를 줄일 수 있다.

처음에 배웠을 땐 x와 y에 대한 방정식인 줄 알았는데, 알고보니 계수가 변수가 되는 !!! 그래서 헷갈릴 수 있다. 주의하자!

우리는 더 많은 데이터와 부합하는 하나의 함수식을 찾아야 하므로 J를 최소화하는 방향으로 파라미터들을 업데이트하게된다.
우리가 알고싶은 건 Loss함수값을 최소로 만드는 타겟값인 $a^*$과 $b^*$

즉, 우리에게 필요한 것은 Loss함수에서의 a와 b에 대한 미분값 $\frac{\partial J}{\partial a}$와 $\frac{\partial J}{\partial b}$이다.

여기서 좀 더 자세히 설명하면, a,b가 움직일 방향이 필요한데, 아까 sgn(x)를 설명하면서 "x*로 향하는 방향과 미분계수의 부호는 반대"라는 얘기를 했었다.
즉, 우리는 함수값을 감소시키기 위해서는 $-sgn'(x)$가 필요하게 된다.

와 같은 업데이트 공식을 사용해서 a와 b의 타겟값에 가까워지는 값을 찾아낼 수 있다.

위 두 식을 반복하면, 각각 $a^*$와 $b^*$에 가까워진다.

코드 실습

함수 $f(x) = \frac{1}{10}(x - 1)^{2}$로 주어졌을 때, 임의의 $x$에서 출발하여

를 반복하면, $x$는 $x^{*}$에 가까워짐을 확인하고, 시각화(그래프 + update되는 점들)하세요.

import numpy as np
import matplotlib.pyplot as plt

# target function의 파라미터
a_star = 2
b_star = 1
n_samples = 100

def make_dataset(n_samples, a_star, b_star):
    X = np.random.normal(loc=0, scale=1, size=(n_samples,))
    Y = a_star * X + b_star
    noise = 0.3*np.random.normal(loc=0, scale=1, size=(n_samples,))
    Y = Y+noise
    return X, Y

x, y_star = make_dataset(n_samples, a_star, b_star)

class LinearFunction:
    def __init__(self, a,b):
        self.a, self.b = a,b

    def __call__(self, x):
        return self.a * x + self.b

    def update_params(self, dloss_da, dloss_db, lr):
        self.a = self.a - lr * dloss_da
        self.b = self.b - lr * dloss_db

    def get_params(self):
        return self.a, self.b

# 학습률
lr = 0.001

# 반복 횟수
epochs = 1000

# 파라미터의 변화를 저장할 리스트
a_vals = []
b_vals = []

model = LinearFunction(a=-2,b=-1)

# 경사 하강법
for _ in range(epochs):
    for x_sample, y in zip(x, y_star):
        # 예측값
        y_pred = model(x_sample)
        loss = (y_pred-y)**2

        # 그래디언트
        dloss_da = 2*x_sample*(y_pred-y)
        dloss_db = 2*(y_pred-y)

        model.update_params(dloss_da, dloss_db, lr)

    a,b = model.get_params()

    # 파라미터 값 저장
    a_vals.append(a)
    b_vals.append(b)

# 파라미터의 변화를 시각화
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(a_vals)
plt.title("a values")
plt.subplot(1, 2, 2)
plt.plot(b_vals)
plt.title("b values")
plt.show()

print("Final values of a and b: ", a, b)

Learning rate는 안배웠는데, 여기서 안넣으면 값이 확 발산되어서 안된다 어쩔 수 없이 도입...

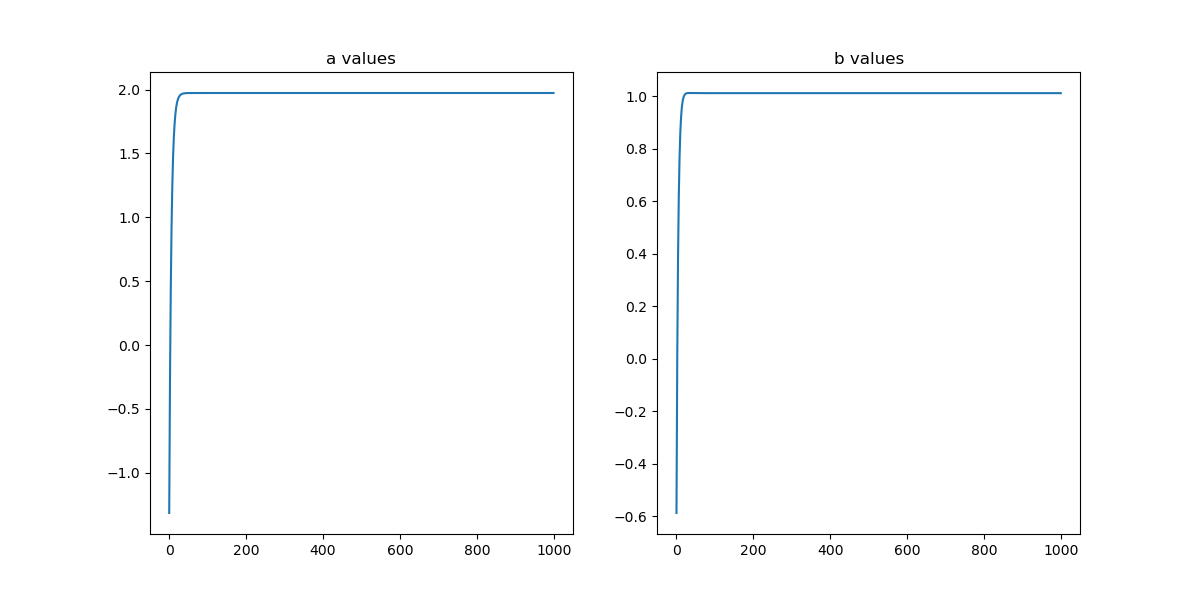
이런 그래프값을 얻었다!

전체적으로 미분이 필요한 이유를 정확히 이해했고 parameter들이 왜 중요한지 알게 되었다.
코드로 실습을 많이 해야 할 듯!