Deep Neural Network-Application

여기에서는 각각의 정의된 함수의 코드를 설명하지 않는다. 함수의 내용을 알기 위해서는 이전 글을 참고하길 바란다.

이전 글에서 설명했던 함수들을 가지고 전체 DNN모델을 만들어보자. 잘 이해했다면 이번 내용은 어렵지 않다.

Packages

import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v3 import *
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

Load Data

이번 글에서는 "고양이 vs 안고양이" 데이터셋을 사용할 것이다. 이전에 Logistic Regression 으로 구현했을 때에는 마지막에 70%의 정확도가 나왔는데, 이번에는 DNN으로 구현해보도록 하겠다.

train_x_orig, train_y, test_x_orig, test_y, classes = load_data()

이제 샘플 하나를 꺼내서 어떤 그림인지 살펴보자.
여기서는 21번째 샘플을 확인해보도록 하겠다.

index = 21
plt.imshow(train_x_orig[index])
print ("y = " + str(train_y[0,index]) + ". It's a " + classes[train_y[0,index]].decode("utf-8") +  " picture.")

인덱스값이 0인 안고양이 사진이 나왔다.

Reshape하기 전에 shape먼저 알아보자.

m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]

print ("Number of training examples: " + str(m_train))
print ("Number of testing examples: " + str(m_test))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_x_orig shape: " + str(train_x_orig.shape))
print ("train_y shape: " + str(train_y.shape))
print ("test_x_orig shape: " + str(test_x_orig.shape))
print ("test_y shape: " + str(test_y.shape))

위와 같은 출력값이 나온다.
트레이닝 샘플은 209개, 테스트 샘플은 50개,
이미지 사이즈는 64*64이다.

이제 이미지 전처리를 같이 해야 한다.

train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T   # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T

train_x = train_x_flatten/255.
test_x = test_x_flatten/255.

print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))

전처리 후의 출력값이다.
12288은 이미지 사이즈인 64 x 64 x 3을 계산한 값이다.

2-layer Neural Network

이전에 만들었던 함수들을 정리해보자.
def initialize_parameters(n_x, n_h, n_y): return parameters
def linear_activation_forward(A_prev, W, b, activation): return A, cache
def compute_cost(AL, Y): return cost
def linear_activation_backward(dA, cache, activation): return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate): return parameters

위 함수들을 가지고 two-layer model을 만들어보자.
model은 고정이기 때문에 먼저 constants들을 정의하고 시작한다.

n_x = 12288     # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
learning_rate = 0.0075

모델을 구축해보자.

def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):

    np.random.seed(1)
    grads = {}
    costs = []
    m = X.shape[1]
    (n_x, n_h, n_y) = layers_dims
    
    #initialice parameters dictionary
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    #get parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    #Loop(gradient descent)
    for i in range(0, num_iterations):
        
        #forward propagation
        A1, cache1 = linear_activation_forward(X, W1, b1, activation="relu")
        A2, cache2 = linear_activation_forward(A1, W2, b2, activation="sigmoid")
        
        #compute cost
        cost = compute_cost(A2, Y)
        
        #initialize backward propagation
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        #backward propagation
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation="sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation="relu")
        
        #set gradients
        grads['dW1'] = dW1
        grads['db1'] = db1
        grads['dW2'] = dW2
        grads['db2'] = db2
        
        #update parameters
        parameters = update_parameters(parameters, grads, learning_rate)
        
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        #print the cost every 100 iterations
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)

    return parameters, costs

이제 plt을 이용해서 cost를 그리는 함수도 정의해보자.

def plot_costs(costs, learning_rate=0.0075):
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()

모델 정의가 끝났다.
이제 우리가 가지고 있는 데이터를 모델 안의 변수들로 넣어 실행해보자. 그와 동시에 cost도 뽑아내보도록 하겠다.

parameters, costs = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)

plot_costs(costs, learning_rate)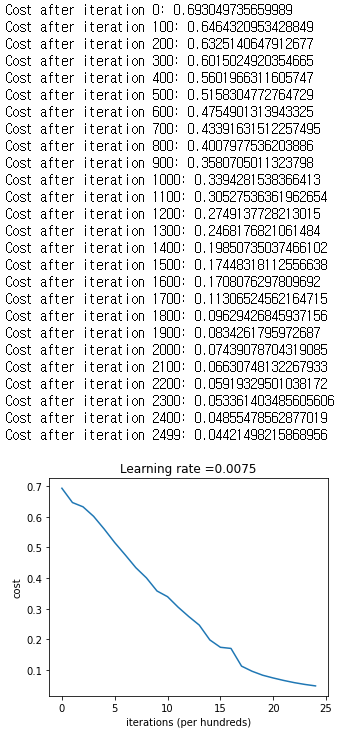

실행하는데 5분정도의 시간이 소요된다. cost가 점점 줄어드는 것을 확인할 수 있다.

train sample을 가지고 prediction을 해 보자. 아마 1과 가까운 숫자가 나올 것이다.

predictions_train = predict(train_x, train_y, parameters)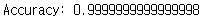

같은 방법으로 test sample에도 해보자. 70%보다 높은 정확도가 나왔으면 좋겠다.

predictions_test = predict(test_x, test_y, parameters)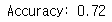

정리하자면, Logistic regression에서는 70%의 정확도를,
2-layer에서는 72%의 정확도를 출력했다.

다음으로는 본격적으로 L-layer에서의 모델을 구축하고, 몇 퍼센트의 정확도가 나오는지 확인해보자.

L-layer Neural Network

마찬가지로 이전에 만들어 놓았던 함수들을 꺼내와보자.
def initialize_parameters_deep(layers_dims): return parameters
def L_model_forward(X, parameters): return AL, caches
def compute_cost(AL, Y): return cost
def L_model_backward(AL, Y, caches): return grads
def update_parameters(parameters, grads, learning_rate): return parameters

모델을 구축하기 전, constants를 정의한다.

layers_dims = [12288, 20, 7, 5, 1] #  4-layer model

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    np.random.seed(1)
    costs = [] 
    
    #init parameters
    parameters = initialize_parameters_deep(layers_dims)
    
    #Loop(gradient descent)
    for i in range(0, num_iterations):
        
        #forward propagation
        AL, caches = L_model_forward(X, parameters)
        
        #cost
        cost = compute_cost(AL, Y)
        
        #backward propagation
        grads = L_model_backward(AL, Y, caches)
        
        #update parameters
        parameters = update_parameters(parameters, grads, learning_rate)
        
        #print cost every 100 iterations
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)
    
    return parameters, costs

마찬가지로 그래프를 그려서 매 100개의 iteration마다 cost를 확인해주자.

parameters, costs = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)
plot_costs(costs, learning_rate)

조금의 인내심이 필요한 작업이다.
아래와 같은 결과가 나온다.

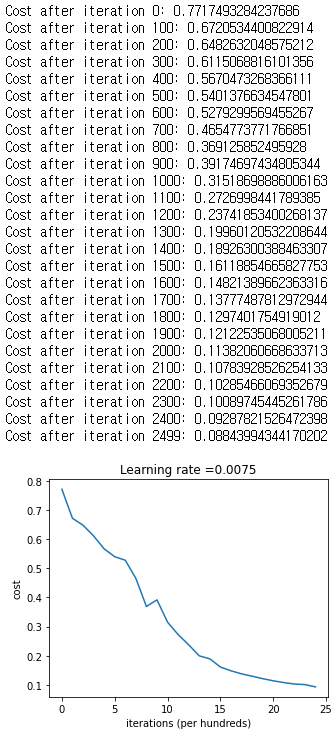
이제 train sample에 대해 정확도를 확인해보자.

pred_train = predict(train_x, train_y, parameters)

역시 1과 가까운 숫자가 나왔다.
다음으로는 test sample을 가지고 정확도를 확인해보자.

pred_test = predict(test_x, test_y, parameters)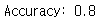

80%라는 높은 정확도가 나왔다.

Analysis

마지막으로, 컴퓨터가 잘못 판단한 그림들을 확인해보자.

print_mislabeled_images(classes, test_x, test_y, pred_test)

등등이 있다.