1.4절 일차결합과 연립일차방정식

1.4 Linear combinations and systems of linear equations

일차결합(Linear combination)

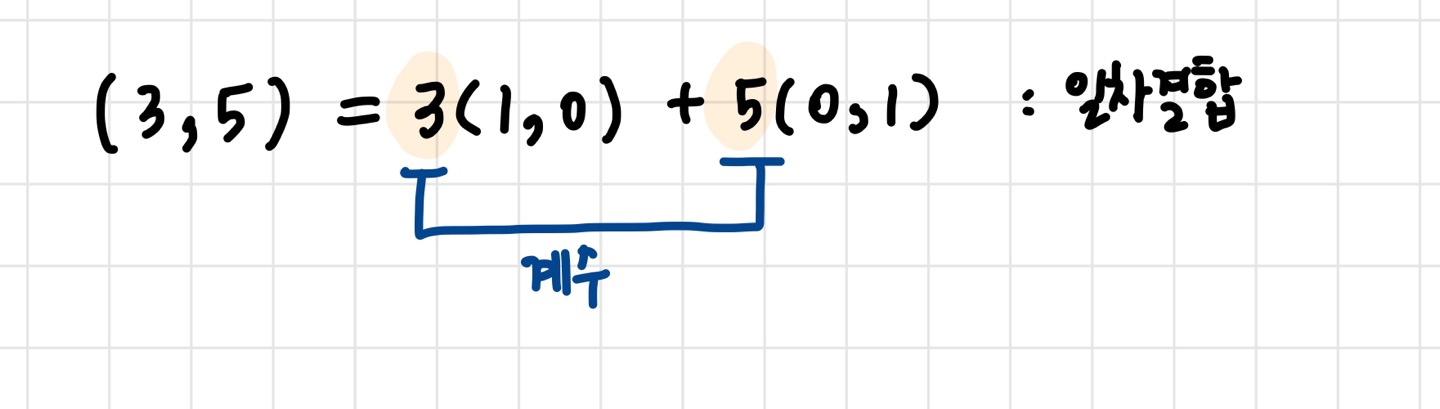
유한개의 벡터 $u_1,u_2,\dotsb,u_n \in S$와 scaler $a_1, a_2, \dotsb,a_n$ 에 대해 $v = a_1u_1 + a_2u_2+\dotsb+a_nu_n$을 만족하는 벡터 $v\in\mathbf{V}$는 $S$의 일차결합이라고 한다.

이 때, $v$는 벡터 $u_1,u_2,\dotsb,u_n$의 일차결합이고 $a_1, a_2, \dotsb,a_n$ 은 일차결합의 계수이다.

✏️Ex 문제
$2x^3-2x^2+12x-6$이 $x^3-2x^2-5x-3$과 $3x^3-5x^2-4x-6$의 linear combination으로 표현이 가능?

생성공간(span)

벡터공간 $V$의 공집합이 아닌 부분집합 $S$에서 가능한 모든 linear combinations의 집합을 $span(S)$라고 한다. 편의를 위해 $span(\empty) =$ {$0$} 으로 정의한다.

✅ Thm 1.5
벡터공간 $\mathbf{V}$의 임의의 부분집합 $S$의 생성공간은 $S$를 포함하는 $**\mathbf{V}$의 부분공간**이다.

증명)

✅ Thm 1.5
또한 $S$를 포함하는 $\mathbf{V}$의 부분공간은 반드시 $S$의 생성공간을 포함한다
증명)

✨ 정의
벡터공간 $\mathbf{V}$의 임의의 부분집합 $S$에 대하여 $span(S)=\mathbf{V}$이면 $S$는 $\mathbf{V}$를 생성한다. 이 경우에는 $S$의 벡터가 $\mathbf{V}$를 생성한다라고 말하기도 한다.

✏️Ex 문제
$M_{2\times2}(\mathbf{R}) = span \{\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix},\begin{bmatrix}1 & 1\\0 & 1 \end{bmatrix},\begin{bmatrix}1 & 0 \\1 & 1 \end{bmatrix}\}$ 생성 공간은?