Frequentist Probability vs Bayesian Probability
빈도론적 확률(Frequentist Probability):
확률은 객관적인 수치로, 반복 실험의 결과를 통해서만 정의된다.
매개변수 추정: 점 추정(Point Estimation)을 주로 사용하며, 신뢰구간을 통해 불확실성을 표현한다.
베이지안 확률(Bayesian Probability):
확률은 개인의 주관적인 신념을 수학적으로 표현한 것으로, 사전 확률(Prior Probability)과 사후 확률(Posterior Probability)을 포함한다.
매개변수 추정: 베이즈 정리를 사용하여 사전 확률을 업데이트하고, 이를 통해 매개변수의 분포를 추정한다.
"동전을 던졌을 때 앞면이 나올 확률은 1/2이다."
Frequentist Probability:
"동전을 던졌을 때 앞면이 나올 확률이 0.5라는 것은, 무한히 많은 동전 던지기 실험에서 앞면이 나오는 비율이 50%라는 것을 의미한다."
Bayesian Probability:
"동전을 던지기 전에 앞면이 나올 확률에 대해 어떤 사전 신념을 가지고 있다면, 던진 결과를 통해 그 신념을 갱신한다. 만약 동전을 여러 번 던져서 앞면이 자주 나온다면, 앞면이 나올 확률을 더 높게 갱신한다."
Significance of Bayesian Probabilty:
어떤 사건을 여러번 시행하기 어렵다면 베이지안과 같은 시선으로 바라보는 것이 합리적임.
사전 지식을 활용해 우리가 경험적으로 얻기 힘든 사건에 대해 확률을 추정하는 것이 필요.
Bayes' theorem
- 사건 θ를 원인, 사건 X를 결과 라고 생각
- 사전 확률 P(θ) : 결과가 나타나기 전에 결정되어 있는 원인(사건 θ)의 확률
- 우도 확률 P(X|θ) : 원인(사건 θ)가 발생하였다는 가정 하에 결과(사건 X)가 발생할 확률
- 사후 확률 P(θ|X) : 결과(사건 X)가 발생하였다는 가정 하에 원인(사건 θ)가 발생했을 확률
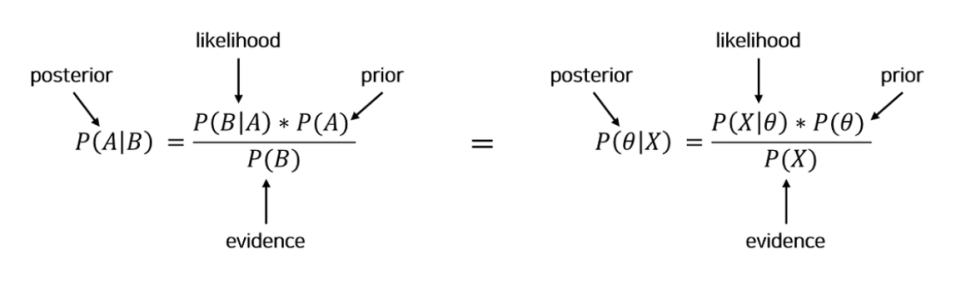
단순한 조건부 확률을 활용한 계산 식
예를 들어, 질병 검사에서 양성 반응이 나온 사건을 +, 실제 질병에 걸린 사건을 D로 정의하면,
- 관심 있는 사건 : 질병 검사의 양성 적중률 = P(D|+)
- 발병률 : P(D) = 0.01
- 병에 걸린 사람이 양성 : P(+|D) = 0.99
- 병에 걸리지 않은 사람이 양성 : P(+|D^c) = 0.10
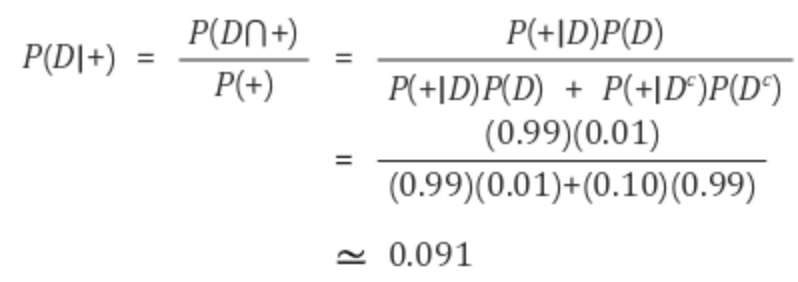
→ 질병 검사의 양성 적중률은 9.1%