🚀 Motivations

• Co-segmentation is intrinsically contextual:
  how a shape is segmented can vary
  depending on the set it is in.
  ➡️ Paper's network features an adaptive learning module
  to produce a consistent shape segmentation which adapts to a set

• Previous models on Deep Learning for shape segmentation,
  mostly trained to target a fixed set of semantic labels.
  Result in segmentation for a given shape is also fixed
  and can't be adaptive to the context of a shape set,
  a key feature of co-segemntation

🔑 Key Contribution

• Fisrt DNN for adaptive shape co-segmentation

• Novel and Effecitve group consistency loss
  based on low-rank approximations

• co-segmentation training framework
  that needs no GT consistent segmentation labels.

⭐ Methods

Overview

• Given an input set of unsegmented shapes,

1️⃣ First employ an "offline pre-trained" part prior network ➡️ to propse per-shape parts

2️⃣ Then, co-segmentation netowrk iteratively and jointly optimizes the part labelings
across the set subjected to a novel group consistency loss defined by matrix ranks.

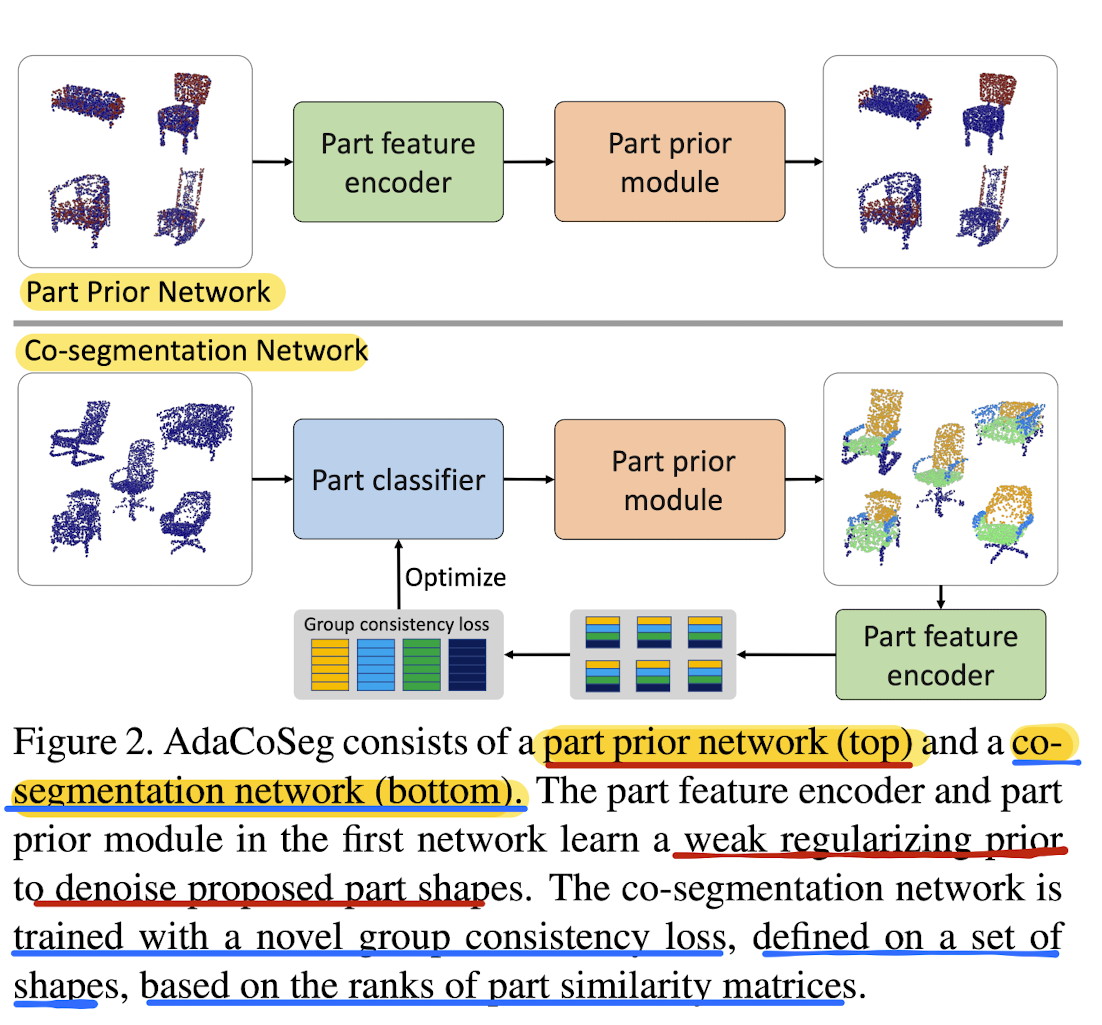
• AdaCoSeg: DNN for adaptive co-segmentation of a set of 3D shapes
  represented as point clouds
  📥 input: set of unsegmented shapes represented as point clouds
  📤 output: K-way consistent part labeling for the input set.
  without GT segmentations

Part prior network

"Learns to denoise an imperfectly segmented part"

📥 Input: 3D point cloud shape S
with noisy binary labeling,
where the FG represents an imperfect part

(Points belonging to the proposed part
constitute the FG (F ⊂ S),
while reamining points are BG (B = S \ F))

📤 Output: probability for each point (q ∈ S),
such that high probability points
collectively define the ideal, "clean" part
that best matches the proposed part,
thereby denoising the noisy foreground.

(= regluarized labeling leading to a refined part)

Architecture

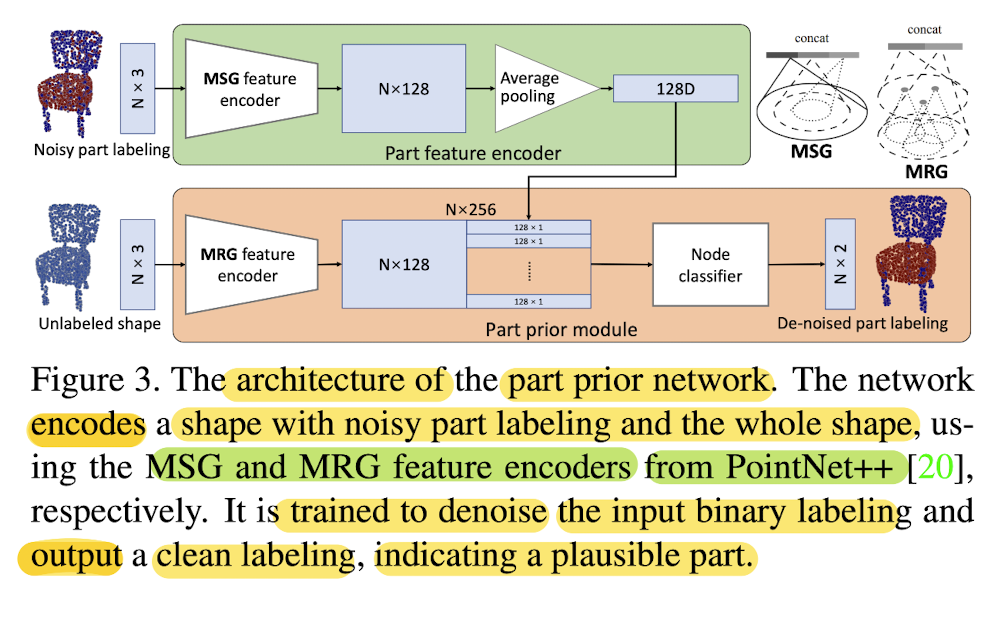
MSG & MRG for producing
two context-sensitive 128-D feature vectors

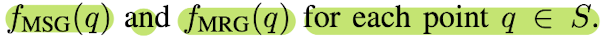
• MSG(multi-scale grouping):
  captures the context of a point at multiple scales,
  by concatenating feature
  over larger and larger nieghborhoods.

• MRG(multi-resolution grouping):
  computes a similar multi-scale feature,
  but the feature of a large neighborhood are computed recursively,
  from the feature of the next smaller neighborhood

• Paper average the MSG feature of FG points
  to obtain a robust descriptor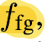
  which is concatenated with the MRG feature
  of each point
  to produce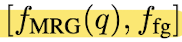
  pairs.

• Pairs are fed to a binary classifier with ReLU activation,
  where the output of the classifier
  indicates the "cleaned" FG and BG

🏋🏻‍♂️ Training Dataset: ComplementMe dataset(a subset of ShapeNet)

• Trained to denoise binary labelings

Learns
1) what a valid part looks like through training
on a labeling denoising task

2) Multi-scale and Part-aware shape feature
at each point,
which can be used later in co-seg network.

Co-segmentation network

📥 input: set of unsegmented shapes represented as point clouds

📤 output: K-way consistent part labeling for the input set.

• Learns the optimal network weights
  through back-propagation
  based on a group consistency loss
  defined over the input set.

• For each part generated by the K-way classifiction,
  a binary segmentation is formed and fed into
  the pre-trianed part prior network
  (1) to compute a refined K-part segmentation
  (2) to extract a part-aware feature for each segment.
  ➡️ Theses together form a part feature for each segment.

• Corresponding part features
  with the same label
  for all shapes in the set
  constitute a part feature matrix

• Then, weights of the co-seg network
  are optimized with objective
  to maximize the part feature similarity
  within on label
  and minimize the similarity across different labels.

• This amounts to minimizing
  the rank of the part feature matrix
  for each semantic label,
  while maximizing
  the rank of the joint part feature matrix
  for two semantic labels.

• The runtime stage of paper's pipeline
  jointly segments a set of unsegmented test shapes T = {S1, S2, ..., SN}
  to maximize consistency
  between the segmented parts.

• Outputs are compared across the test set
  to ensure geometric consistency of correspoinding segments:
  quantitative metric = group consistency energy,
  which is used as a loss function
  to iteratively refine the output of the network
  using back-propagation.

Architecture

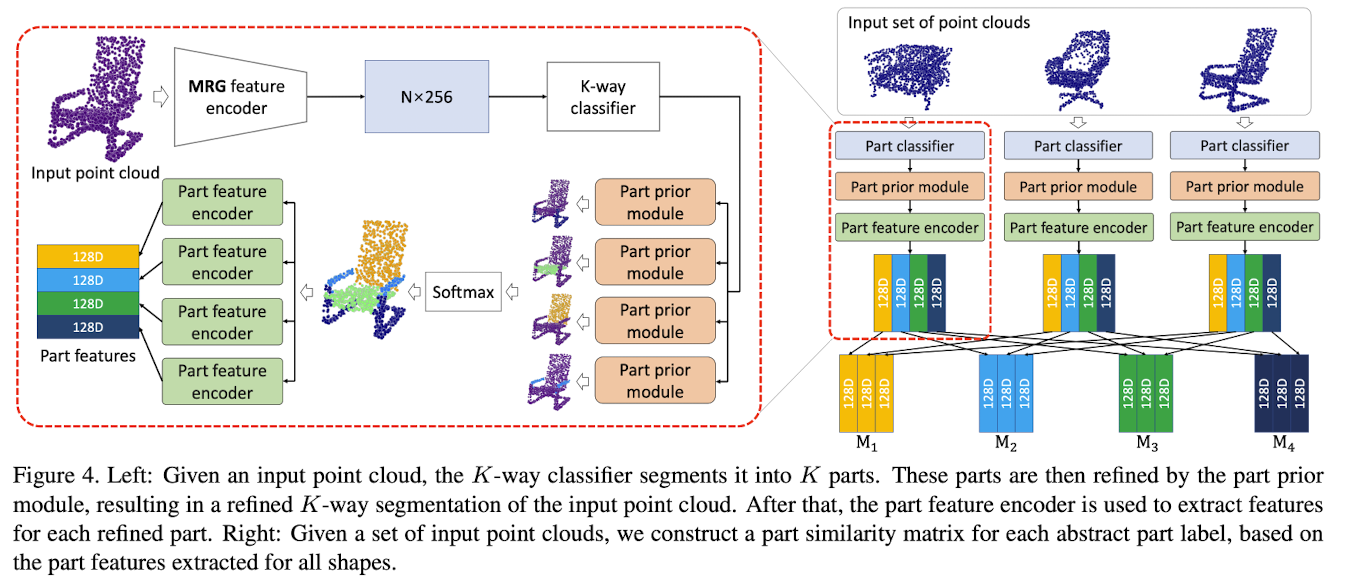
• Fisrt part: Classifier
  independently assigns one of K abstract labels {L1, L2, ..., Lk}
  to each point in each shape, with shared weights
  : the set of points in a shape with Label Li
  defines a single part with that label.

• Since classifier output may be noisy,
  pass the binary FG/BG map corresponding to each such part
  through the pre-trained offline denoising network(part prior network)

• Subsequent stages are deterministic and have no trainable parameters
  :used to compute the "group consisteny energy"(quantitative metric)

• First, MSG features of the FG points for each part
  are max-pooled to yield a part descriptor.

➡️ If segmentation is consistent across shape,
all parts with a given label Li should have similar descriptors
✅ Therefore, stack the descriptors for all parts
with this label from all shapes
in a matrix Mi, one per row,
and try to minimize its second singular value,
a proxy for its rank (low rank == more consistent)

➡️ Parts with different lables shoud be distnct,
so union of the rows of matrices Mi and M(i!=j) shoud have high rank.
✅ want to maximize the second singular value of concat(Mi, Mj),
where concat function constructs a new matrix
with the union of the rows of its inputs.

The overall energy function is:
(where rank function is the second singular value, computed by a SVD decomposition)

As this energy is optimized by gradient descent,
the initial layers of the network learn to propose
more and more consistent segmentations
across the test dataset.

Additionally, paper found that
gaps between segments of a shape
appeared frequently and noticeably before re-composition,
and were resolved arbitrarily with the subsequent softmax
➡️ added a second energy term
that penalzes such gaps

👨🏻‍🔬 Experiments Results

Discriminative power of matrix ranks

• To show matrix ranks provide a discriminative metric
• Hypothesis: matrix rank makie it easy
  to distinguish betweem collections
  with few distinct lables, and collections with many distinc labels.
  
• All part collections with more labels have a higher scores (Fig6. right)
• Conclustion: Rank-based metric accurately reflects consistency of a part collection.

Control, adaptivity, and generalization

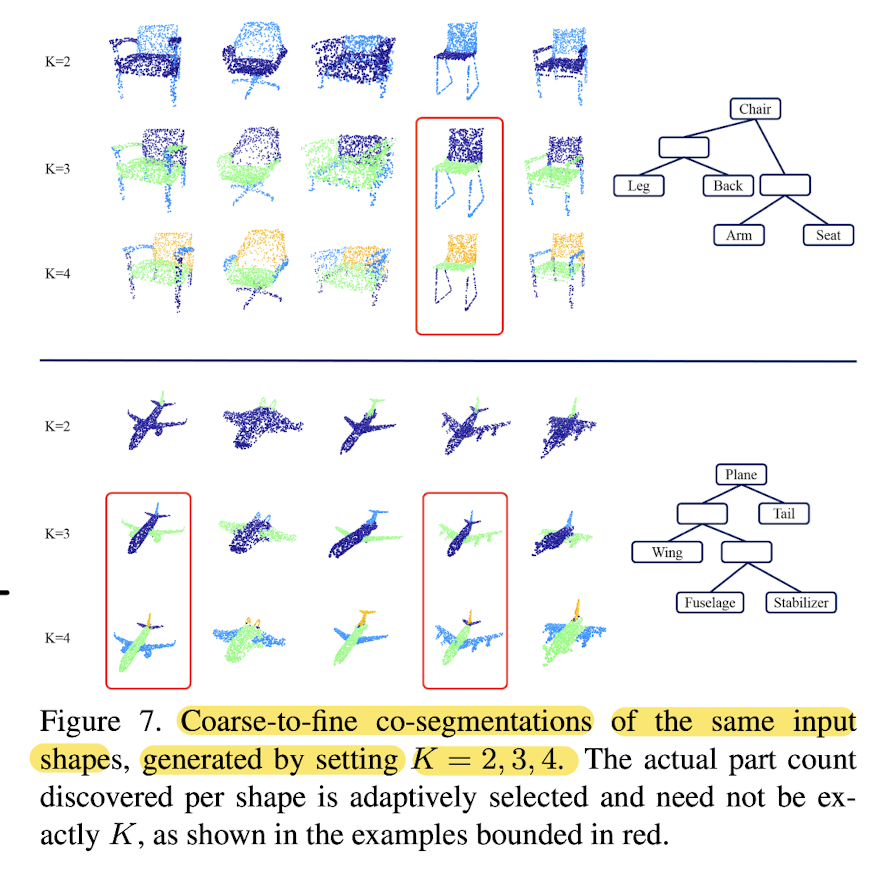
• Fig7. ➡️ co-seg of the same shapes
  for different values of K.
  Method produces coarse-to-fine part hierarchies.
  🔥However, this nesting structure is not guaranteed by the method, leave this as future work.

• Fig1. ➡️ Co-segmentations of two different chair collections, both with K = 4.
  The collection on the left has several chairs with arms:
  hench, the optimization detects arms
  as onf ot the prominent parts
  and groups all chair legs into a single segment.
  🆚 The other collection has no arms,
  hence the four part types are assigned to back,seat,front, and back legs.

Quantitative evalutation

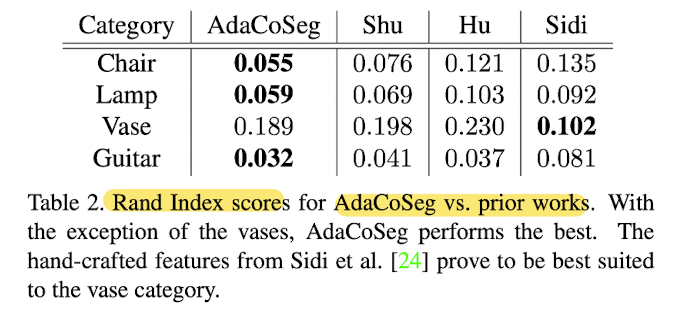
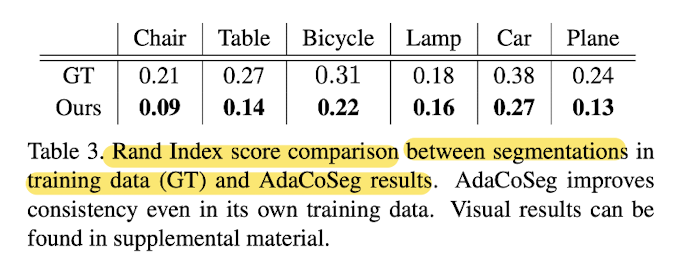
• Tab3. shows that AdaCoSeg can even
  improve the segmentation quality of its own training data.

• Fig9. demonstrates a significant improvement
  by paper's co-seg over the noisy training data.

🌲 Limitations

• Paper reiterate that online co-seg network does not generalize to new inputs, which is by design:
  the network weights are derived to minimize the loss function for the current input set
  and reomputed for each new set.

• AdaCoSeg is not trained end-to-end,
  while an end-to-end deep co-seg netowork is desirable

• Capable of handling some intra-category variations,
  but learning parts and their feature descriptions
  with all categories mixed together is more challenging.

• Learned network weights cannot be continuously updated as new shape come tin.