Deep Functional Dictionaries: Learning Consistent Semantic Structures on 3D Models from Functions
ML For 3D Data
🚀 Motivations
-
3D semantic attributes
(such as segmentation masks, geometric features, keypoints, and materials)
can be encoded as per-point probe functions
on 3D geometries.
✅ probe functions: per-point functions defined on the shape surface -
Given a collection of related 3D shapes,
this paper considers
"how to jointly analyze such probe functions over different shapes", and
"how to discover common latent structures using a neural network"
even absence of any correspondence information
🛩️ Approach
-
Instead of a two-stage procedure
to first build independent functional spaces
and then relate them through correspondences(functional or traditional),
🔽
This paper proposes a correspondence free framework
that directly learns consistent bases across a shape collection
that reflect the shared structure of the set of probe functions. -
Paper produces a compact encoding
for meaningful functions over a collection of related 3D shapes
by learning a small functional basis for each shape
using neural netwroks. -
Set of functional bases of each shape,
a.k.a a shape-dependent dictionary,
is computed as a set of functions on a point cloud
representing the underlying geometry
(a functional set whose span will include probe functions on that space.) -
Training is accomplished in a very simple manner
by giving the network sequences of pairs
consisting of a shape geometry(as point clouds)
and a semantic probe function on that geometry
(that should be in the associated basis span). -
The NN will maximize its representational capacity
by learning consistent bases
that reflect this shared functional structure,
leading in turn to consistent sparse function encodings. -
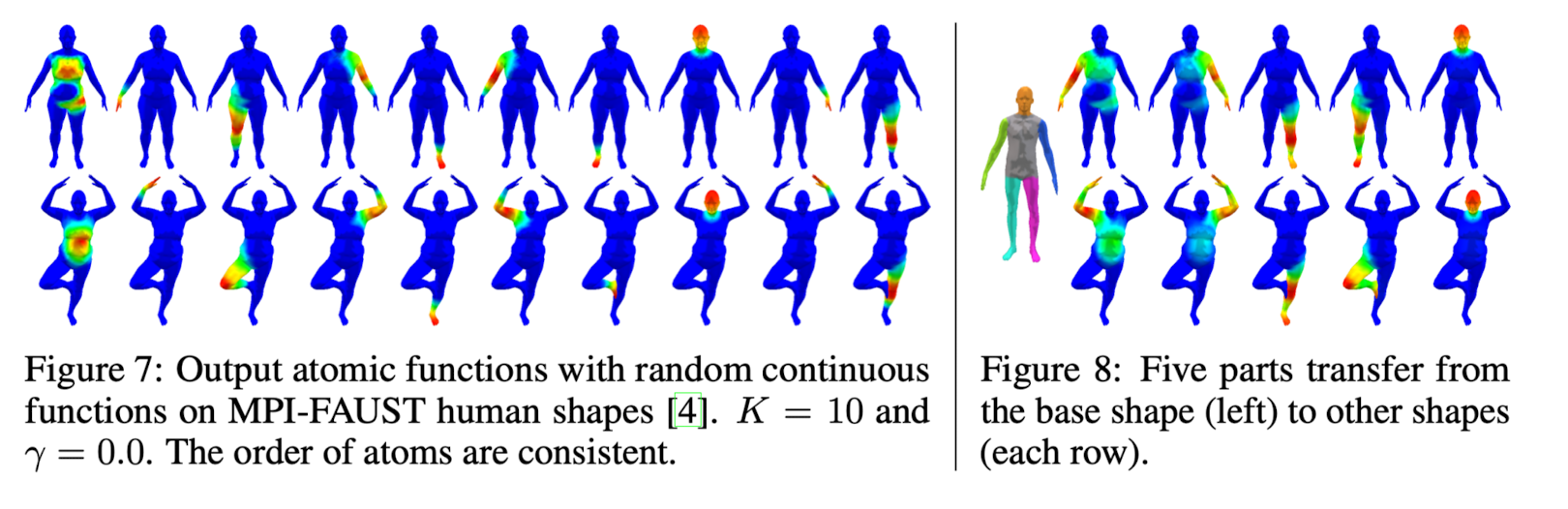
Thus, consistent functional bases emerge from the network without explicit supervision.
🔑 Key Contributions
- Model does not require precomputed basis functions.
(Typical bases such as Laplacian (on graphs) or Laplace-Beltrami (on mesh surfaces) eigen functions need extra preprocessing time.)
Thus, be able to avoid the overhead of preprocessing by predicting dictionaries
while also synchronizing them simultaneously.
- Model does not require precomputed basis functions.
- Paper's dictionaries are application driven,
so each atom of the dictionary iteself can attain a semantic meaning
associated with small scale geometry, such as a small part or a keypoint.
(While LB eigenfunctions are only suitable for approximating continuous and smooth functions due to basis truncation)
- Paper's dictionaries are application driven,
- Model's NN becomes synchronizer,
without any explicit canonical bases
(While previous works define canonical bases,
and the synchronization is achieved from the mapping
between each individual set of bases and canonical bases)
- Model's NN becomes synchronizer,
- Paper obtains a data-dependent dictionary
(Compared with calssical dictionary learning works
that assume a universal dictionary for all data instances)
that allows non-linear distortion of atoms
but still preserves consistency,
which endows additional modeling power
without sacrificng model interpretability.
- Paper obtains a data-dependent dictionary
👩🏻⚖️ Problem Statement
-
Given a collection of shapes {Xi}, each of which has
a sample function of specific semantic meaning {fi}
(e.g. indicator of a subset of semantic parts or keypoints),
🔽
we consider the problem of
1) sharing the semantic information across the shapes, and
2) predicting a functional dictionary A(X;Θ) for each shape
that linearly spans all plausible semantic functions on the shape (Θ: NN weights) -
Assume that shape is given as n points sampled on its surface,
a function f is represented with a vector in ℝ^n (a scalar per point),
and atoms of the dictionary are represented as columns of a matrix A(X;Θ) ∈ ℝ^(n x k),
(k: sufficently large number for the size of dictionary) -
Note that the column space of A(X;Θ)
can include any function f
if it has all Dirac delta functions of all points as columns. -
Paper aims at finding a much lower-dimensional vector space
that also contains all plausible semantic functions. -
Also, force the columns of A(X;Θ)
to encode atomic semantics in applications
such as atomic instances in segmentation,
by adding appropriate constraints.
⭐ Methods
Abstract
-
Paper's network is trained on
point cloud representations of shape geometry
and associated semantic functions on that point cloud. -
These functions express a shared semantic understanding of the shapes
but are not coordinated in any way. -
Network is able to produce a small dictionary of basis functions for each shape,
a dictionary whose span includes
the semantic functions provided for that shape. -
Even though our shapes have
independent discretizations and no functional correspondences are provided,
network can generate latent bases,
in a consistent order,
that reflect the shared semantic structure among the shapes.
Deep Functional Dictionary Learning Framework
General Framework
NN input: pairs of a shape X
including n points and a function f ∈ ℝ^n
NN output: matrix A(X;Θ) ∈ ℝ^(n x k)
as a dictionary of functions on the shape.
Proposed Loss function:
loss function is designed for minimizing both
1) projection error from the input function f
to the vector space A(X;Θ)
2) number of atoms in the dictionary matrix.
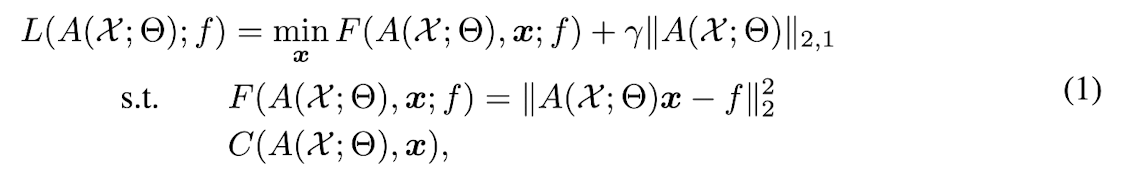
-
where x ∈ ℝ^k : linear combination weight vector,
γ: weight for a regularization
F(A(X;Θ)): function that measures the projection error,
l2,1-norm : regularizer inducing structured sparsity,
encouraging more columns to be zero vectors.
C(A(X;Θ), x): set of constraints on both A(X;Θ) and x
depending on the applications.
For example, when the input function in an indicator(binary function,
we constrain all elements in both A(X;Θ) and x
to be in [0, 1] range -
Note paper's loss minimization is a min-min optimzation problem
🍇 inner minimization (embedded in loss function in Eq.1)
optimizes the reconstruction coefficients
based on the shape dependent dictionary predicted by the network.
🍊 outer minimization,
minimizes our loss function,
updates the NN weights to predict a best shape dependent dictionary. -
Nested minimization generally does not have an analytic solution due to the constraint on x.
Thus, impossible to directly compute the gradient of L(A(X;Θ); f) without x.
🔽
solve this by an alternating minimization scheme as describe in Alogrithm.1

In a single gradient descent step,
first minimize F(A(X;Θ); f) over x with the current A(X;Θ),
and then compute the gradient of L(A(X;Θ); f) while
fixing x.
Adaptation in Weakly-supervised Co-segmentation
-
Some constraints for both A(X;Θ) and x
can be induced from the assumptions of
input function f and the properties of the dictionary atoms. -
In the segmentation problem, we take an indicator function of a set of segments as an input,
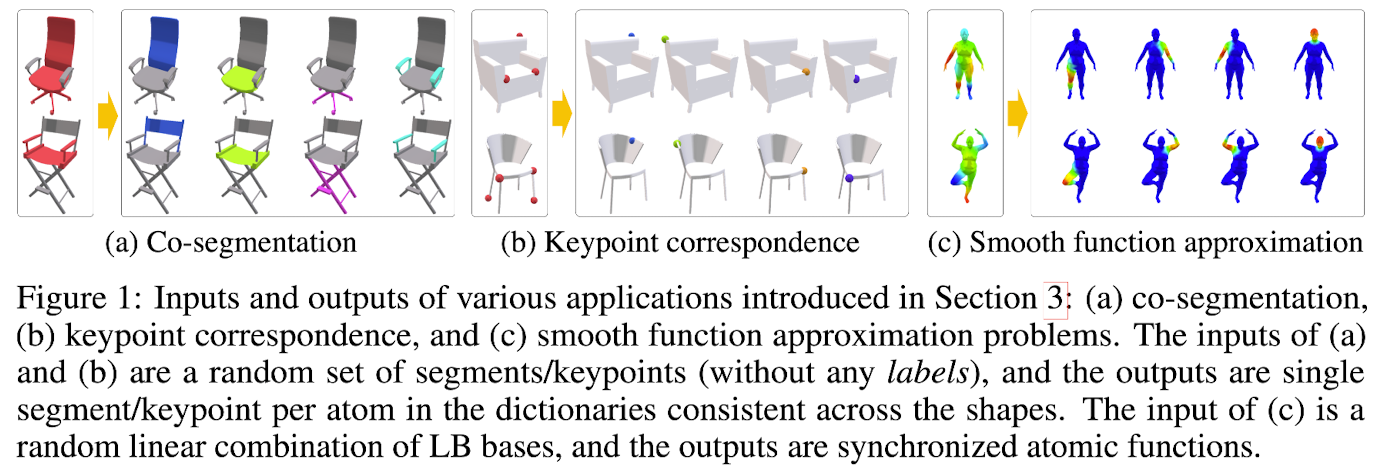
and we desire that each atom in the output dictionary indicates an atomic part Figure 1 (a).
This, we restrict both A(X;Θ) and x to have values in the [0 ,1] range.
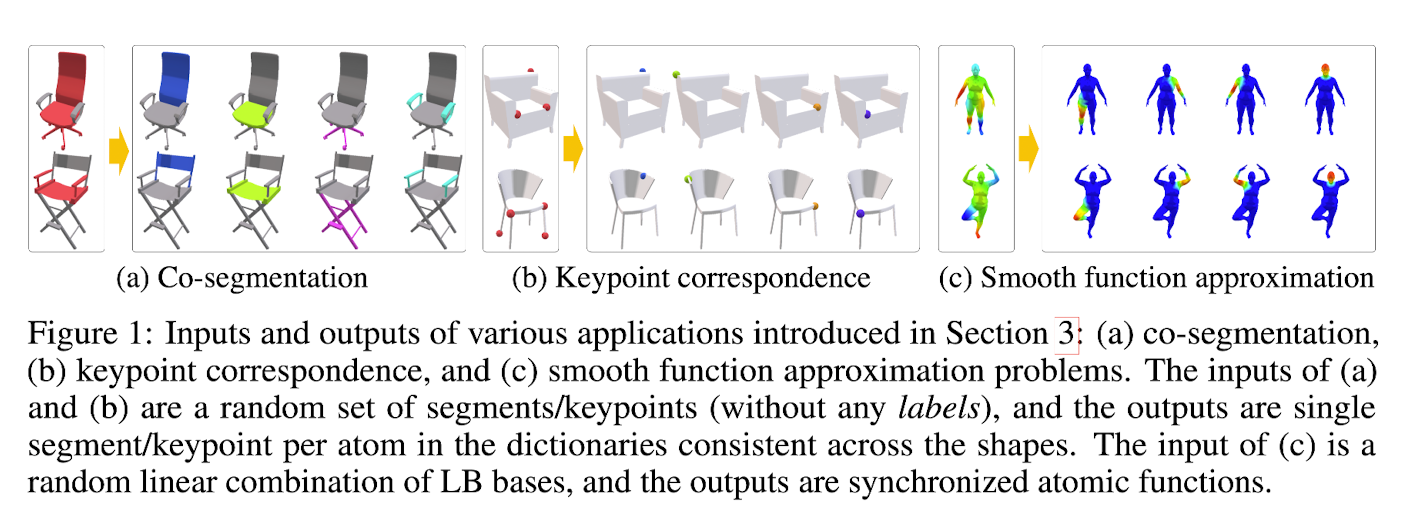
-
Atomic parts in the dictionary must partition the shape,
meaning that each point must be assigned to one and only one atom.
🔽 Thus, we add sum-to-one constraint for every row of A(X;Θ) -
The set of constraints for the segmentation problem is defined as follows:
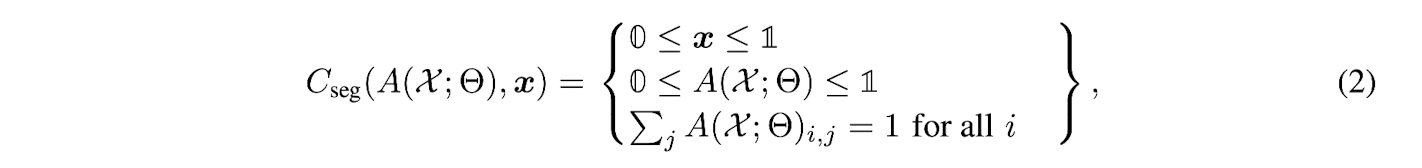
where A(X;Θ)i,j : (i, j)-th element of matrix A(X;Θ)
0 and 1 : vectors/matrices with an appropriate size
➡️
The first constraint on x is incorporated in solving the inner minimization problem,
second and third constraints on A(X;Θ) can simply be implemented
by using softmax activation at the last layer of the network.
Adaptation in Weakly-supervised Keypoint Correspondence Estimation
-
Similarly with the segmentation problem,
the input function in the keypoint correspondence problem is also
an indicator finction of a set of points (Fig 1(b))
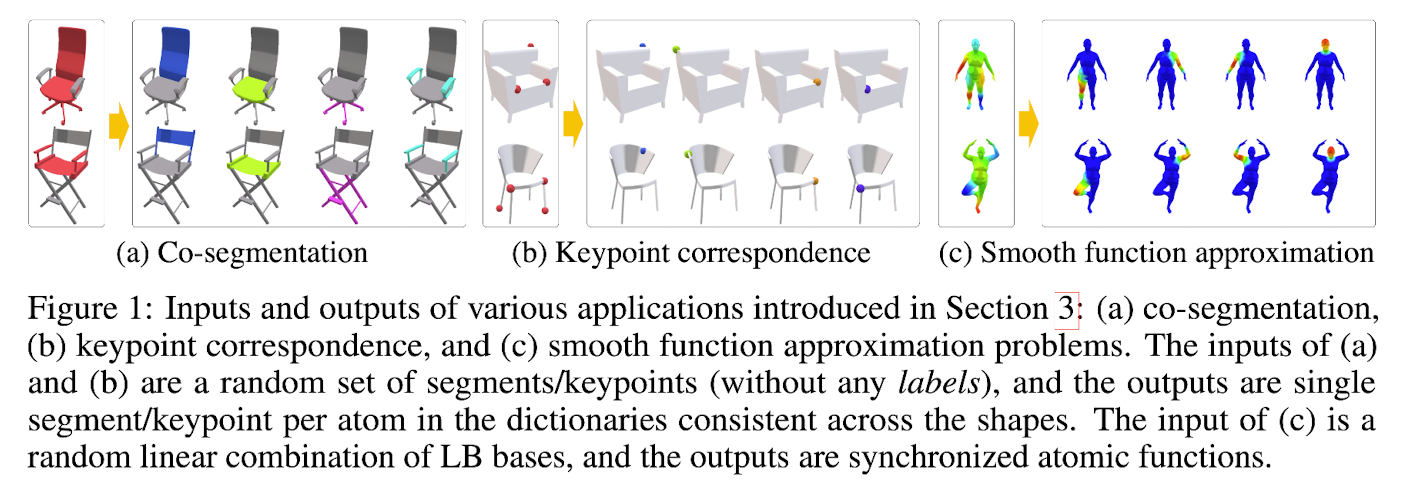
-
Thus, use the same [0,1] range constraint for both A(X;Θ) and x.
-
Each atom needs to represent a single point,
and thus we add sum-to-one constraint
for every column of A(X;Θ):
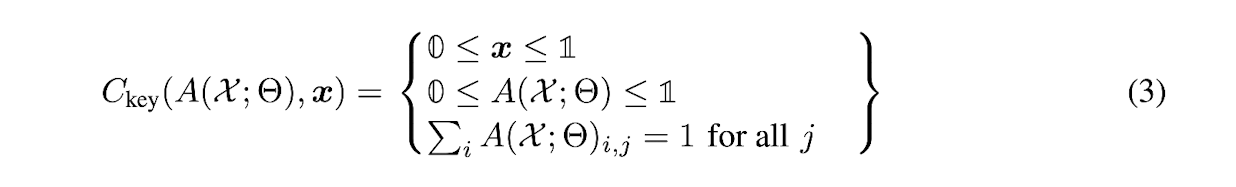
-
For robustness, a distance function from the keypoints can be used a input
instead of the binary indicator function. -
Paper uses a normalized Gaussian-weighed distance function g in experiment:

Adaptation in Smooth Function Approximation and Mapping
- For predicting atomic functions
whose linear combination can approximate any smooth function,
we generate the input function by
taking a random linear combination of LB bases functions (Fig 1(c))
- Also, use a unit vector constraint for each atom of the dictionary:
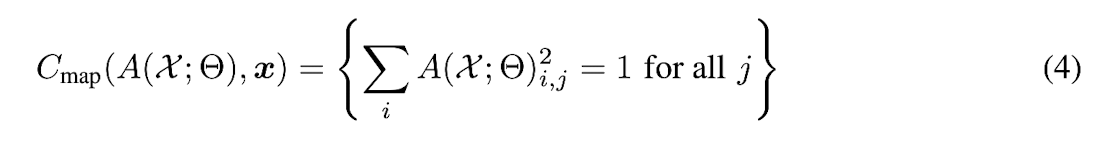
👨🏻🔬 Experimental Results
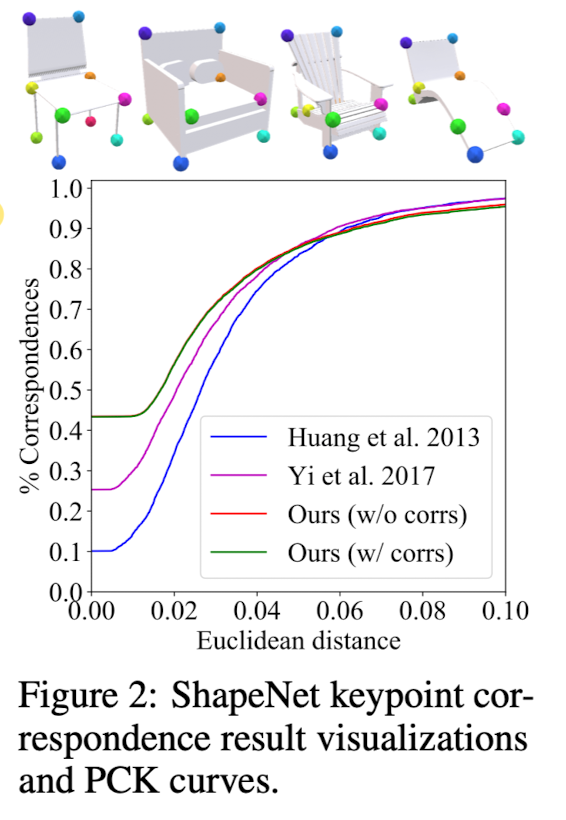
ShapeNet Keypoint Correspondence
red line: best one-to-one correspondences between GT and predicted keypoints for each shape
green line: correspondence between GT labels and atom indices for all shapes
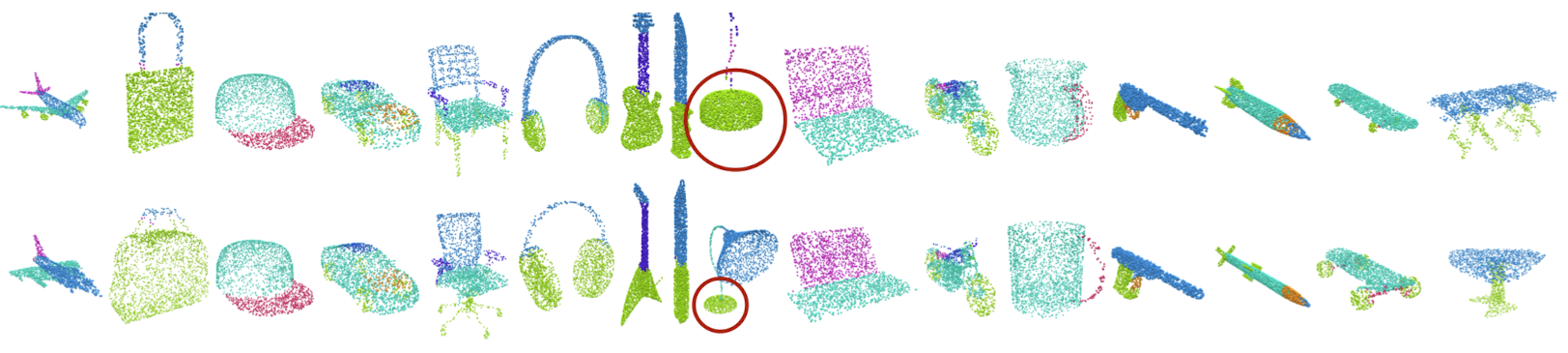
ShapeNet Semantic Part Segmentation
S3DIS Instance Segmentation


MPI-FAUST Human Shape Bases Synchronization