CSG-Stump: A Learning Friendly CSG-Like Representation for Interpretable Shape Parsing
ML For 3D Data
🚀 Motivations
-
Generating an interpretable and compat
representation of 3D shapes from point cloud
is an important and challenging problem. -
CSG models a shape
by iteratively performing Boolean operations
on simple parametric primitives,
usually followed by a binary tree.
➡️ Thus, CSG is an ideal model for providing
compac representaion, high interpretability and editability. -
However, Binary CSG-Tree structure has two challenges:
1) difficult to define a CSG-Tree
with a fixed dimension formulation
2) iterative nature of CSG-Tree construction
cannot be formulated as matrix opearions
and long suequence optimization suufers vanishing gradients. -
Previous Method
CSG-Net: employed an RNN tree structure prediction
🔥 However, requires expensive annotations with expert knowledge
BSP-Net & CVX-Net: leverage a set of parametric hyperplanes
to represent a shape,
🔥 However, abundant hyperplanes are needed to approximate curved surface
UCSG-Net: CSG-Layer to generate highly interpretable shapes by a multi-layer CSG-Tree iteratively,
🔥 only a few layers can be supported because of the optimization difficulty,
which greatly restricts the diversity and representation capability.
-
✅ This paper presents CSG-Stump Net,
an unsupervised end-to-end network
for learning shapes from point clouds
&
discovering the underlying constituent modeling primitives and operations as well. -
➡️ CSG-Stump is proven to be equivalent to CSG in terms of representation,
therefore inheriting the interpretable, compact and editable nature of CSG
while freeing from CSG's complex tree structures -
➡️ CSG-Stump has a simple and regular structure,
allowing neural networks to give outputs of a constant dimensionality,
which makes itself deep-learning friendly.
🔑 Key Contributions
-
Paper proposes CSG-Stump, a three-layer reformulation of the classic CSG- Tree
for a better interpretable, trainable and learning friendly representation,
and provide theoretical proof of the equivalence between CSG-Stump and CSG-Tree -
Paper demonstrates that CSG-Sump is highly compatible with deep larning.
Whith its help, even a simple unsupervised end-to-end network
can perform dynamic shape abstraction. -
Extensive experiments are conducted
to show that CSG-Stump achives SOTA results
while allowing further edits and manipulation.
⭐ Methods
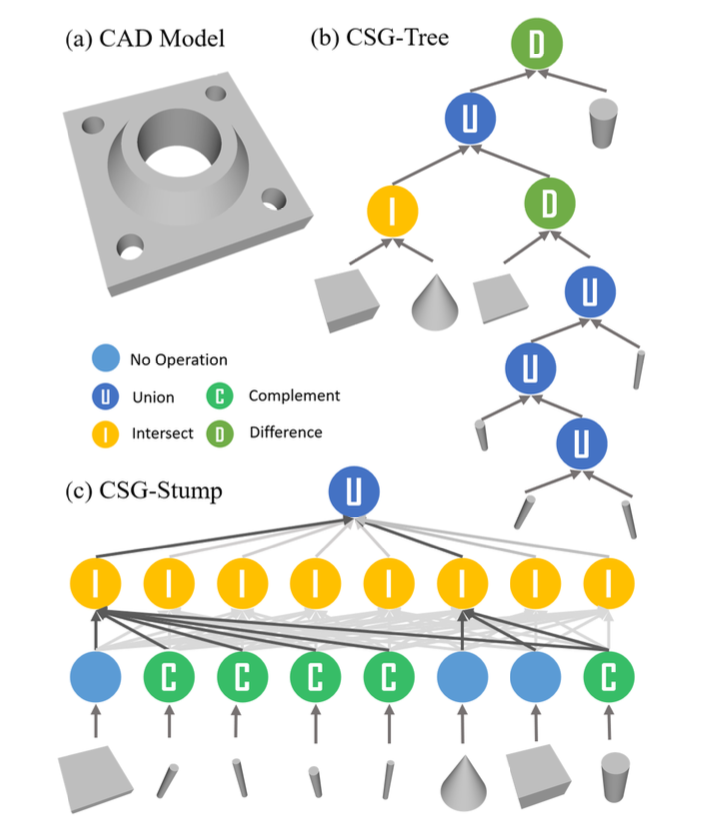
CSG-Stump: 3-layer tree representation for 3D shapes
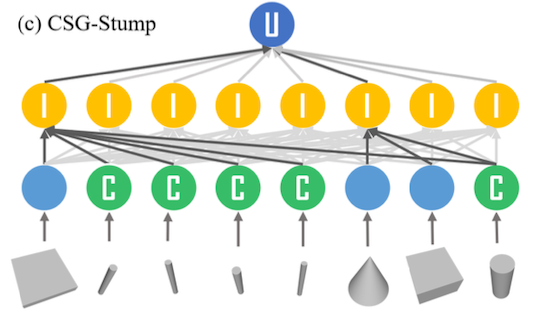
-
CSG-Stump has 3 level structure, consisting of
complement layer at the bottom,
intersection layer in the middle,
and union layer at the top. -
For each layer in the CSG-Stump,
introduce a coneection matrix
to encode the information for its node. -
In this way, CSG-Stump represents a shape
by a set of primitive shapes and three connection matrices. -
- Paper defines a shape O
by an occupancy function O(x): ℝ^3 -> {0, 1} as follows:
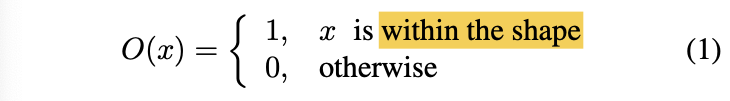
- Paper defines a shape O
1) complement layer at the bottom
-
nodes correspond to the primitive one-to-one.
-
nodes store wheter the complement operations is performed
on their corresponding primitives. -
1 x K matrix Wc ∈ {0, 1} ^ K
(K: number of the primitives) -
Wc[1, i] = 0 or 1 encodes whether
the shape of primitive i or its complement
is used for node i
of complement layer. -
Function Represention:
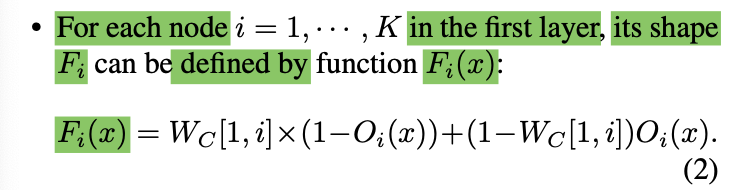
2) intersection layer in the middle
-
nodes record which shapes generated in the bottom layer
are selected for the intersection layer -
K x C matrix WI ∈ {0, 1} ^ (K x C)
(C: number of nodes in the intersection layer) -
If WI[j, i] = 1,
shape from node j in the complemnt layer
is selected for the intersection in node i
of intersection layer. -
Function Represention:

3) union layer at the top.
-
node records which shapes generated in the intersection layer
are selected for the union operation. -
C X 1 matrix WU WI ∈ {0, 1} ^ C
-
If WU[j, 1] = 1,
shape from node j in the intersection layer
is selected for the union operation
at top layer. -
Function Represention:

Advantage over CSG-Tree
-
CSG-Tree representation is orgainzed as a binary tree
with many layers,
which makes the prediction of primitives and Boolean operations
a challenging iterative process. -
Particulary, working with a long sequence not only causes
problems in gradient feedback
but also is sensitive to the order of
primitives and Boolean operations. -
In contrast, CSG-Stump has
a fixed type of Boolean operations at each layer
and
only requires determining 3 binary connection matrices,
➡️ which makes CSG-Stump learning friendly
Binary Programming Formulation
-
Input: shape given by a point cloud X = {xi} ^ N
consisting of a list of 3D points xi -
And we want to reconstruct a CSG-like representation for the shape.
-
First obtain the target shape occupancy Oi
and detect the underlying primitives. -
Then reconstructing a CSG-Stump reprsentation
is simplified to finding the three connection matrices.
✅ This can be formulated as a Binary programming problem. -
Let
Ok(i): occpancy value of testing point i
for primitive k
&
T(i): estimated occupacny of point i -
The connection matrices Wc, WI, WU
for the selection process of CSG-Stump
are the solution of the following minimization problem:
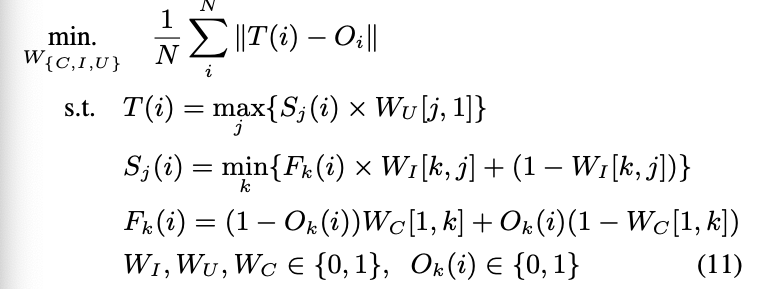
CSG-StumpNet
-
When a relatively large number of primitives are required
to represent a shape,
Binary programming typically fails
to obatin an optimal solution in polynomial time
due to the combinational nature of the problem. -
Therefore, paper proposes a learning-based approah
by designing CSG-StumpNet
to jointly detect primitives
and estimate CSG-Stump connections. -
Architecture
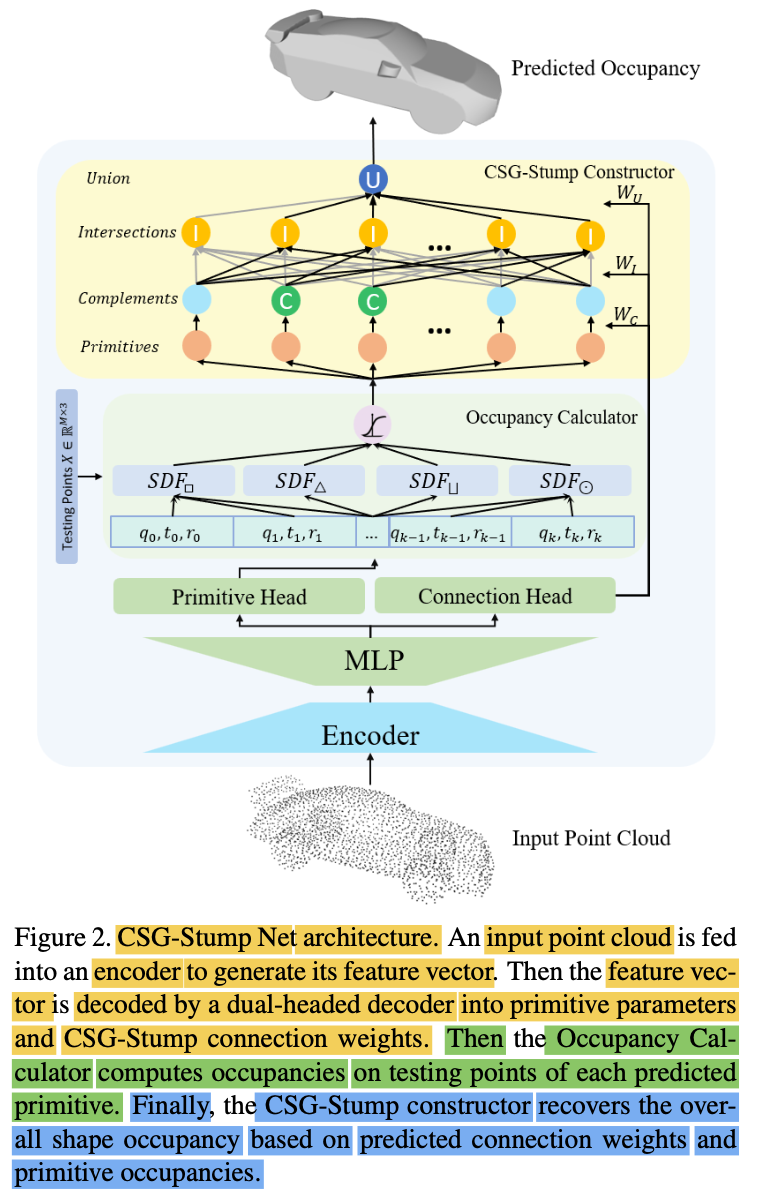
-
1️⃣ First encodes a point cloud into a latent feature (encoder: DGCNN in the paper)
2️⃣ Then, decodes it into primitives
and connections via the 'primitive head' & the 'connection head' respectively,
3️⃣ Follwed by occupancy calculation and
CSG-Stump construction
Dual-Headed Decoder
-
Enhance the latent feature
with 3 FCL ([512, 1024, 2048]) -
and then use 2 differnt heads
to further decode the feature into primitive paramters
and connection matrices.
Primitive Head
-
decodes latent features into a set of K parametirc primitives
where each parametric primitive is represented by
intrinsic and extrinsic parameters. -
Intinsic parameters q
model the shape of the primitive,
such as sphere radius and box dimenstions -
Extrinsic parametrs
model the global shape transformation
composed of a translation vector t ∈ ℝ^3
& rotation vector in quaternion form r ∈ ℝ^4. -
Paper selects 4 typical types of
parametric primitives,
i.e, box, sphere, cylinder and cone,
as the primitive set,
which are standard primitives in CSG representation. -
For simplicity, paper predicts equal numers of
K primitives for each type.
CSG-Stump Connection Head
-
Leverages binary matrices
to represent Boolean operations among different primitives. -
Paper uses 3 dedicated single layer perceptrons
to decode the encoded features
into the connection matrices Wc, WI and WU. -
As binary value is not differentiable,
paper relaxes this constraint
by predicting a soft connection weight in [0, 1]
using the Sigmoid Function.
Differentiable Occupancy Calculator
-
To generate primitive's occupancy function
in a differential fashion,
first compute the primitive's SDF
and convert it to occupancy differentially. -
Denoting the corresponding operations
for the extrinsic parameters of a primitive
as translation T and rotation R,
point x in the world coordinate
can be transformed to
point x' in a local primitive coordinate as
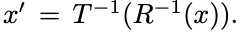
-
Afterward, SDF can be calculated
according to the formulation of differnt primitives. -
SDF is further converted to occupancy
by a sigmoid function Φ:

CSG-Stump Constructor
-
Given the predicted primitives occupancy and connection matrices,
we can finally calculate the occupancy of the overall shape
using the formulations of CSG-Stump -
Note that the complement layer (at the bottom)
can now be written as:
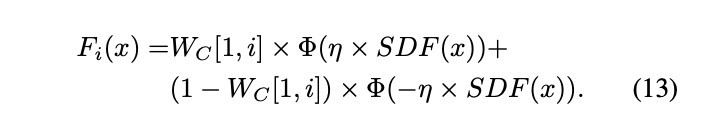
Training and Inference
-
Training
-
Train CSG-StumpNet in an unsupervised manner.
-
CSG-StumpNet learns to predict a CSG-Stump
with primitives and their connections
w.o. explicit GT. -
Instead, supervision signal is quantified
by the reconstruction loss
betweem the predicted and GT occupancy. -
Sample testing points X ∈ ℝ ^ (Nx3)
from the shape bounding box
and measutre the discrepancy
between GT occupancy O* and the predicted occupancy O hat
as follows:
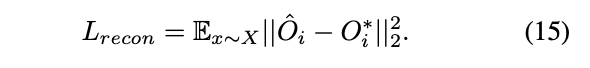
-
author observes that testing points far away from a primitive surface
have gradient close to zero,
thus stalling the training process.
➡️ To address this issue,
paper proposes a primitive loss
to pull each primitive surface to its closes test point,
which prevents the gradient from vanishing.
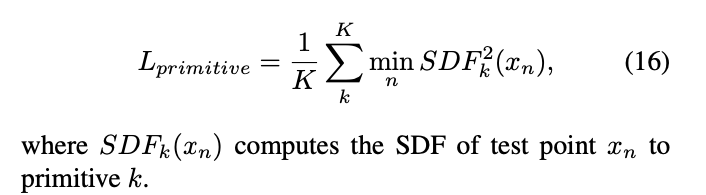
-
Finally, the overall objective can be defined as
ths joint loss of the above two terms:
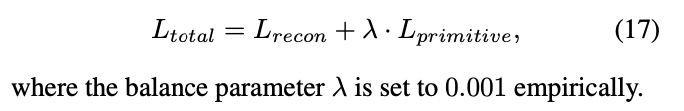
-
Inference
-
Follow the same procedure as training
except that binarize predicted connection matrices
with a threshold 0.5
to fulfull the binary constrain
and generate an interpretable and editable CSG-Stump representation.
👨🏻🔬 Experimental Results
CSG-Stump Evaluation
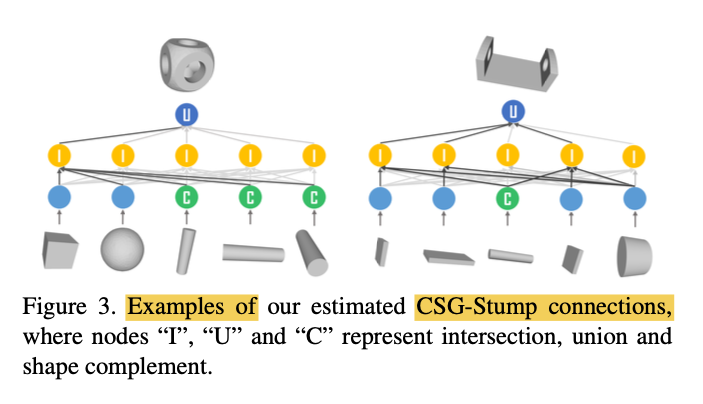
-
Solver can find the optimal solution
and converge to zero objective loss within a minute
for the toy dataset. -
However, solver fails to find an optimal solution
within a reasonalbe time limi
when paper tset on some complex shapes from ShapeNet Dataset. -
This is likely because of the combinatorial complexity of the optimization problem
and noisy input shapes. -
Therefore, paper proposes a deep learning based CSG-StumpNet solution.
CSG-StumpNet Evaluation
-
Dataset: ShapeNet
-
Randomly sample 2048 points on a shape surface
as an input point cloud
&
generate N = 2048 points in the shape boundinng box
as testing points -
In experiment, paper founds that
randomly sampled testing points
tend to miss reconstructing this structures.
Therefore, uses a balanced sampling strategy(1:1 for inside and outside points) during training.
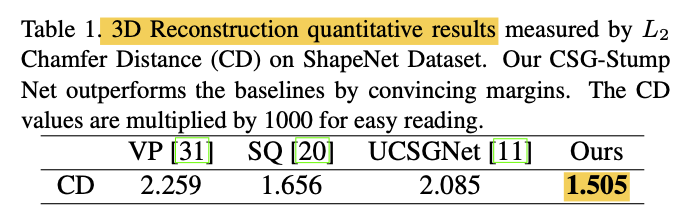
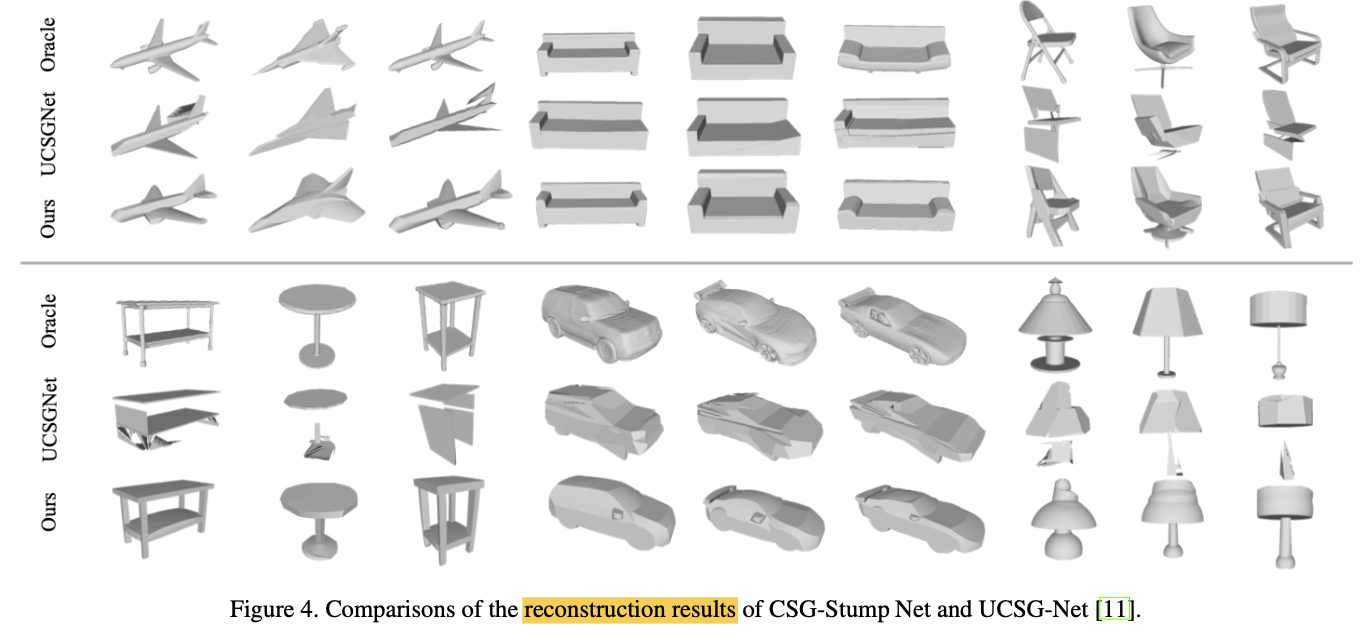
Comparison with SOTA models
Performance on Compactnetss
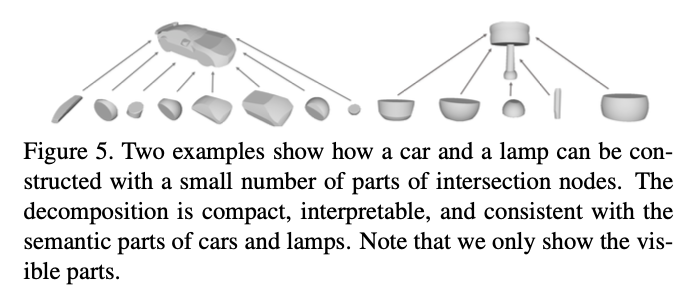
- Only a small subset of intersectionnodes
is used to construct the final shape,
which suggest that the obtained structure is compact.
Ablation on Number of Primitives
-

-
Allowing more primitives improves the performance.
Ablation on the Number of Intersection Nodes.

- More intersection nodes lead to better results
but at the cost of reducing compactness
and increasing network complexity.
✅ Conclusion
-
Paper presented CSG-Stump,
a 3-level CSG-like representation for 3D shapes. -
While it inherits the compact, interpretable and editable nature of CSG-Tree,
It is learning friendly and has high representation capability. -
Based on CSG-Stump, paper designs CSG-StumpNet,
which can be trained end-to-end in an unsupervised manner. -
Paper demonstrates that CSG-Stump outperforms existing methods by a significant margin.