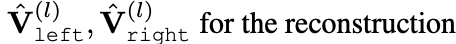UCSG-NET - Unsupervised Discovering of Constructive Solid Geometry Tree

YEOM JINSEOP·2023년 9월 12일

ML For 3D Data

목록 보기

25/27

🚀 Motivations

Methods based on SDF struggle to reconstruct non-convex shapes.
One remedy is to incorporate a CSG(constructive solid geometry) framework
that represents a shape
as a decomposition into primitives.
It allows to embody a 3D shape of high complexity and non-convexity
with a simple tree representation of Boolean operations.
🤔 Neverthless, existing approaches are supervised
and require the entire CSG parse tree
that is given upfront during the training process.

1️⃣ Existing methods for representing meshes,
such as BSP-NET and CVXNET's drawbacks
1) generating mesh from predicted planes
requires an additional post-processing step.
2) assume any object can be decomposed into a union of convex primitives
➡️ While holding, it requires many such primitives
to represent concave shapes.
3) Decoding process is difficult to explain
and modified with some external exprt knowledge

2️⃣ CSG-NET utilize CSG parse tree
to represent 3D shape construction process
➡️ require expensive supervision
that assumes assigned CSG parse tree
for each example given during training.

✅ Paper proposes a model UCSG-NET
for representing 3D meshes
capable of learning CSG parse trees
in an unsupervised manner
Suggested model predicts parameters of primitive
and binarize their SDF representation
through differentiable indicator function.
Achieve goals by introducing CSG Layers
capable of learning explainable Boolean operations
for pairs primitives.

🔑 Key Contributions

First method able to predict CSG tree
without any supervision.
Achieve SOTA results on the 2D reconstruction task
comparing to CSG-NET trained in a supervised manner.
Predictions of method are fully interpretable
and can aid in CAD applications.
Define and describe a novel formulation of
constructive solid geometry operations
for occupancy value representations
for 2D and 3D data.

⭐ Methods

Overview

End-to-end neural network model
that predicts parameters of simple geometric primitives
and their constructive solud geometry composition
to reconsturct a given object.
User can predict the CSG parse tree
that can be further passed to an external rendering SW
in order to reconstruc the shape
To achieve this, model predicts primitive shapes
in SDF representation.
Then, converts them into a occupancy values O
taking 1 : if a point in the space is inside the shape
0: outside the shape.
CSG operations on such a representation
are defined as clipped summations
and differences of binary values.
Model dynamically chooses which operation should be used.
During validation, retrieve the predicted CSG parse tree and shape primitives,
and pass them to the rendering SW.
Thus, we need a single point in 3D space
to infer the structure of the CSG tree.
It is possible since primitive parameters and CSG opeartions
are predicted independently from sampled points.

Constructive Solid Geometry Network

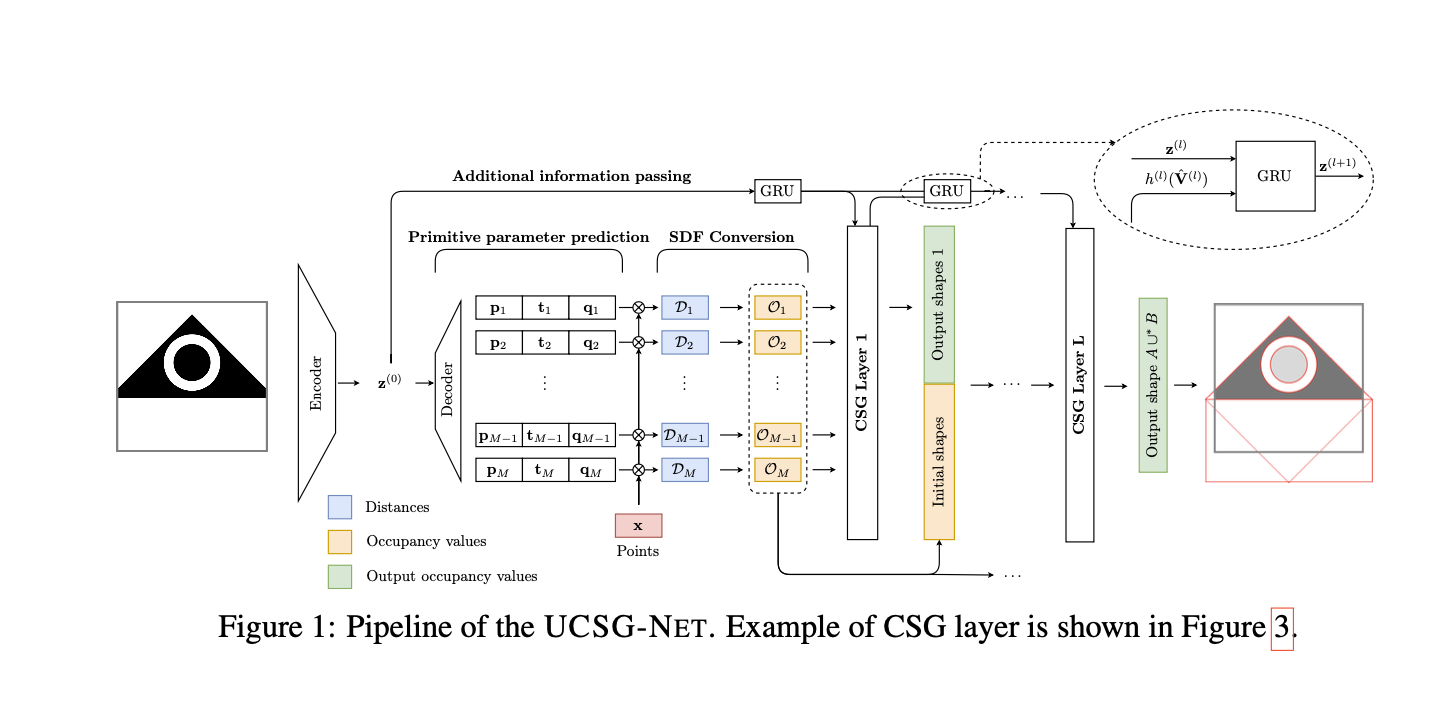
UCSG-NET is composed of

1) encoder

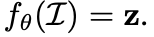
Using an encoder fθ
process input object I
by mapping it into low dimensional vector z
of length d
Depending on the data type,
use either a 2D or 3D CNN as an encoder.
Latent vector is then passed to the
primitive parameter prediction network

2) primitive parameter prediction network

Extract the parameters of the primitives,
given the latent representation of
the input object.
Consists of multiple fully connected layers
interleaved with activation functions.
Last layer predicts parameters of primitives
in the SDF representation.
Consider primitives such as boxes and shpere
that allow us to calcuate signed distance.
Network produces N tuples of

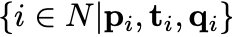
pi ∈ ℝ ^dp: describes vector of parameters of a particular shape (ex. radius of a sphere),
ti ∈ ℝ ^dt: translation of the shape
qi ∈ ℝ ^dq: rotation represented as a quaternion
for 3D shapes and a matrix for 2D shapes.
Further combine k different shapes
to be predicted by using a fully connected layer
for each shape type seaparately,
➡️ thus producing kN = M shapes
and M x(dp + dt+ dq) parameters in total
Once parameters are predicted,
use them to calcuate SDV for sampled points x
from volume of space
that boundaries are normalized to unit square.
For each shape,
that has an analytical equation dist
parameterized by p
that calcuates SD from a point x to its surface,
we obtain

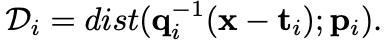
3) SDF to indicator function converter

CSG operations in SDF representation
are often defined as
a combination of min and max functions
on distance values.
one has to apply either
LogSumExp operation as in CVXNET
or standard Softmax function
to obtain differentiable approximation
However, paper casts problem
to predict CSG operations
for occupancy-valued sets
🔥 motivation: these are linear combinations,
hence provide better training stability.
Transfrom signed distance D
to occupancy values O ∈ {0, 1}.
Paper uses parameterized α cliping function
that is learned with the rest of the piple line:

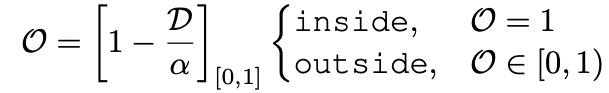
(α: learnable scalar, > 0,
[⋅][0,1] clips values to the given range
O: approximation of occupancy values
O=1 : inside the surface of shape,
O∈[0,1): outside of the shpae)
Graudal leraning of α allows
to distribute gradients to all shpaes
in early stages of training.
(α=1 in paper's experiments
and value is pushed towards 0
by optimizing jointly with the rest of parameters
by adding |α| term to the optimized loss.)

4) constructive solid geometry layers

Predicted sets of occupancy values
and output of the encoder z
are passed to a sequence of L >= 1 CSG layers
that combine shapes using boolean operatos:
union ∪, intersection ∩, difference -*.
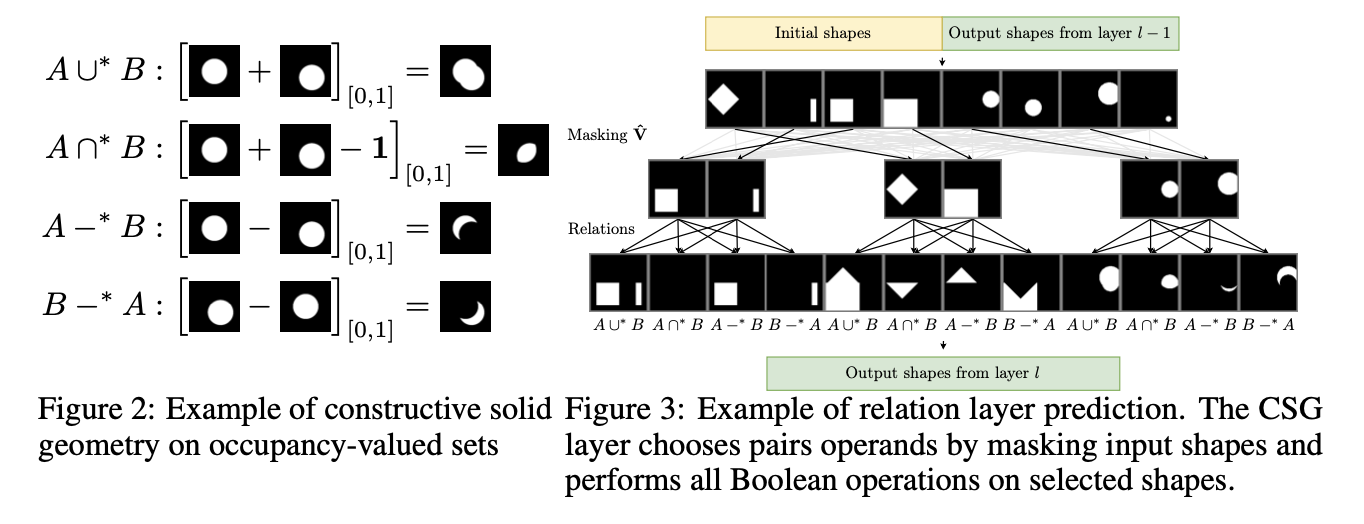
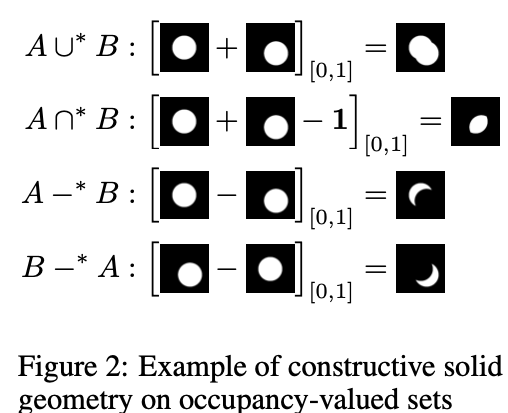
CSG operations for two sets A and B are describe as:
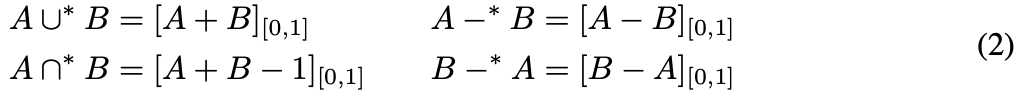
To choose operands A and B,
denoted as left and right operands,
from input shape O(l)
that would compose the output shape in O(l+1),
paper created two learnable matrices
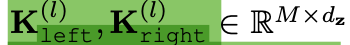
Vectors stored in orws of these matrices
serve as keys for a query z
to select appropriate shapes
for all 4 operations.
Input latent code z
is used as a query
to retrieve the most appropriate operand shapes
for each layer.
Perfrom dot porduct between matrices
K left, K right and z,
and compute softmax along M input shapes.
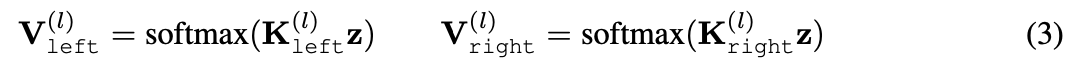
Index of a particular operand
is retrieved using Gumbel-Softmax reparametrization
of the categorical distribution:

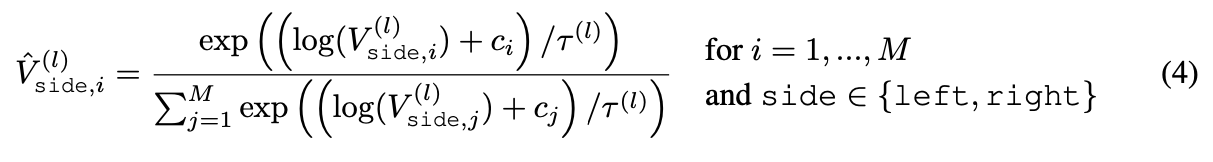
(ci: sample from Gumbel(0,1))
Benefit of reparametrization
1) expectation over the distribution
stays the same
despite changing τ.
2) we can manipulate τ
so for τ -> 0
the distribution degenerates to categorical distribution.
➡️ Hence, a single shape selection replaces
the funzzy sum of all input shapes in that case.
That way, allow the network
to select the most appropriate shape
for the composition during learning
by decreasing τ gradually.
By the end of the learning process,
we can retireve a single shape
to be used for the CSG.
temperature τ is learned jointly
with the rest of the parameters.
Left and right operands are retrieved as:
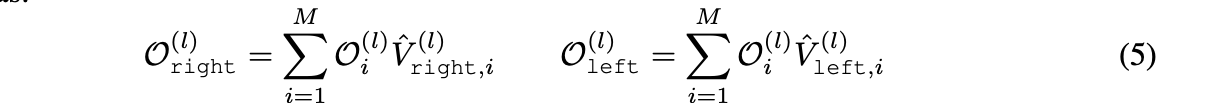
Set of output shapes from the l+1 CSG layer
is obtained by performing
all operations in Eq.2
on selected operands:
By performing these operations manually,
increase the diversity of possible shape combinstaions
and leave to the model
which operations should be used for the reconstruction.

Additional information passing

The info about what is left to reconstruct
changes layer by layer.
Therefore, incorporate it into the latent code
to improve the reconstruction quality
and stabilize training.
Fisrtly, encode

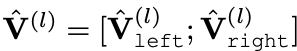
with a neural network h
containing a single hidden layer.
Employ GRU unit
input: latent code z ^(l) and encoded V ^(l)
output: the updated latent code z ^(l+1)
for the next layer.
The hidden state of the GRU unit is learnable.
Initial z ^(0) : output from the encoder.

Interpretability

When α ~= -0,
we obtain occupancy values with Eq.1
Thus, shapes represented as these values
will occupy the same volume
as meshes reconstructed from parameters

This meshes can be visualized and edited explicitly.
To further combine these primitives through CSG operations,
calculate
Then, perform operations

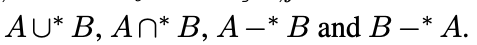
🏋️ Training

Goal is to find compositions of primitives
that minimize the reconstuction error.
Paper employs MSE of predicted occupancy values
with the GT O*
values are calculated for X
which combines points sample from the surface of GT,
and randomly sampled inside a unit cube:
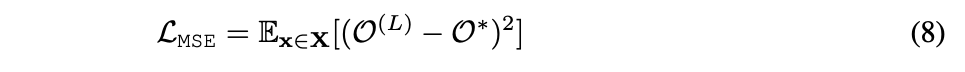
Also ensure that network predicts only positive values of parameters of shapes
since only for such these shapes have analytical descriptions:
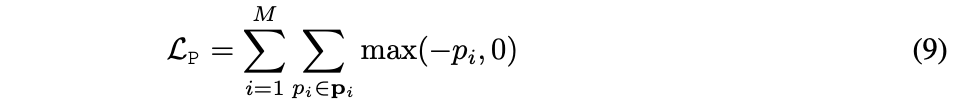
To stop primitives from drifting away
from the center of considered space
in the early stages of tarining,
minimze the clipped square norm of the translation vector.
At ths ame time, allow primitives
to be freely translated inside the space of interest:
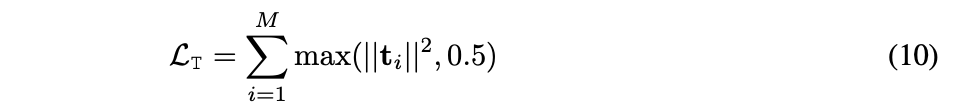
Last component includes minimizing |α|
to perform continuous binarization of distances
into {inside, outside} indicator values.
Goal is to find optimal parameters of model
by minimizing the total loss:

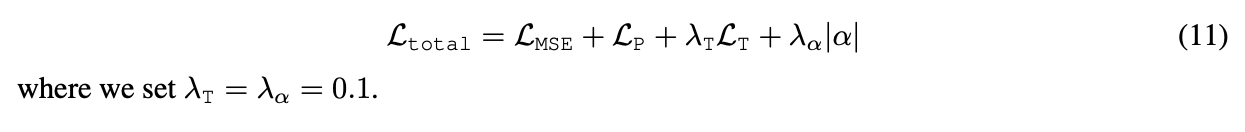
👨🏻‍🔬 Experimental Results

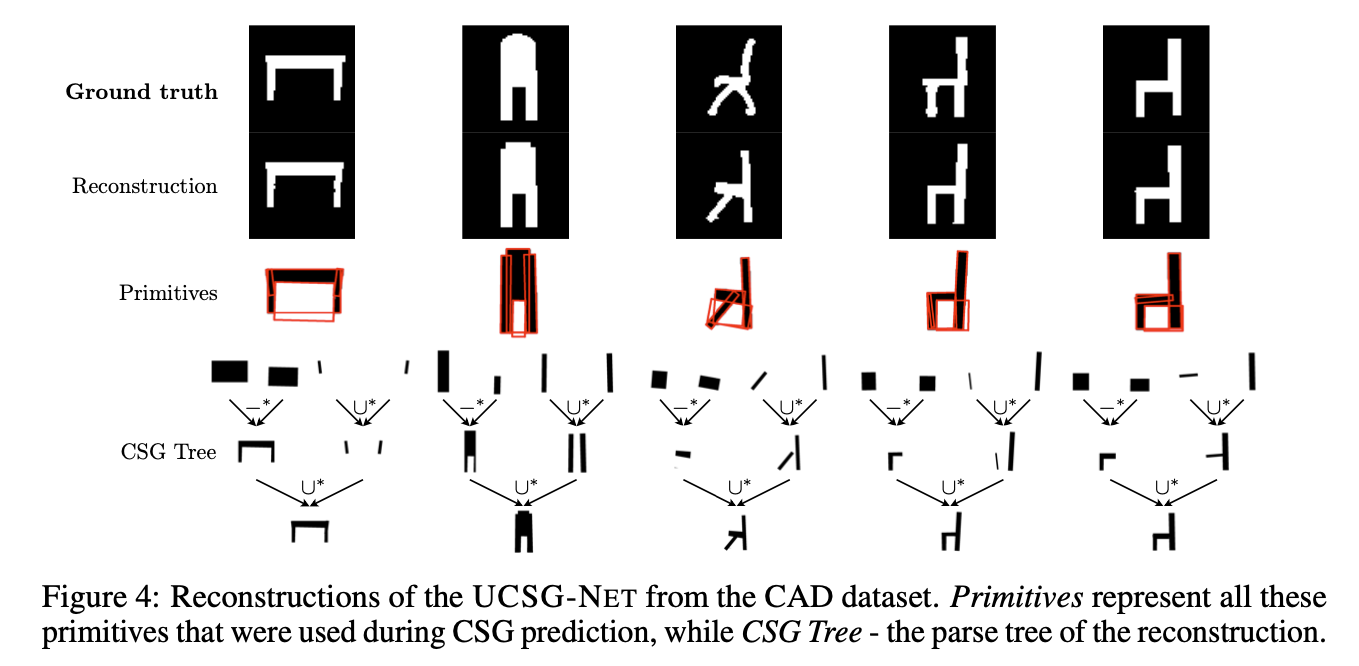
2D Reconstruction

Dataset: CAD dataset
(consisting of 8,000 CAD shapes in 3 categories: chair, desk, and lamps
each shape was rendered to 64 x 64 image.)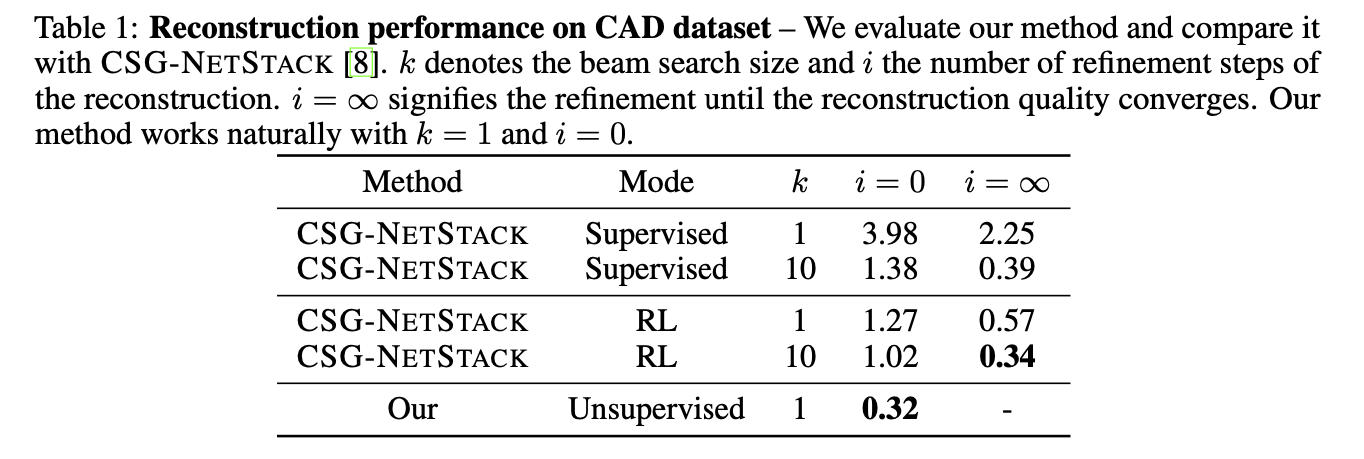

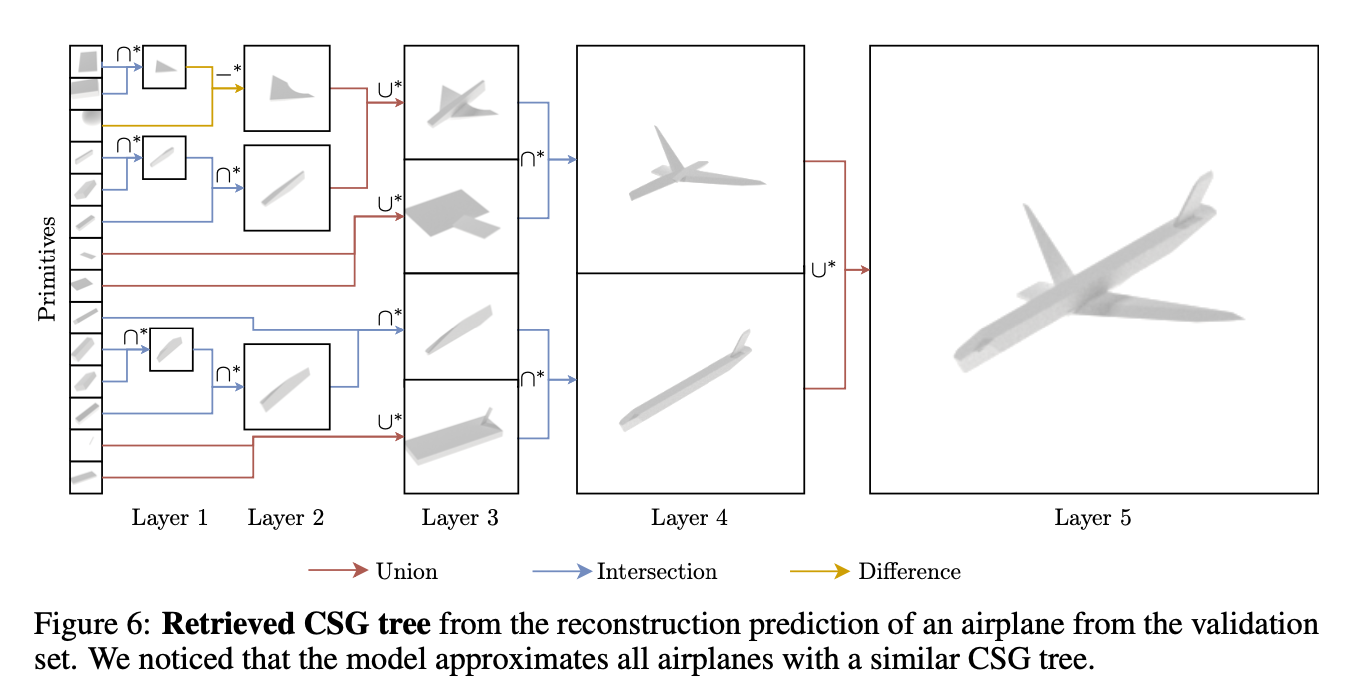
3D Autoencoding

Dataset: ShapeNet
Remaining reerence approaches outperformed paper's model w.r.t CD measure.
It was ainly caused by failed reconstructions of details.
such as engines on wings of airplanes,
to which the metric is sensitive.
➡️ However, paper's ultimate goal was
to provide an effective and interpretable method
to construct a CSG tree
with limited number of primitives.

Accurately reconstucts the main components of a shape
with resembles VP approacg
where outputs can be treated as shape abstractions.

✅ Conclusion

Paper demonstrates UCSG-NET,
an unsupervised method
for discovering constructive solid geometry parse trees
that composes primitives
to reconstruct an input shape.
Method predicts CSG trees
and is able to use different Boolean operations
while maintaining reasonable accuracy of reconstructions.
Inferred CSG trees are usd to form meshes directly,
w.o. need to use explicit reconstruction methods
for implicit representations.