🚀 Motivations
-
Any solid object can be decomposed into
a collection of convex polytopes (in short, convexes). -
This decomposition is fundamental in computer graphics,
where it provides one of the most common ways
to approximate geometry. -
Convex object has the propery of
being simultaneously an explicit and implicit representation:
one can interpre it explicitly as a mesh
derived by computing the vertices of a convex hull,
or implicitly as the collection of half-space constriants or support functions. -
Thier implicit representation makes them
particularly well suited for neural netwrok training,
as they abstract away from the topology of the geometry they need to represent. -
However, at testing time,
convexes can also generate explicit representations - polygonal meshes -
which can then be used in any downstream application. -
✅ Paper introduces a network architecture
to represent a low dimensional family of convexes. -
✅ This family is automatically derived via
an auto-encoding process.
🔑 Key Contributions
-
Proposes a novel representation for geometry
based on primitive decomposition. -
Representation is parsimonious,
as paper approximates geometry
via a small number of convex elements. -
Inspired by recent works,
paper trains pipeline in an unsupervised manner:
predicting the primitive configuration
as well as their parameters
by checking whether the reconstructed geometry matches
the geometry of the target. -
As it is part-basd,
it is naturally locally supported,
and by training on a shape collection,
parts have a semantic association
(i.e. the same element is used to represent the backs of chairs) -
As a convex is defined by
a collection of half-space constraintes,
it can be simultaneously decoded into an explicit(polygonal mesh),
as well as implicit(indicator function) representation. -
Because paper's encoder decomposes geometry into convexes,
it is immediately usable in any application. -
Parts can interact via structuring
to generate smooth blending between parts.
⭐ Methods
Overview
-
Object is represented via an indicator O: ℝ^3 -> [0,1].
-
Surface of the object
is indicated with

-
Indicator function is defined such

-
Given an iniput (e.g. an image, point cloud, or voxel grid)
an encoder estimates the parameters {βk} of template representation
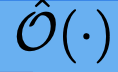
with K primitives. -
Then eavaluate the template
at random sample points x, -
and training loss ensures

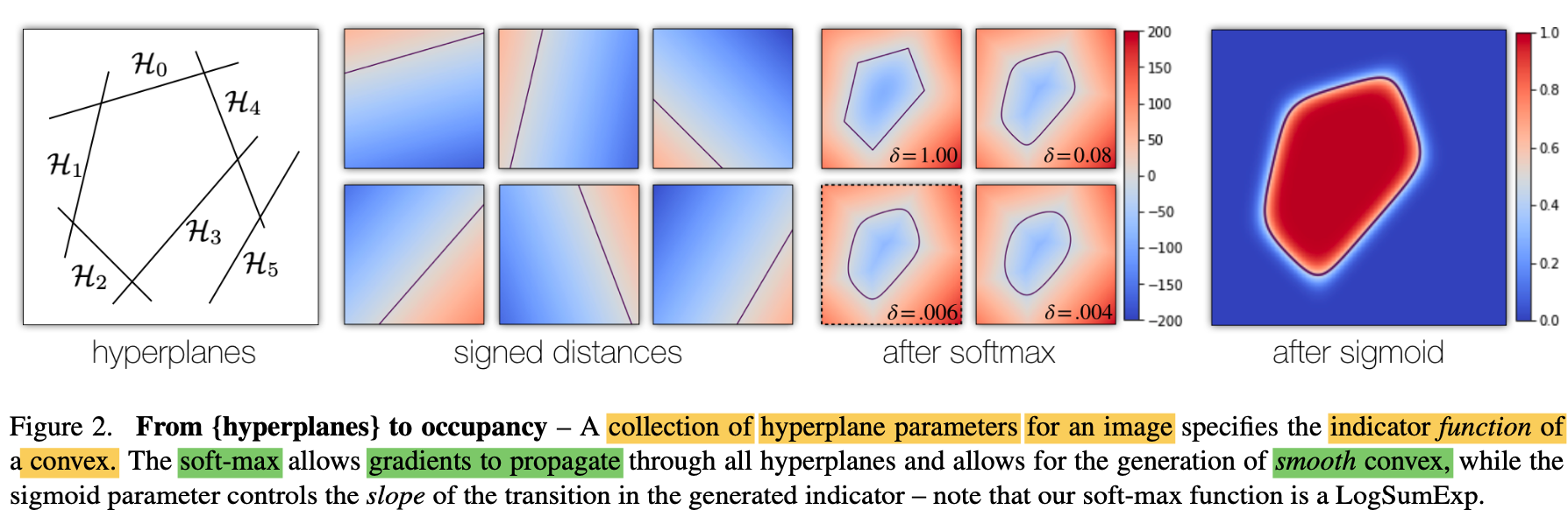
Differentiable convex indicator - Figure 2
-
Define a decoder that
given an collection of half-space constraints
constructes the indicator function of
a single convex object;
(such a function can be evaluated at any point x ∈ ℝ^3 -
Define
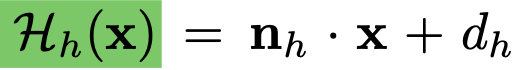
as the signed distance of the point x
from the h-th plane
with normal nh and offset dh. -
Given a sufficiently large number H of half-planes
the SDF of any convex object
can be approximated by taking the max of the SDF of the planes. -
To facilitate gradient learning,
instead of maximum,
paper uses the smooth maximum function LogSumExp
and define the approximate SDF Φ(x):

-
Then, convert the SDF to an indicator function C : ℝ^3 -> [0, 1]:
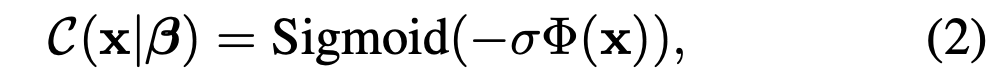
-
Paper denotes
h = {(n, d)} : the collection of hyperplane parameters
β = [h, σ]: overall set of parameters for a convex -
As illustrated in Fig 2,
parameter δ: controls the smoothness of the generated convex,
σ: controls the sharpness of the transition of the indicator function. -
Similar to the smooth maximum function,
the soft classification boundary
created by Sigmoid
facilitaes training.
Convex encoder/decoder - Figure 3
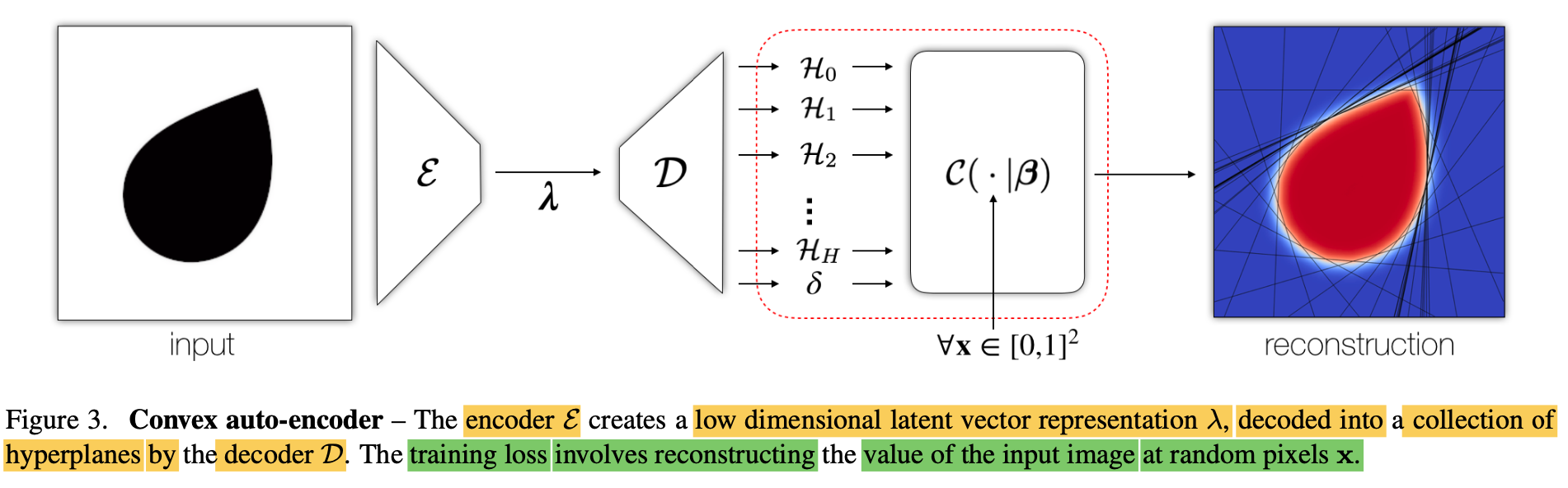
-
A sufficiently large set of hyperplanes
can represent an any convex objects. -
To discover form of correlation between hyperplane paramters,
paper employs an auto-encoder architecture (illustrated in Fig3) -
Given an input,
encoder Ɛ creates a
low dimensional latent vector representation λ
from the input. -
Then, a decoder D derives the
collection of hyperplane parameters. -
While in theory
permuting the H hyperplanes
generate the same convex,
Decoder D correlates a particular hyperplane
with a corresponding orientation.
(This is visible in Fig4, where color-coded different 2D hyperplanes
and indicate their orientation distribution
in a simple 2D auto-encoding task
for a collection of axis-alligned ellipsoids.)
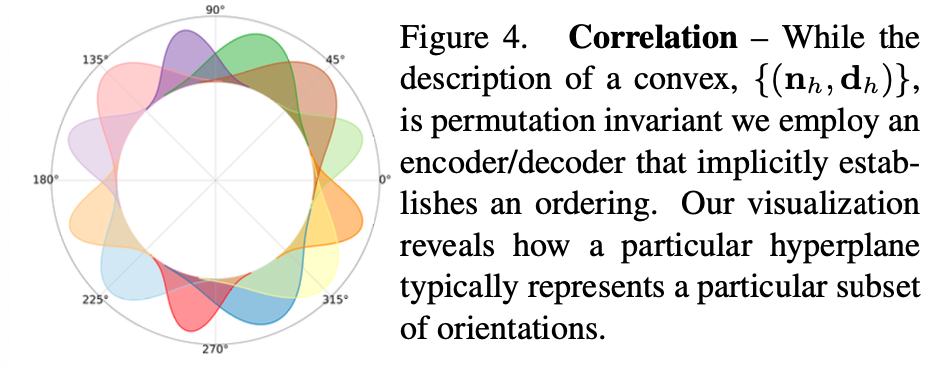
-
As ellipsoid and oriented cuboids are convexes,
paper argues that the architecture in Fig3 allows to
generalize the core geometric primitives
proposed in VP and SIF (vefified in Fig 5)
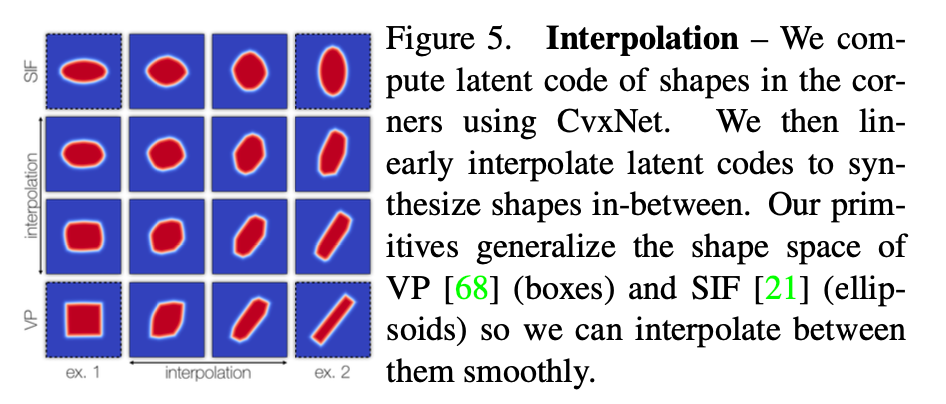
Explicit interpretation - Figure 6
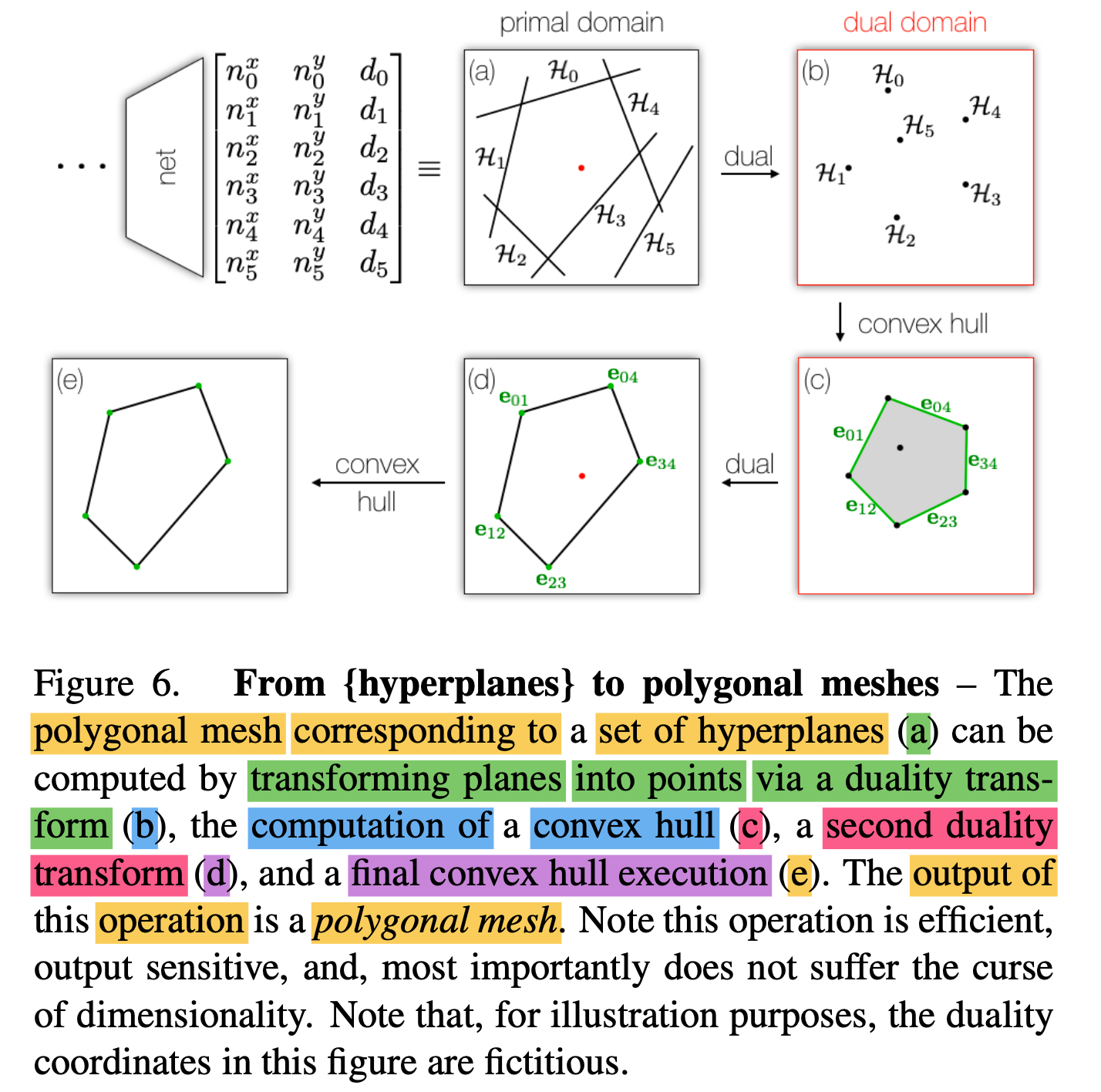
-
Significant difference from other methods
that employ indicator functions
as trainable representations of 3D geometry,
is that convexes generated by paper's network
admit an explicit interpretation
➡️ They can be easily converted into polygonal meshes. -
This is in striking contrast to other papers
where a computationally intensive iso-surfacing operation
need to be executed to extract their surface (e.g. Marching Cubes) -
As illustrated in Fig 6,
only execution of two duality transforms
and the computations of two convex hulls of H points
are required. -
Complexity of these operations
is clearly independent of any resolution parameter Ɛ
Multi convex decomposition - Figure 7
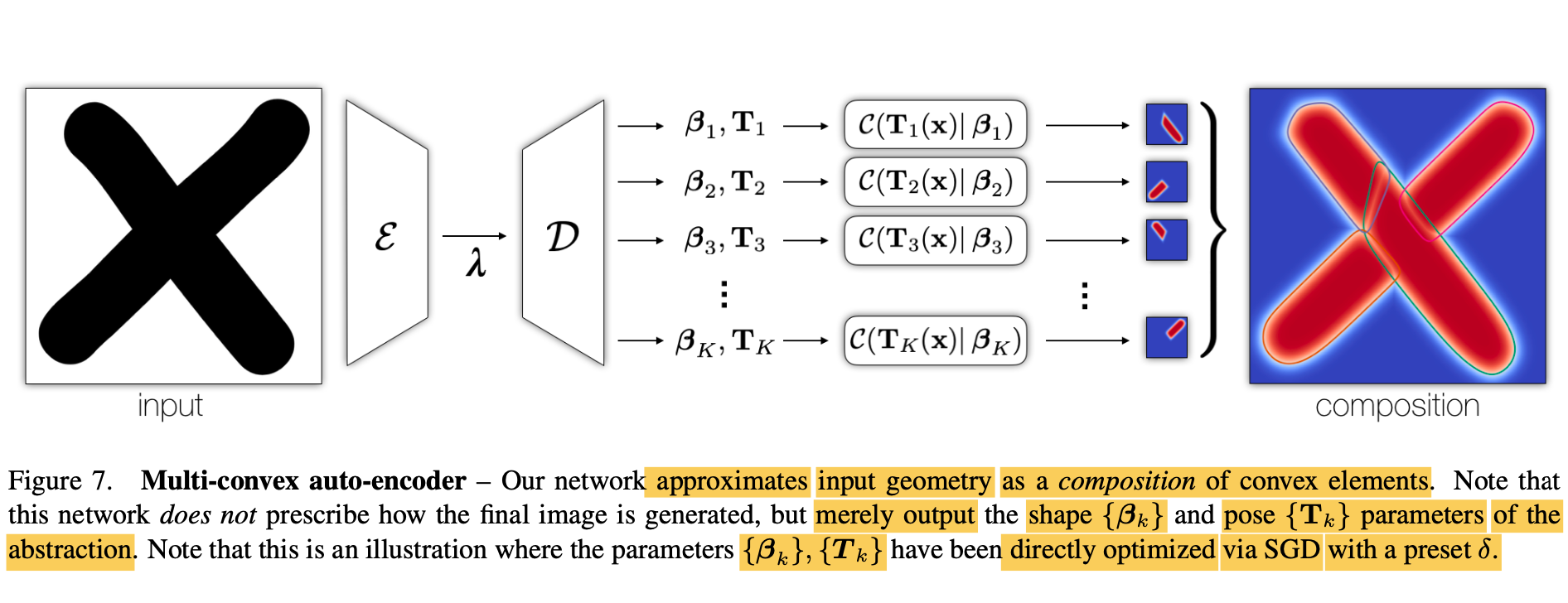
-
Expand the expressivity of model
by representing generic non-conve objects
as compositions of convexes. -
To achieve this task
an encoder Ɛ outputs a low dimensional bottleneck representation
of all K convexes λ that
D decodes into a collection of K parameter tuples. -
Each tuple (indexed by k)
is comprised of a shape code β,
and corresponding transformation T(x) = x + c
that transforms the point from world coordinates
to local coordinated.
(c: predicted translation vector)
Training losses
-
We want the GT indicator function of out object O
to be well approximated:
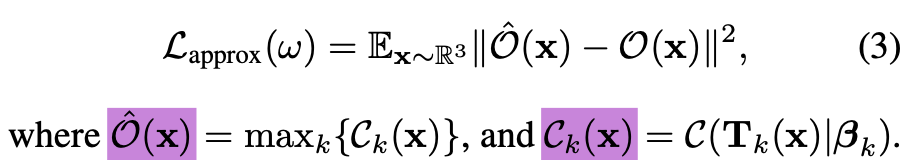
-
Please refer to paper for the deatils of Decomposition loss, Unique parametrization loss, Guidan loss and Localizaion loss.
👨🏻🔬 Experimental Results
- Dataset: ShapeNet
- Evaluation Metric:
1) Volumetric IoU
2) Chamfer-L1 distance = measuring the average between reconstruction accuracy and completeness
3) F-score = percentage of correctly reconstruced surface
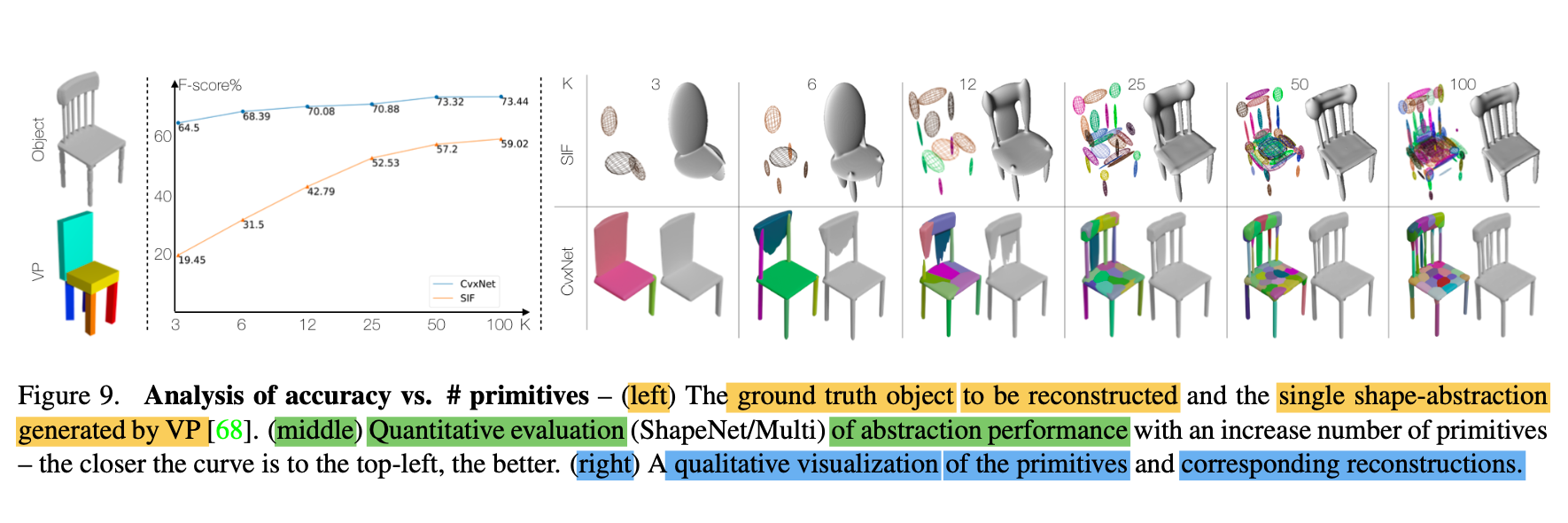
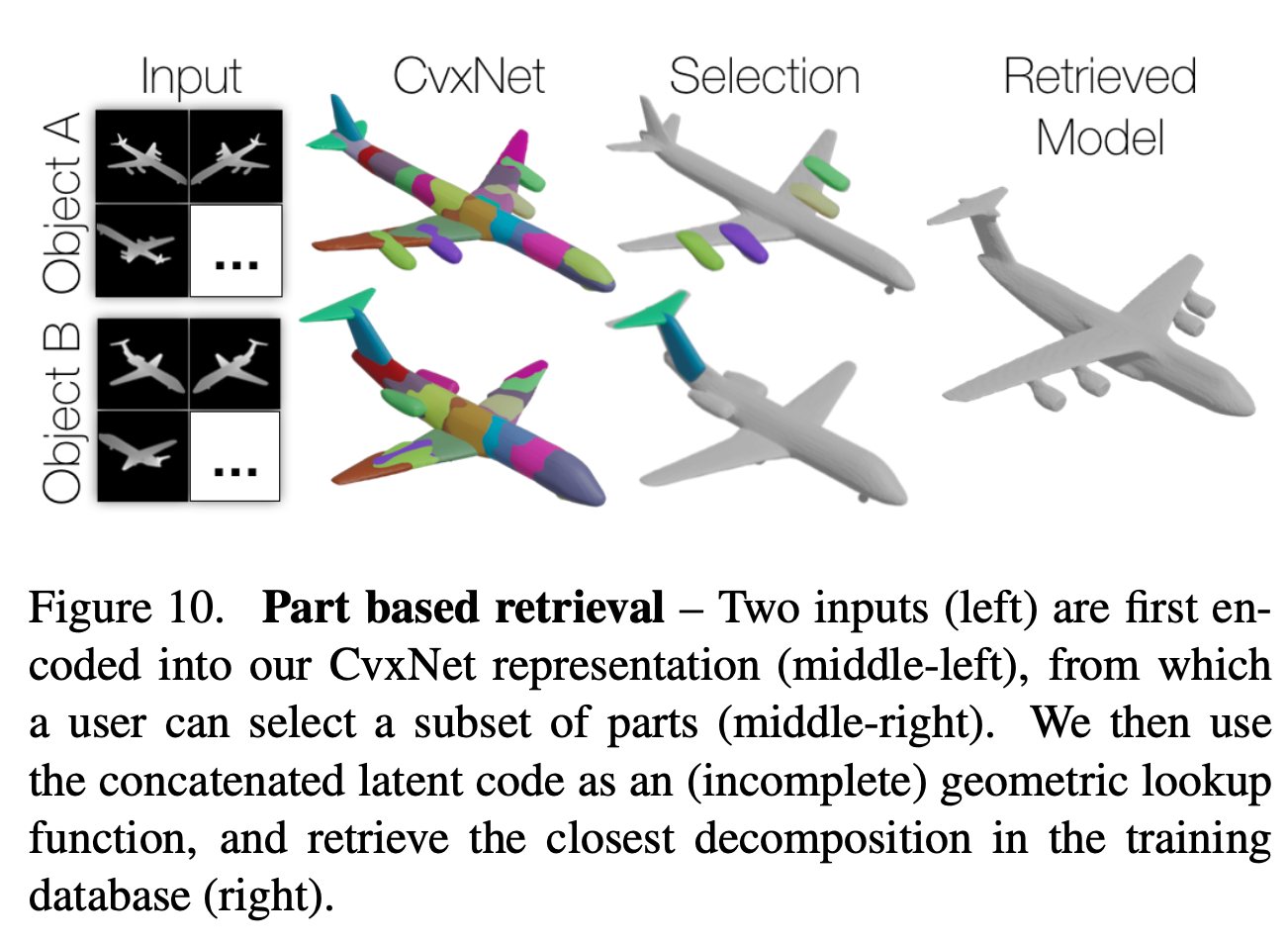
Abstraction - Figure 9, 10, 11
-
As model's convex decomposition is learnt on a shape collection,
the convexes produced by paper's decoder are in natural correspondence
(e.g., paper expects the same k-th convex
to represent the leg of a chair
in the chairs dataset.) -
Paper does so by verifying
whether the k-th component is consistently mapped to
the same PartNet part label; (Fig 11. left) -
Then, we can assign the most commonly associated label
to a given convex
to segment the PartNet point cloud,
achieving a relatively high accuracy; (Fig 11. right)

-
-
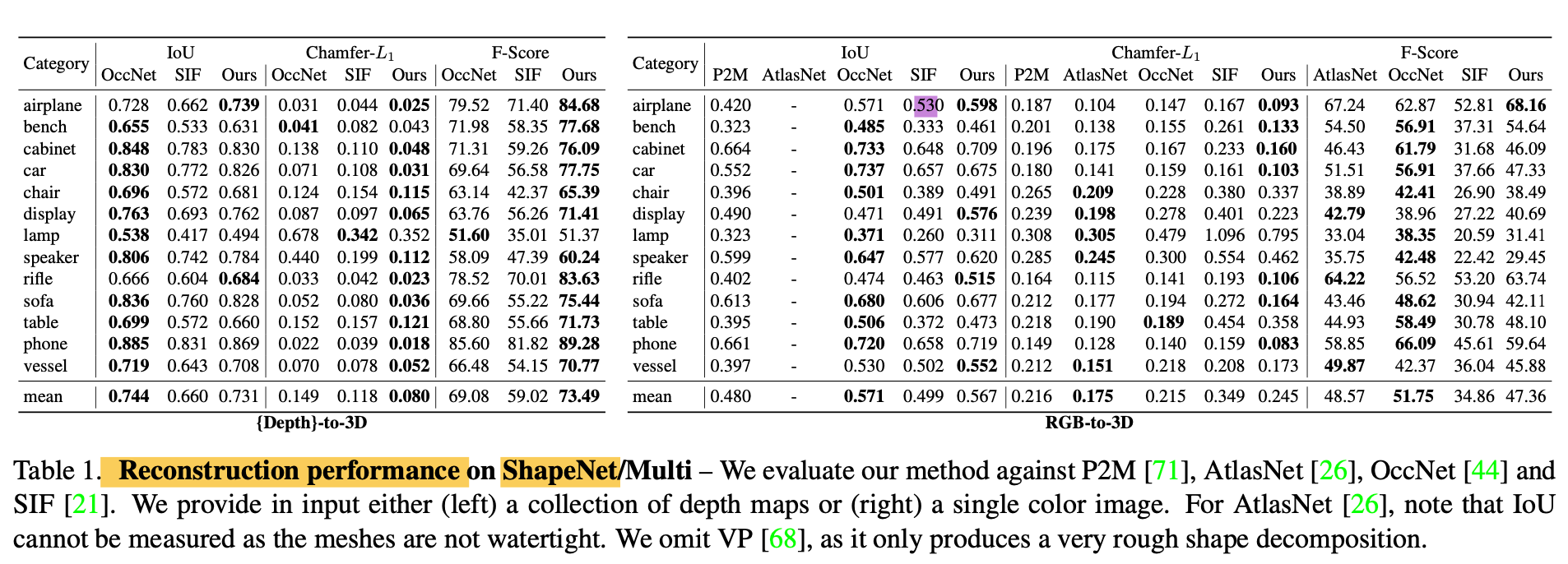
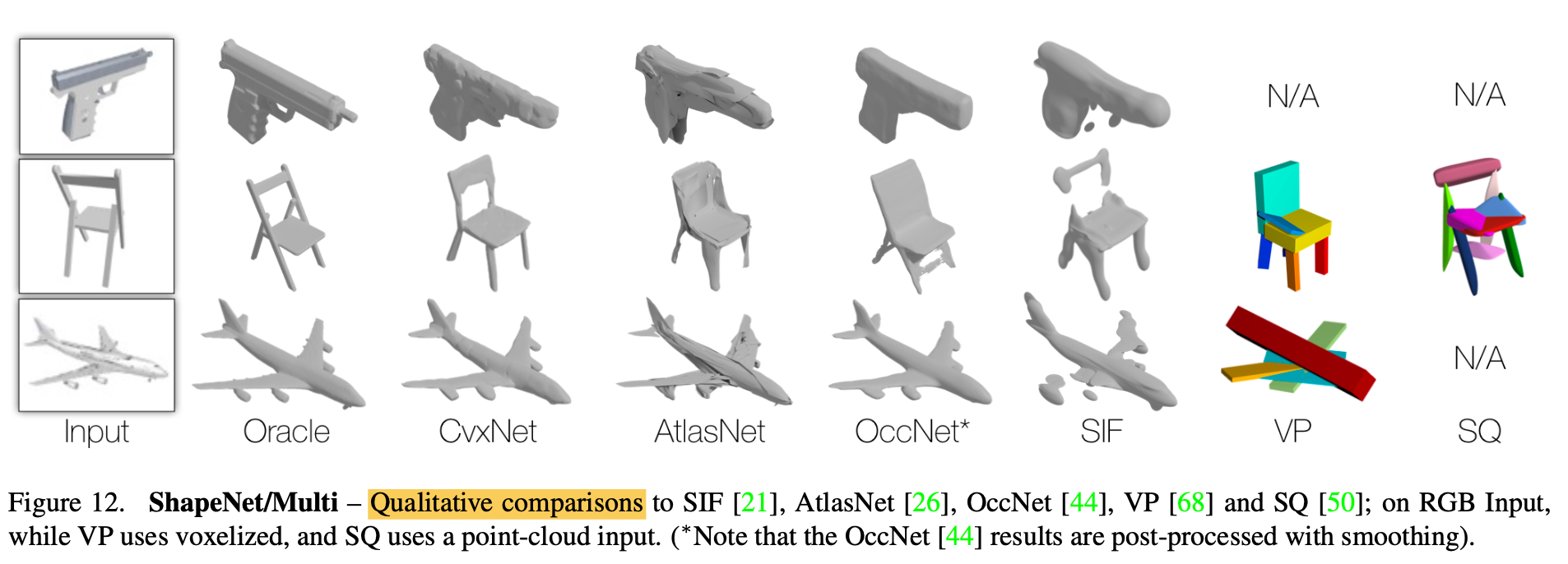
Reconstruction - Table 1 & Figure 12
-
Given inputs: multiple depth map images(Depth-to-3D) &
a single color image (RGB-to-3D) -
-
-
1) CvxNet is consistently better than other
part decomposition methods(SIF, VP and SQ)
which share the common goal of learning shape elements -
2) CvxNet is in general comparable to the SOTA reconstruction methods
-
3) CvxNet is better than the leading technique(OccNet)
when evaluated in terms of F-score, and tested on multi-view depth input.
✅ Conclusion
-
Paper proposes a differentiable representation
of convex primitives
that is amenable to learning. -
Inferred representations are directly usable
in graphics/physics pipelines; -
Paper's self-supervised technique provides
more detailed reconstructions than very recently proposed part-based techniques, -
and even Consistently outperforms the leading reconstruction technique
on multi-view input (OccNet in Table 1)