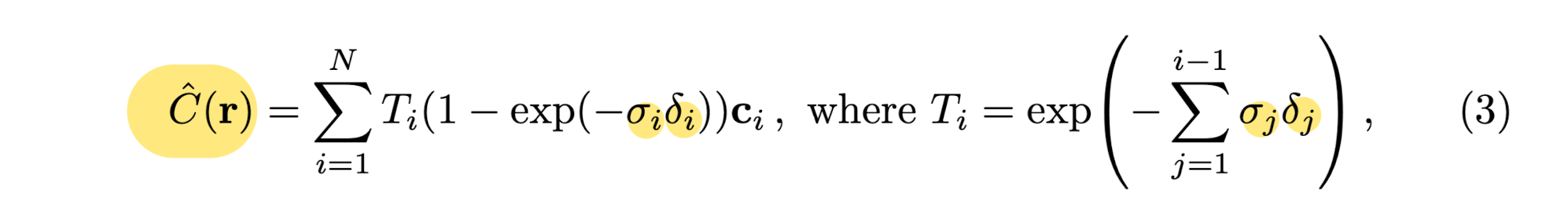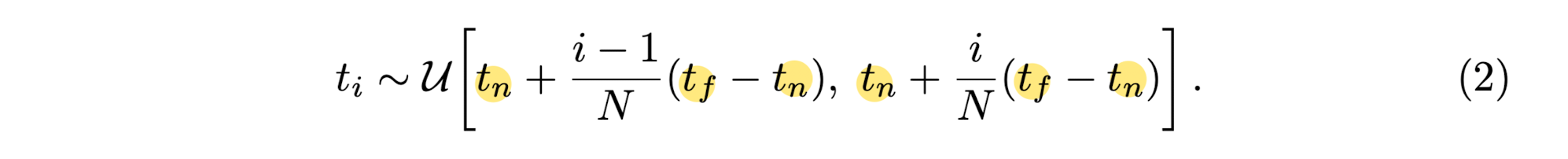🎤 Brief Summary of Paper

• This paper presents a method for
  synthesizing novel views of complex scenes
  by optimizing an underlying continuous volumetric scene function
  using a sparse set of input views.

• Paper's algorithm represents a scene
  using a fully-connected (non-convolutional) deep network,
  whose input: single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ))
  and whose output: volume density
  and view-dependent emitted radiance at that spatial location.

• Paper synthesize views
  by querying 5D coordinates along camera rays
  and use classic volume rendering techinques
  to project the output colors and densities into an image.

• Because volume rendering is naturally differentiable,
  the only input required to optimize paper's representation
  is a set of images with known camera poses.

🔑 Key Technical Contributions

• The first continuous neural scene representation
  that is able to render high-resolution photorealistic novel views of real objects
  and scenes from RGB images captured in natural settings.

• An approach for representing continuous scenes
  with complex grometry and materials as 5D neural radiance fields, parameterized as basic MLP networks.

• A differentiable rendering procedure
  based on classical volunme rendering techniques,
  which paper uses to optimize these representations
  from standard RGB images.
  This includes hierarchical sampling strategey
  to allocate the MLP's capacity
  towards space with visible scene content.

• A positional encoding to map each input 5D coordinate into a higher dimensional space,
  which enables us to successfully optimize NeRF
  to represent high-frequency scene content.

⭐ Methods

Overview

• Paper describes how to effectively optimize neural radiance fields
  to render photorealistic novel views of scenes
  with complicated geometry and appearance.
  

• To render neural radiance field (NeRF) form a particular view point,

1) march camera rays through the scene
➡️ to generate a sampled set of 3D points

2) use those points and their corresponding 2D viewing direction
as input to the NN,
to produce an output set of colors and densities

3) use classical volume rendering techniqures to accumulate those colors and densities into a 2D image.

Because this process is naturally differentiable,
we can use gradietn descent to potimize this model
by minimizing the error between each observed image
and the corresponding views renderd from our representation.

Minimizing this error across multiple views encovurages the network
to predict a coherent model of the scene
by assigning high volume densities and accurate colors
to the locations that contain the true underlying scene content.

• Below Figure 2 visulalizes this oveall pipeline.

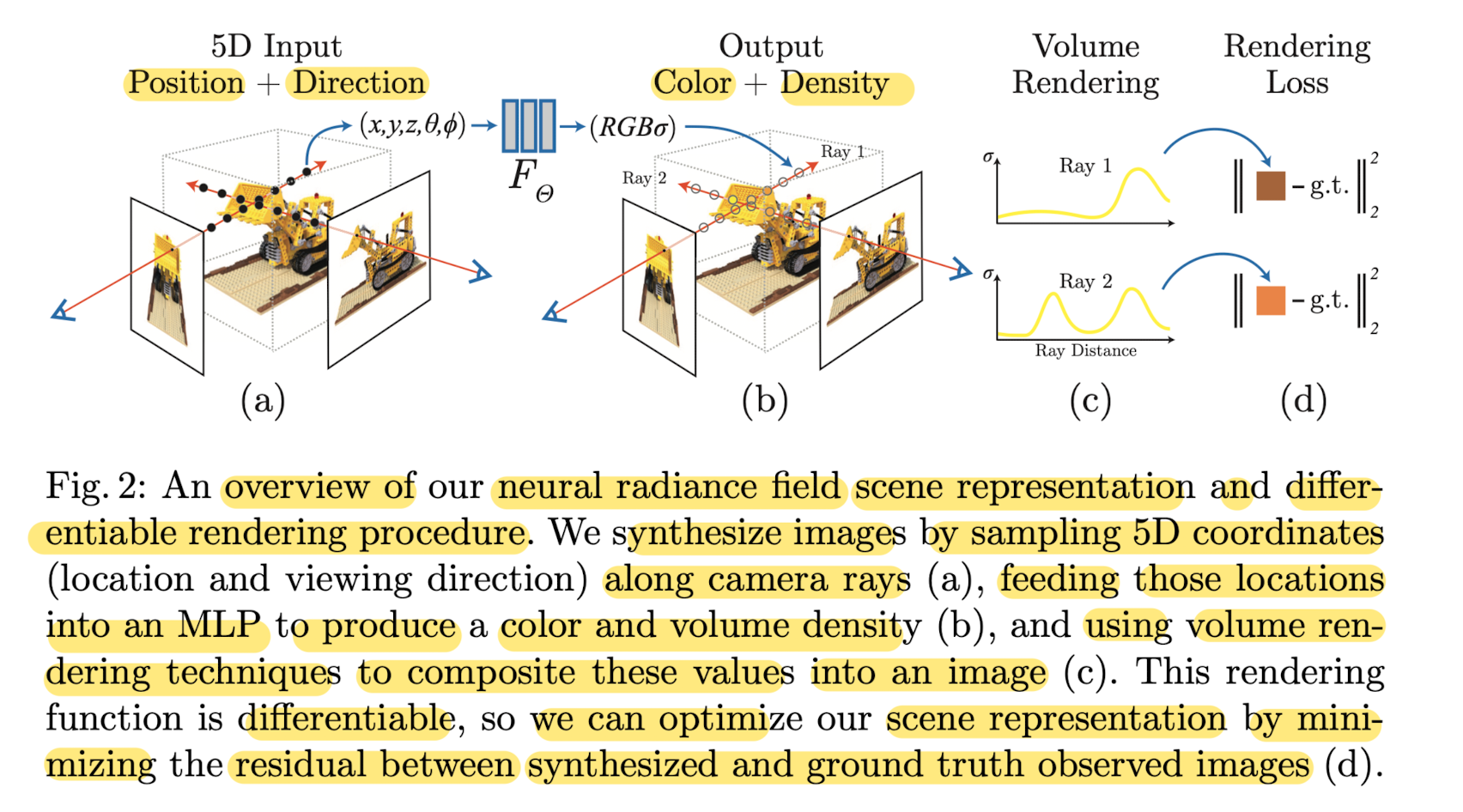
Neural Radiance Field Scene Representation

• Paper represents a continuous scene as a 5D vector-valued function
  whose input: 3D location x = (x, y, z) and 2D viewing direction (θ, φ),
  whose output: emitted color c = (r, g, b) and volme density σ
  (In practice, direction is expressed by a 3D Cartesian unit vector d)

• Paper approximate this continuous 5D scene representation
  with an MLP network FΘ: (x, d) -> (c, Θ)
  and optimize its weights Θ to map from each input 5D coordinate
  to its corresponding volume density and directional emitted color.

-- ✂️ --

• Paper encorages the representation to be multiview consistent by restricting the network
  to predcit the volume density σ ➡️ as a function of only the location x,
  while allowing the RGB color c ➡️ to be predicted as a function of both location x, and viewing direction (θ, φ)

To accomplish this,

• the MLP FΘ first processes
  the input 3D coordinate x with 8 fully-connected layers
  (using ReLU actiations and 256 channels per layer),
  and outputs volume density σ and 256-dimensional feature vector.

• This feature vector is then concatenated with the camera ray's viewing direction (c, Θ)
  and passed to one additional fully-connected layer
  (using a ReLU activation and 128 channels)
  that output the view-dependent RGB color c.

-- ✂️ --

• See Fig.3 for an example of
  how method uses the input vuewing direction (c, Θ)
  to represent non-Lambertian effeects.
  

• As shown in Fig.4, a model trained without view dependence (only x an input)
  has difficulty representing specularities.
  

---

Volume Rendering with Radiance Fields

• Paper's 5D neural radiance field represents a scene
  as the volume density and irectional emitted radiance at any point in space.

• Render the color of any ray passing through the scene
  using principles from classical volume rendering.

---

• Volume density σ(x) can be interpreted as
  the differential probability of a ray terminating at an infinitesimal particle
  at location x

• The expected color C(r) of camera ray r(t) = o + td
  with near and far bounds tn and tf is:
  

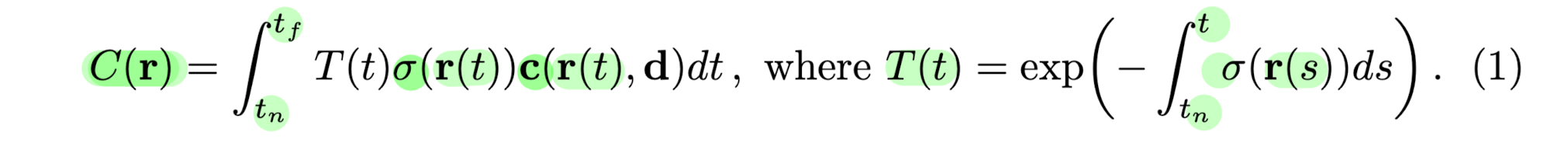
• T(t) denotes the accumulated transmittance along the ray from tn to t,
  i.e., the probability that the ray travels from tn to t without hitting any other particle.

• Rendering a view from paper's continuous neural radiance field requires
  estimating this integral C(r)
  for a camera ray, traced through each pixel of the desired virtual camera.

---

• Paper numerically estimates this continuous integral using quadrature.

• Paper used a stratified sampling approach
  where they partition [tn, tf] into N evenly-spaced bins
  and then draw one sample uniformly at random from within each bin:
  

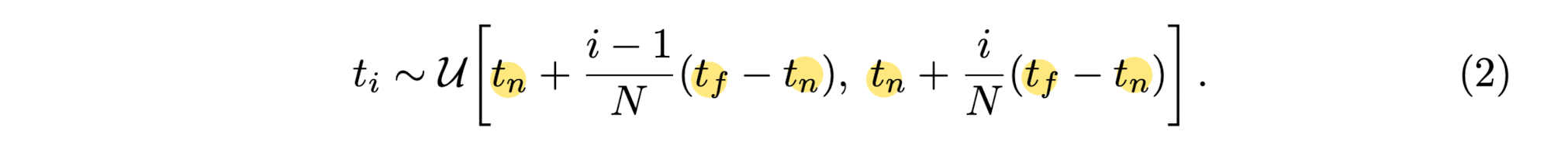
• Although paper used a discrete set of samples to estimate the integral,
  stratified sampling enables to represent a continuous scene representation
  because it results in the MLP being evaluated at continuous positions
  over the course of optimization.

• Paper used these samples to estimate C(r) with the quadrature rule,
  discussed in the volume rendering review paper.
  

---

Optimizing a Neural Radiance Field

• In the previous sections, paper described the core components
  necessary for modeling a scene as a neural radiance field
  and rendering novel views from this representation.

• However, paper observed that these components are not sufficient for acheiving SOTA quality.

• Thus, paper introduces two improvements
  to enable representing high-resolution complex scene
  first: positional encoding of the input coordinates
  that assits the MLP in representing high-frequency functions
  second: hierarchical sampling procedure
  that allows to efficiently sample this high-frequency representation.

1) Positional Encoding

• Paper found that having the network FΘ directly operate on xyzθφ input coordinates
  results in rendering that perform poorly at representing high-frequency variation in color and geometry.

• Paper leverages findings of other recent work ,
  which shows that deep networks are biased
  towards learning lower frequency functions,
  and mapping the inputs to a higher dimenstional space using high frequency functions
  before passing them to the network
  enables better fitting of data that contains high frequency variation.

• Paper leverages these findings in the context of neural scene representations,
  and show that reformulating FΘ as a composition of two functions FΘ = F'Θ ◦ γ,
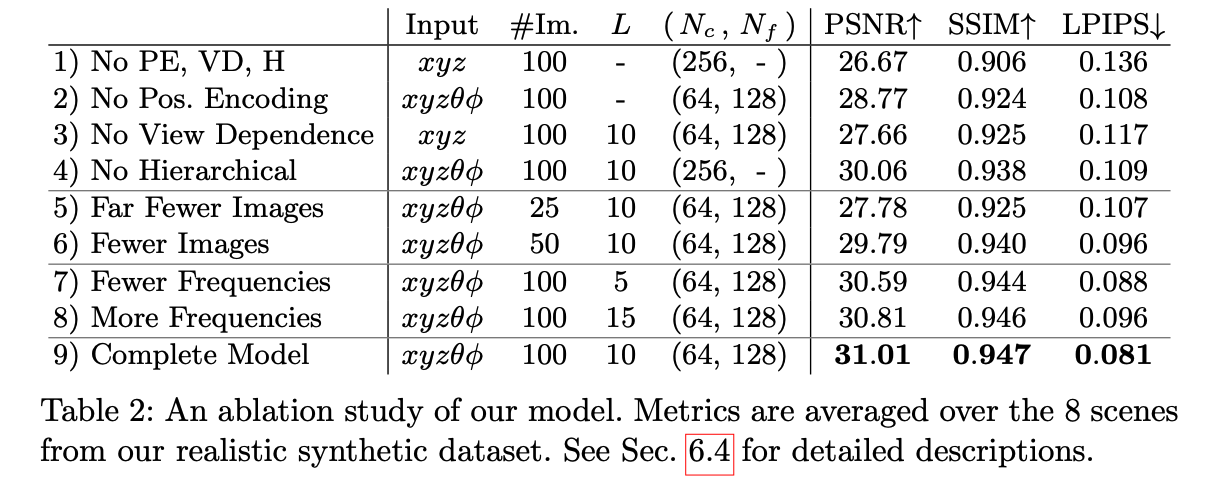
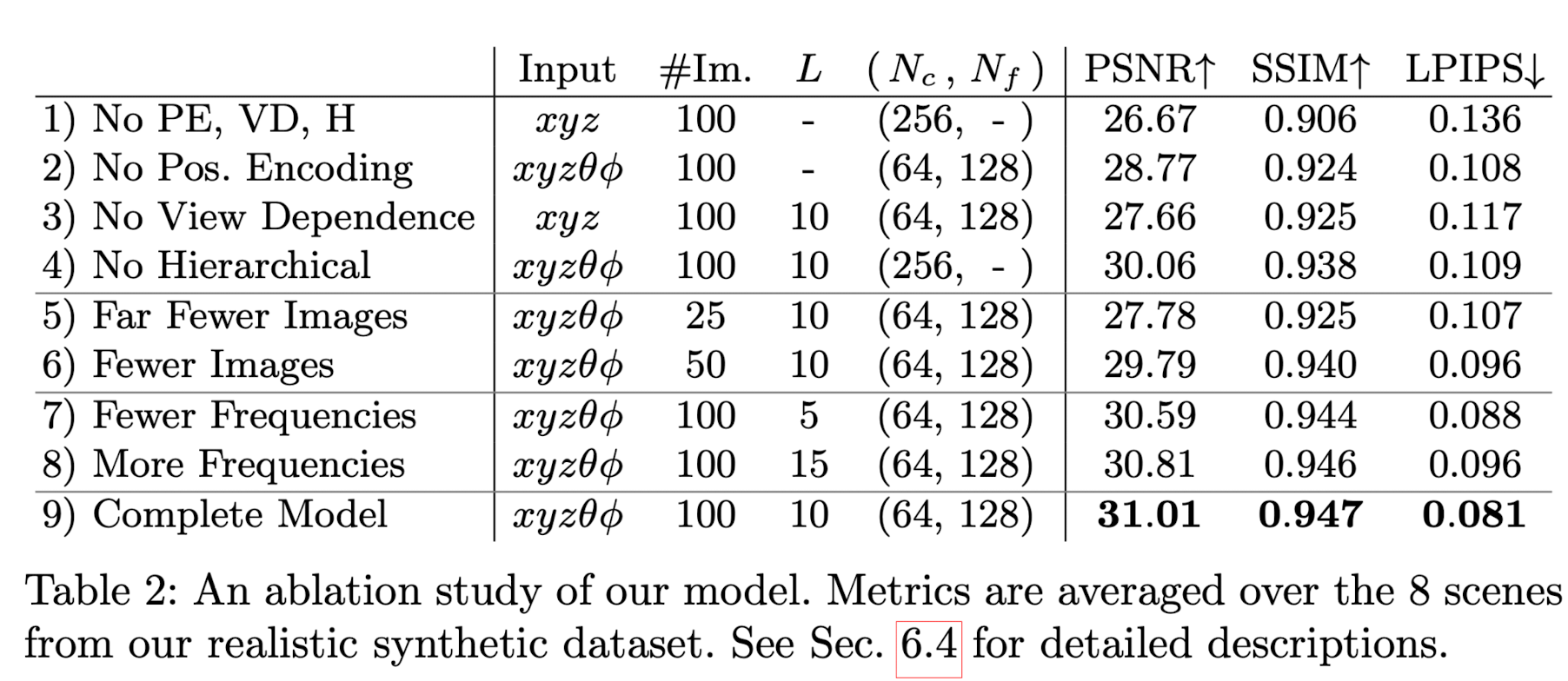
  one learned and one not, significantly imrpoves performance, (as below Fig4 and Table 2)
  where γ: mapping from ℝ into a higher dimensional space ℝ^(2L),
  and F'Θ: is still simply a regular MLP.
  Encoding functions paper uses is:
  
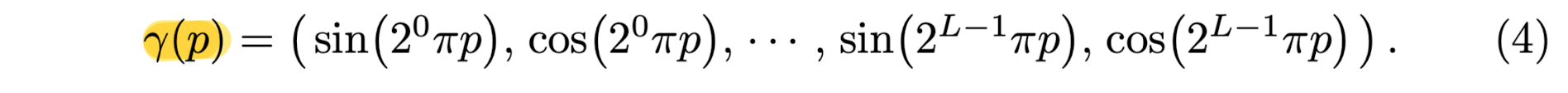
  This function γ(⋅) is applied separately to each of the three coordinate values in x
  (which are normalized to lie in [-1, 1])
  and to the three components of the Cartesian viewing direction unit vector d
  (which by construction lie in [-1, 1]).
  (In paper's experiments, set L = 10 for γ(x) and L = 4 for γ(d)

• 
• 

2) Hierarchical volume sampling

• paper's rendering strategey of densely evaluating the neural radinace field network at N query points along each camera ray is inefficient:
  free space and occluded regions
  that do not contribute to the rendered image are still sampled repeatedly

• Paper drew inspiration from early work in volume rendering,
  and proposed hierarchical representation that increases rendering efficiency
  by allocating samples proportionally to their expected effect
  on the final rendering.

• Instead of just using a single network to represnt the scene,
  paper simulataneously optimize two networks:
  one coarse and one fine.

1) First sample a set of Nc locations using stratified sampling,

2) and evaluate the coarse network at these locations
as described in Eqns.2 and 3

• 
• 

3) Given the output of this coarse network,
then produce a more informed sampling of points along each ray,
where samples are biased towards the relevant parts of the volume.

To do this,
➡️ first rewrite the alpha composited color form the coarse network

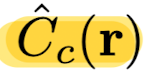
in Eqn.3
as a weighted sum of all sampled colors *ci along the ray:

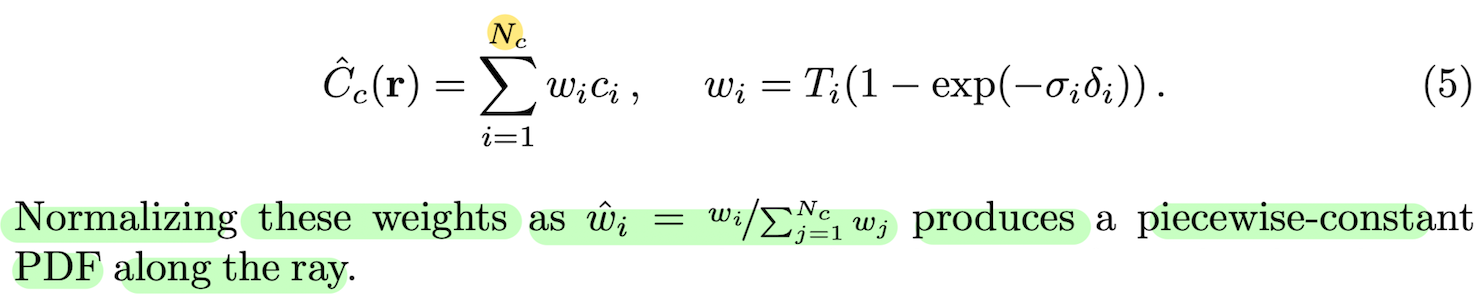
4) sample a second set of Nf locations from this distribution
using inverse transform sampling,

5) evaluate fine network at the union of the first and second set of samples

6) compute the final rendered color of the ray

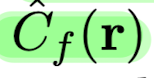
using Eqn.3
but using all Nc + Nf samples.

• This procedure allocates more samples to regions
  which we expect to contain visible content

3) Implementation details

• Paper optimizes a seaparate neural continuous volume representation network for each scene.

• This requires only
  a dataset of captured RGB images of the scene,
  the corresponding camera poses
  and intrinsic parameters,
  and scene bounds.

• At each optimization iteration,
  paper randomly samples a batch of camera rays from the set of all pixels in the dataset,
  and then follow the hierarchical samping
  to query Nc sample form the coarse netowrk
  and Nc + Nf samples from the fine network.

• Then use the volume rendering procedure,
  to render the color of each ray from both sets of samples.

• Paper's loss is simply the total squared error betwwen
  the rendered and true pixel colors for both the coarseand fine renderings:
  where R : set of rays in each batch,
  C(r), C hat c(r), C hat f(r): GT, coarse volume predicted, and fine volume predicted RGB colors
  for ray r respectively.
  

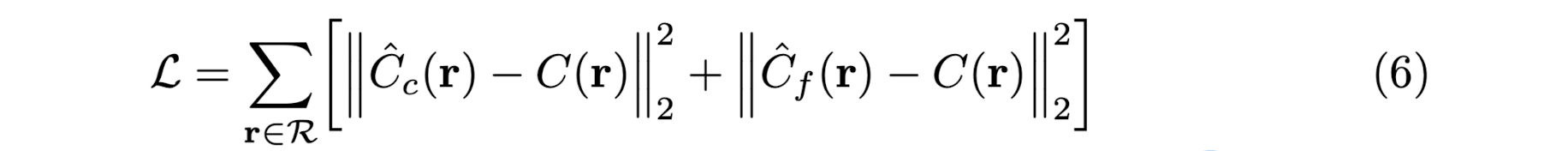
• Note that even though the final rendering comes from
  C hat f(r),
  paper also minimizes the loss of C hat c (r)
  so that the weight distribution from the coarse network can be used to allocate samples in the fine network.

• Paper's experiments
  -batch size: 4096 rays,
  each sampled at Nc = 62 coordinates in the coarse volume
  and Nf = 128 additinoal coordinates in the fine volume
  -Adam optimizer with a leraning rate that begins at 5x10^(-4)
  and decays exponentially to 5 x 10^(-5) over the course of optimization.

👨🏻‍🔬 Experimental Results

Qunatitative Results

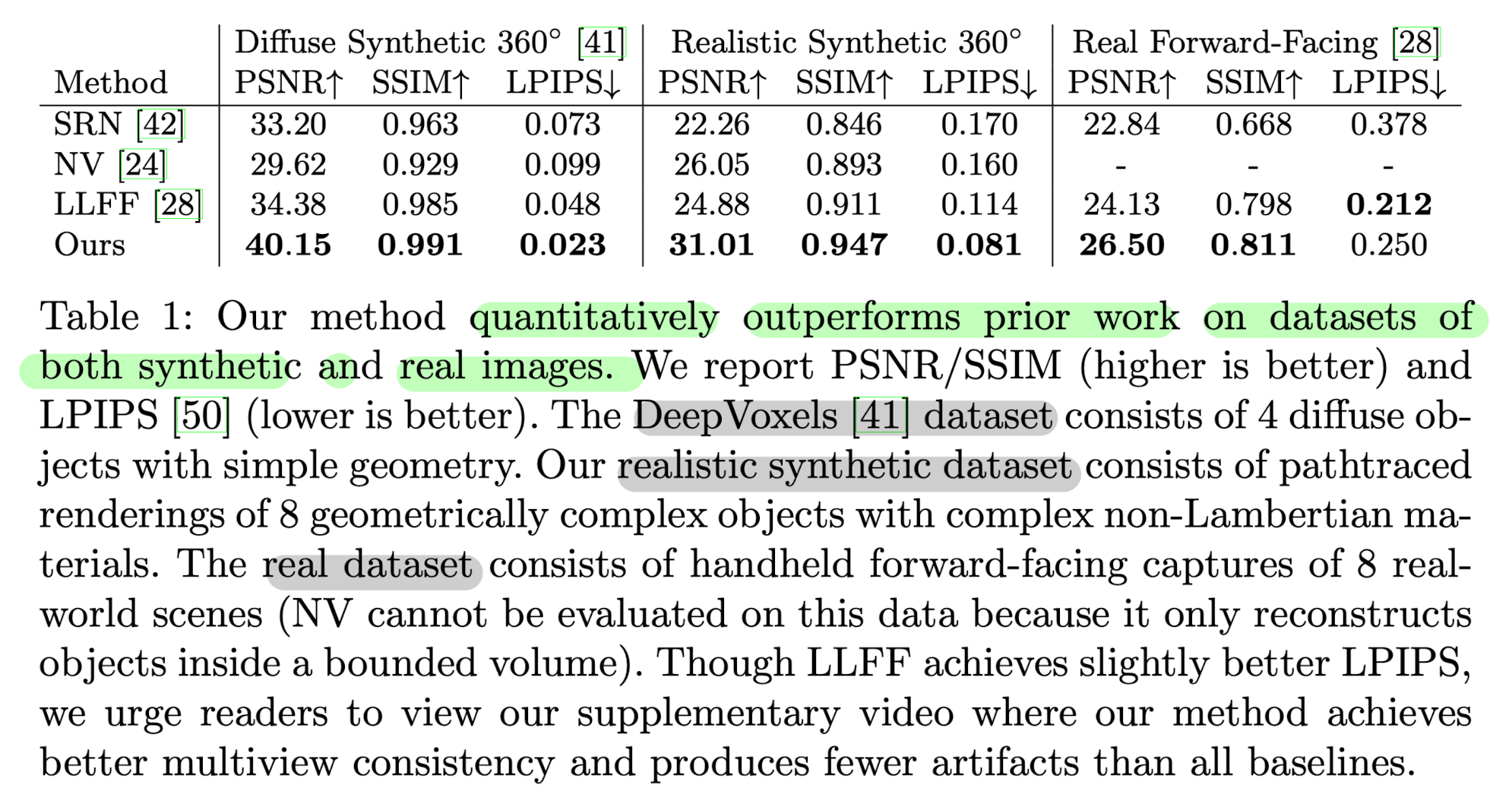
Comparison

Ablation study

✅ Conclusion

• Paper's work directly addresses deficiencies of prior work
  that uses MLPs to represent objects and scenes as continuous functions.

• Paper demonstreated that representing scene as 5D neural radiance fields
  (an MLP that ouputs volume density and view-dependent emitted radiance as a function of 3D location and 2D viewing direction)
  produces better renderings that the previously-dominant approach of training deep convolutional networks
  to output discretized voxel representations.

🤔 Limitations

• Although paper proposed hierarchical sampling strategey
  to make rendering more sample-efficient (for both training and testing),
  there is still much more progress to be made in investigating techniqures
  to efficiently optimize and render neural radiance fields

• Another direction for future work is interpretability:
  sampled representations such as voxel grids and meshes
  admit reasoning about the expected quality of rendered views and filure modes,
  but is is unclear how to analyze these issues
  when we encode scenes in the weights of a deep NN.