🚀 Motivations

• Classical and compact surface representations such as triangle or quad meshes pose problems in training beacause possible needs to deal with an unknown number of vertices and arbitrary topology.

• These challenges have limited the quality, flexibitiy and fidelity of deep learning approaches when attempting to either input 3D data for processing or produce 3D inferences for object segmentation and reconstruction.

🔑 Key Contribution

• This paper presents generative 3D modeling which is efficient, expressing, and fully continuous with approach using concept of a SDF, but learning a generative model to produce such a continuous field.

• This paper suggests The formulation of generative shape-conditioned 3D modeling with a continuous implicit surface.

• The first to introduce the auto-decoder as a learning method for 3D shapes based on a probabilistic.

• The demonstration and application of this formulation to shape modeling and completion.

⭐ Modeling SDFs with Neural Networks

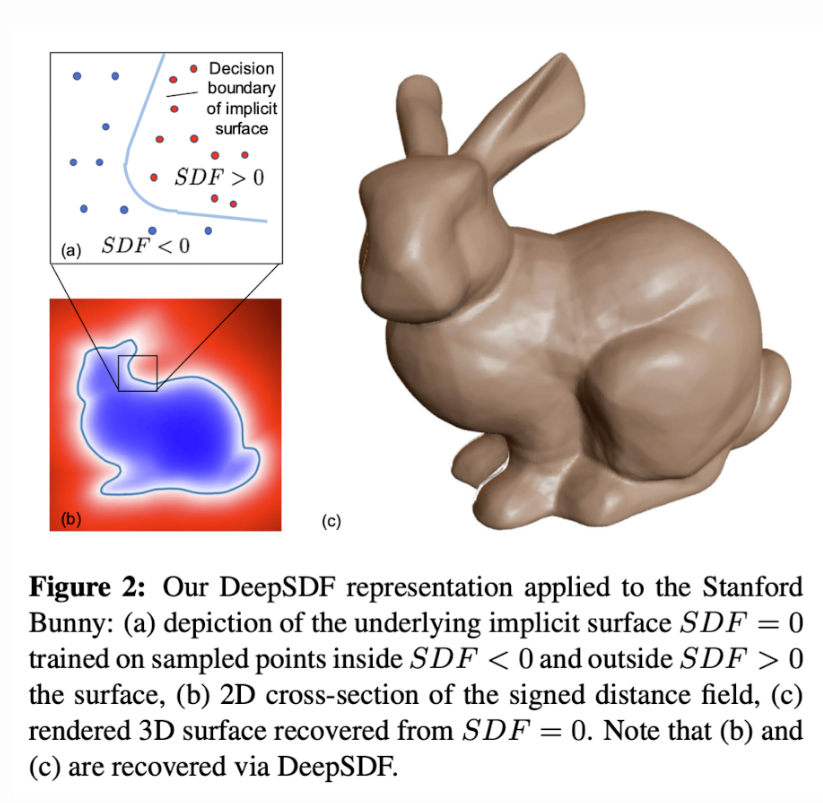
• Proposed continuous representation can be understood as a learned shape-conditioned classifier for which the decision boundary is the surface of the shape itself. (as Fig 2)

• DeepSDF describe modeling shapes as the zero iso-surface decision boundaries of feed-forward networks trained to represent SDFs.

• A signed distance function is a continuous function that, for a given spatial point, outputs the point's distance to the closest surface, whose sign encodes whether the point is inside(negative) or outside(positive) of the watertight surface.

• The underlying surface is represented by the iso-surface of SDF(·) = 0.

• A view of this implicit surface can be rendered through Marching Cubes.
  

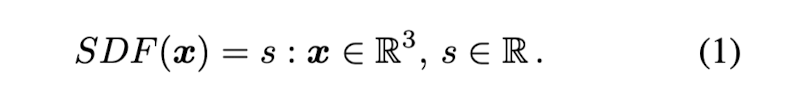
• Key idea is to directly regress the continuous SDF from point samples using deep NN.

• The resulting trained network is able to predict the SDF value of a given query position, from which we can extract the zero level-set surface by evaluating spatial samples.

• Such surface representation can be intuitively understood as a learned binary classifier for which the decision boundary is the surface of the shape itself.

---

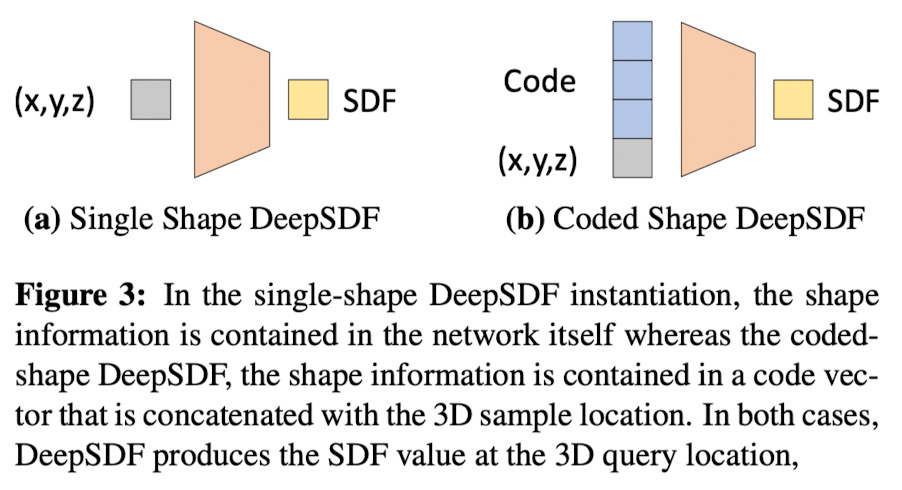
• To train a single deep network for a given target shape as Fig 3a,
  

• Given a target shape, prepare a set of pairs X composed of 3D point samples and their SDF values.
  

---

---

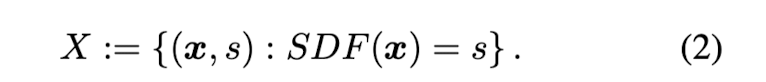
• 𝛿 is introduced to control the distance from the surface over expectation to maintain a metric SDF. (Larger value of 𝛿: fast ray-tracing, Smaller value of 𝛿: details neart the surface)

🌟 Learning the Latent Space of Shapes

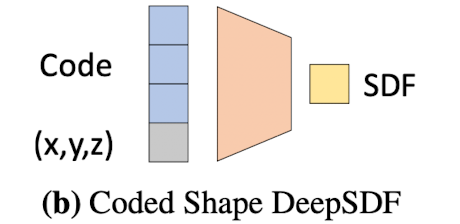
• A latent vector z is introduced, which can be thought of as encoding the desired shape, as a second input to the NN as depicted in Fig 3b

• Mapping this latent vector to a 3D shape represented by a continuous SDF.
  

• For some shape indexed by i, fθ is a function of latent code zi and a query 3D location x, and outputs the shape's approximate SDF.
  

---

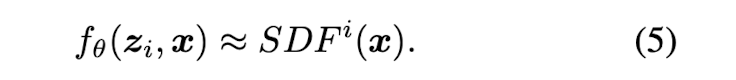
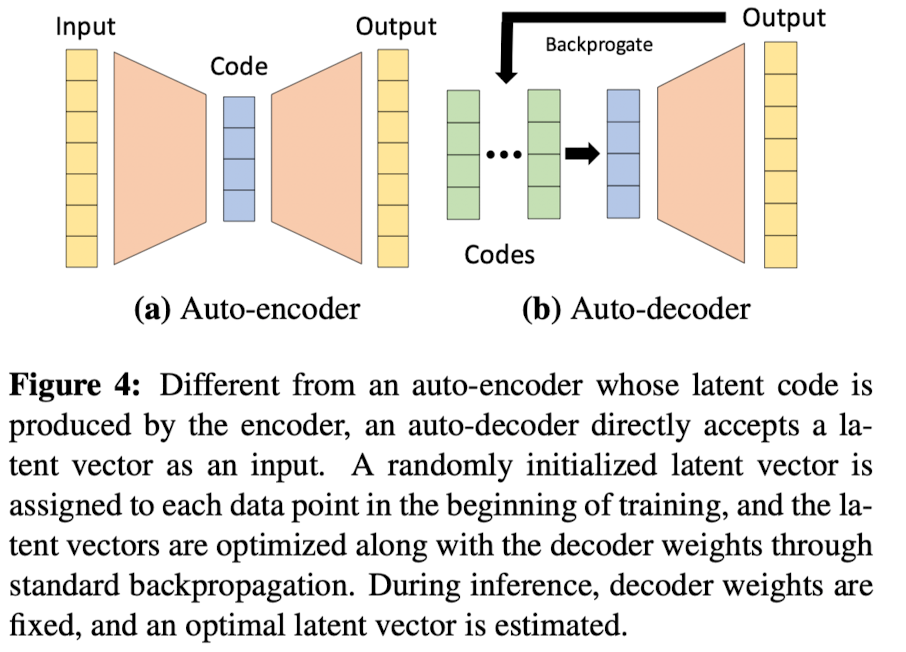
• Using an auto-decoder for learning a shape embedding without an encoder as depicted in Fig 4. ➡️ applying auto-decoder to learn continous SDFs leads to high quality 3D generative models.
  

• Further, this paper developed a probabilistic formulation for training and testing the auto-decoder that introduces latent space regularization for improved generalization.

Auto-decoder-based DeepSDF Formulation

• 

• The posterior over shape code zi given the shape SDF samples Xi can be composed as: (where θ parameterizes the SDF likelihood)
  

• 

• 

• 

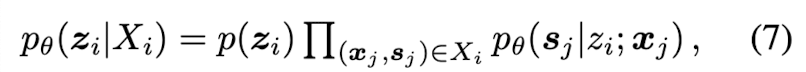
• To incorporate the latent shape code, this paper stacked the code vector and the sample locations as Fig 3b.
  

👨🏻‍🔬 Experimental Results

Representing Known 3D shapes

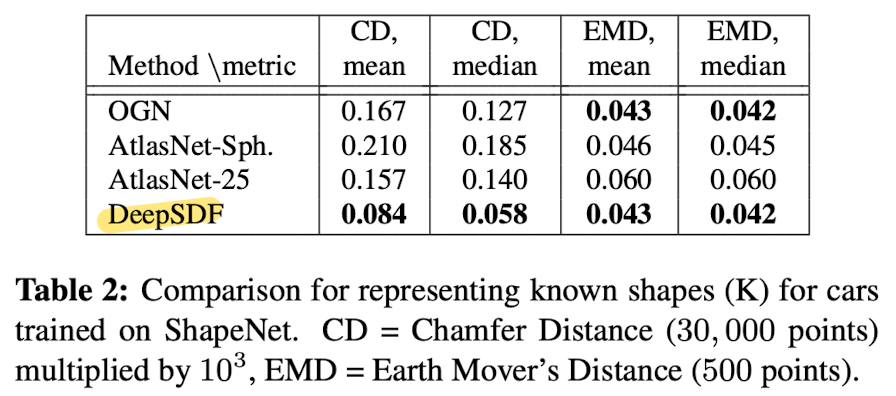
• Evaluation the capacity of the model to represent known shapes, i.e. shapes that were in the traing set, from only a restricted-size latent code.
  -Table2 shows DeepSDF beats OGN and AtlasNet in CD against the true shape computed with a larger number of points (30,000).
  -The difference in EMD is smaller because 500 points do not well capture the additional precision.
  

Representing Test 3D shapes(auto-encoding)

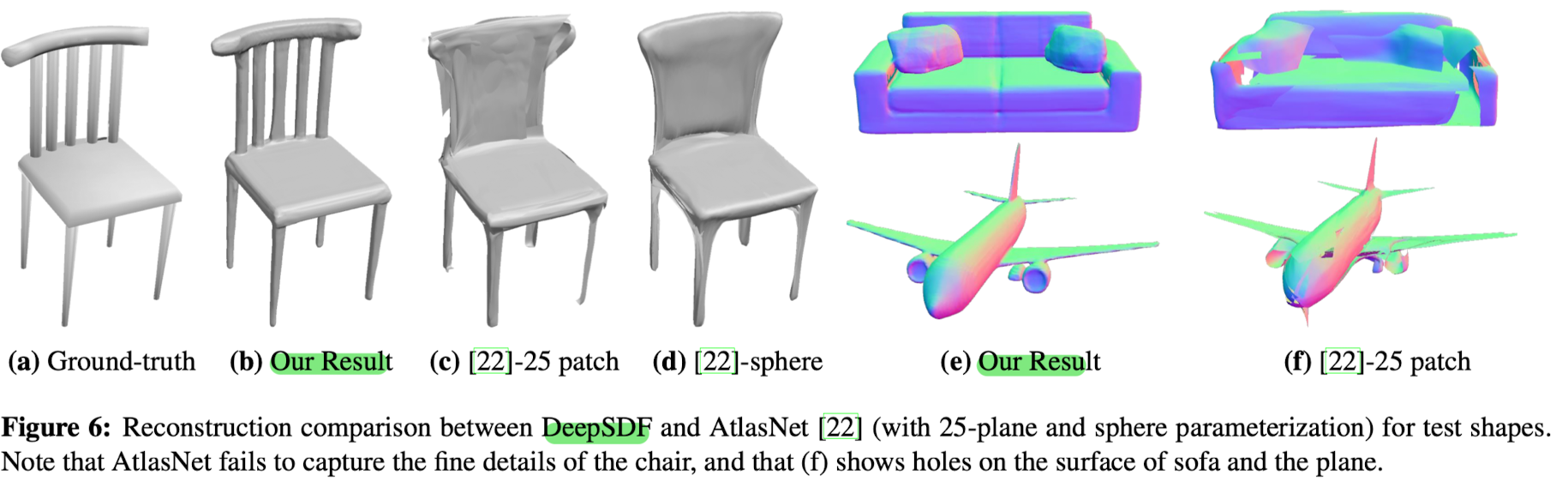
• DeepSDF outperforms AtlasNet.
• AtlasNet performs well on shapes without holes, but struggles on shapes with holes.
  
  

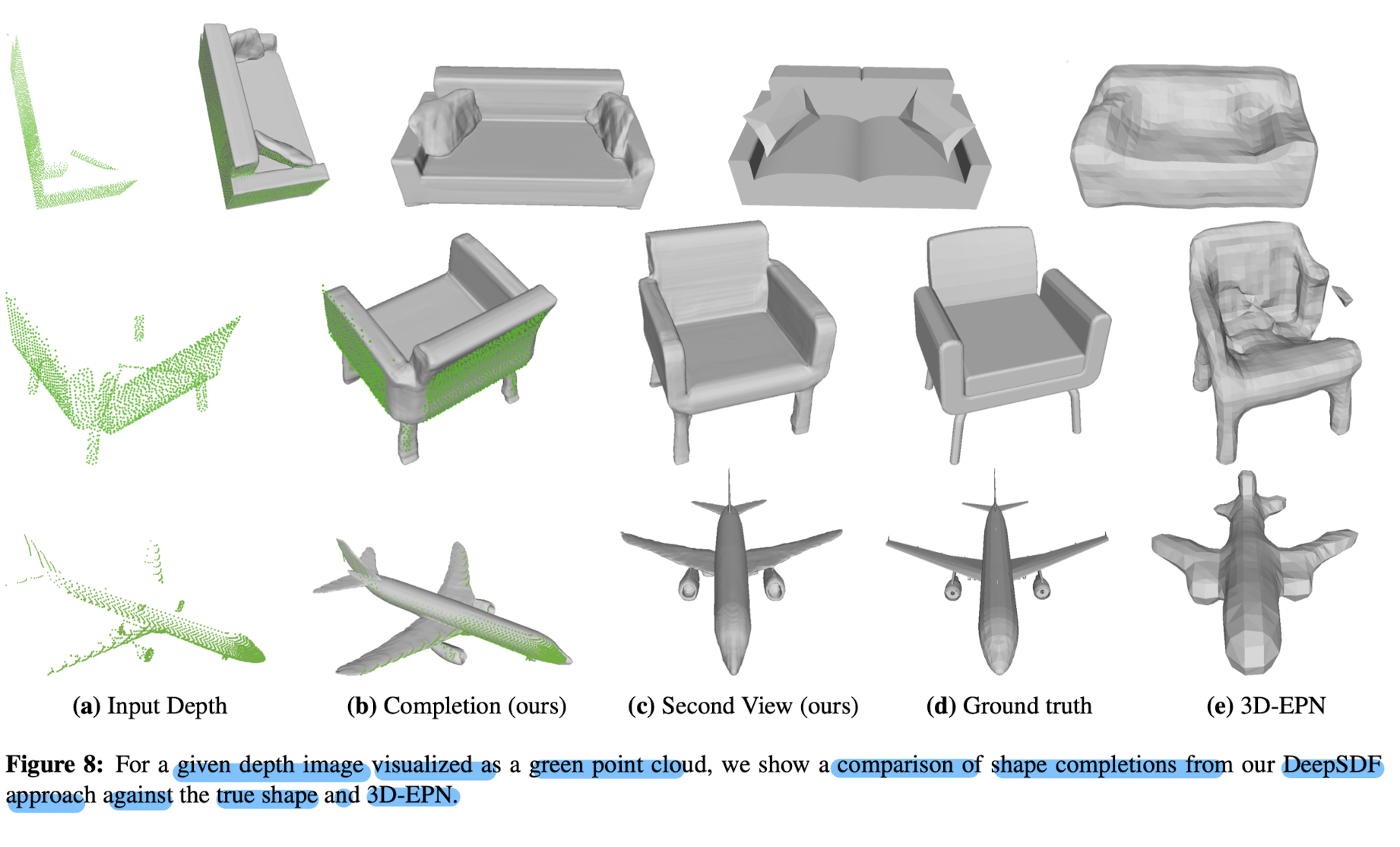
Shape Completion

• Paper's continuous SDF approach produces more visually pleasing and accurate shape reconstructions.
• 
• 

Latent Space Shape Interpolation

• The results suggests that the embedded continuous SDF's are of meaningful shapes.
• Representation extracts common interpretable shape features, such as the arms of a chair, that interpolate linearly in the latent space.

✏️ Limitations

• Shape Completion (auto-decoding) takes considerable time during inference due to the need for explicit optimization over the latent vector.

• DeepSDF currently assumes models are in a canonical pose and such completion in-the-wild requires explicit optimization over a SE(3) transformation space increasing inference time.