🚀 Motivations

• Recents attempts to encode 3D geometry for use in deep learning include view-based projections, volumetric grids and graphs.
  ➡️ This paper focuses on the representation of 3D point clouds.

• All the aforementioned encoding, while effective in their targe tasks(e.g. rendering or acquisition), are hard to manipulate directly in their raw form.

• These representations are not well suited for the design of generative models via classical statistical methods.

• There is no universally accepted method for the evaluation of generative models.

🔑 Key Contribution

• Use of deep architectures for learning representations and introduce the first deep generative models for point clouds.

• A new AE architecture for point clouds

• The first set of deep generative models for point clouds, able to synthesize point clouds with measurably high fidelity to, and good coverage of both the training and the held-out data.
  ➡️ This paper proposes to first train an AE to learn a latent representation and then train a generative model(l-GANs) in that fixed latent space.
  ➡️ l-GANs are easier to train and achieve superior reconstruction and better coverage of the data distribution.

• Fidelity and coverage metrics for generative models, based on an optimal matching between two different collections of point clouds.
  ➡️ Paper's coverage metric can identify parts of the data distribution that are completely missed by the generative model.

⛰️ Background

1. Metrics
1) EMD
solution of a transportation problem which attepts to transform one set to the other. For two equally sized subsets, and where φ is a bijection, their EMD is defined by

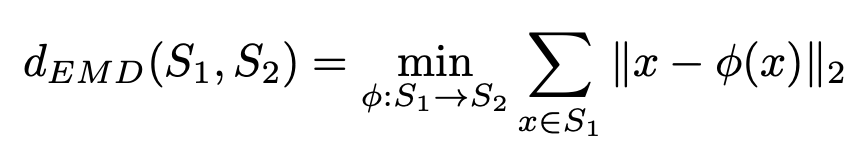
2) CD
CD measures the squared distance between each point in one set to its neares neighbor in the other set.

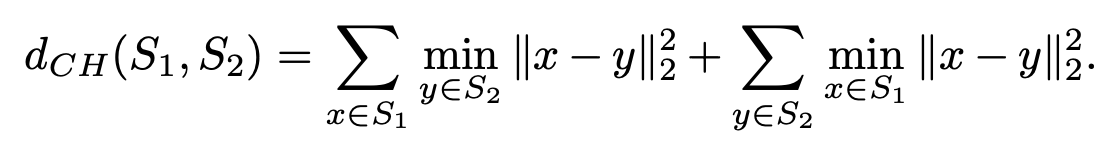
2. Fundamental building blocks
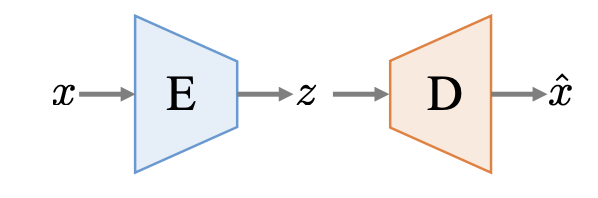
1) Autoencoders(AE)

• It learns to reproduce its input.
• Encoder(E) learns to compress a data point x into its latent representation z.
• Decoder(D) can then produce a reconstruction x hat of x, from its encoded version z.
  

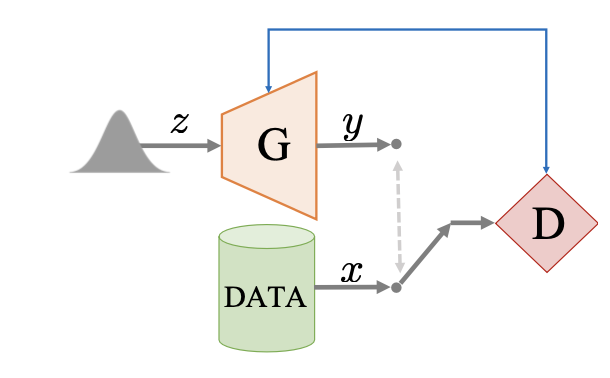
2) Generative Adversarial Networks

• The basic architecture is based on a adversarial game between a generator(G) and a discriminator(D).
• Generator aims to synthesize samples that look indistinguishable from real data by passing a randomly drawn sapme from a simple distribution z ~ pz through generator function.
• Discriminator is tasked with distinguishing synthesized from real samples.
  

3) Gaussian Mixture Model

• Probabilistic model for representing a population whose distribution is assumed to be multimodal Gaussian.

⭐ Methods

📈 Evaluation Metrics for Generative Models

1) JSD(Jense-Shannon Divergence between marginal distribution)

• Measure the degree to which point clouds of A tend to occupy similar locations as those of B.
• It eavaluates the similarity beteween A and B in coarser way, via marginal statistics.
• It requires pre-aligned ata, but is is computationally friendlier.
  

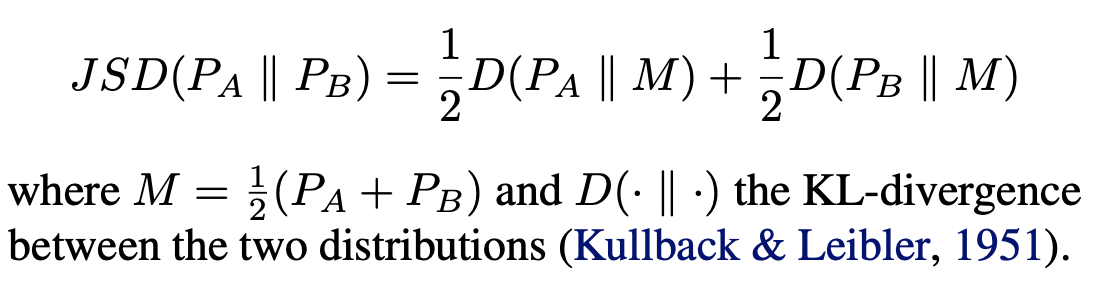
2) Coverage

• For each point cloud in A, first find its closest neighbor in B.
• Coverage is measured as the fraction of the point clouds in B that were matched to point clouds in A.
• Closeness can be computed using either the CD or EMD point-set distance.

3) Minimum Matching Distance(MMD)

• Coverage does not indicate exactly how well the covered point-clouds are represented in set A.
• Measure the fidelity of A with respect to B.
• Match every point cloud of B to the one in A with the MMD and report the average of distances in the matching.
• CD and EMD can be used, yielding MMD-CD and MMD-EMD

✅ The set of point clouds A captures all modes of B with good fidelity when MMD is small and Coverage is large.

👾 Models for Representation and Generation

AutoEncoder, GAN which first trains an AE and then trains a minimal GAN in the AE's latent space.

1. Learning representations of 3D point clouds

• Input to AE network: point cloud with 2048 points (2048 x 3 matrix), representing a 3D shape.
• Encoder architecture follows the design principle of PointNet
• Encodes every point independently

• "Symmetric", permutation invariant function (e.g. a max pool) is placed after the convolutions to produce a joint representation.
• The output of the last convolutional layer is passed to a feature-wise maximum to produce a k-dimensional vector which is the basis for out latent space.

• Decoder transforms latent vector using 3 fully connected layers.

• For permutation invariant objective, EMD and CD are explored as losses.

2. Generative models for Point Clouds

Raw point cloud GAN (r-GAN)

• input: raw 2048 X 3 point set input.
• discriminator's architecture is identical to the AE, without any batch-norm and with leaky ReLUs.

Latent-space GAN (l-GAN)

• instead of raw point cloud input, data through a pre-trained autoencoder, which is trained separately for each object class with the EMD or CD loss function is passed.
• Both generator and discriminator of l-GAN then operate on the bottlenetck variables of the AE.
• Once training of GAN is over, convert a code learned by the generator into a point cloud by using the AE's decoder

3. Gaussian mixture model

• Gaussian Mixture Mode(GMMs) are fitted on the latent spaces learned by AEs.

👨🏻‍🔬 Experimental Evaluation

Representational power of the AE

Generalization ability

• Fig 1 showing AEs to encode unseen samples from the test split (left) and then decode them and compare them visually to the input (right)
  

Latent space and linearity

• Reulsts below attest to the smoothness of the learned space, but also highlight the intrinsic capacity of point clouds to be smoothly morphed.

• Fig 2 shows linear interpolations, in the latent space, between the left and right-most geometrics.

• Fig 3 shows altering the input geometry(left) by adding, in latent space, the mean vector of geometries with a certain characteristics (e.g., convertible cars or cups without handles).

Shape Completions

• Instead of feeding and reconstructing the same point cloud, It is possible to feed the network with an incomplete version of its expected output.
• Given proper training data, our network learns to complete severely partial point clouds.
  

Evaluating the generative models

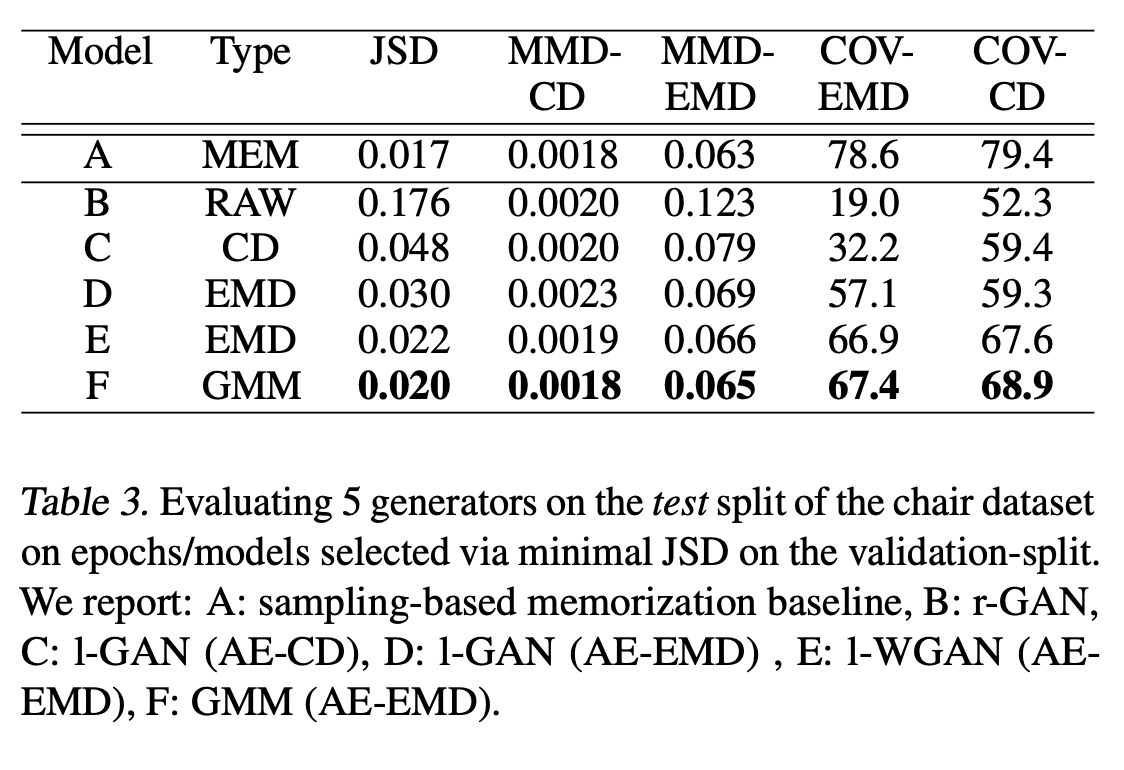
Comparison of paper's different generative models

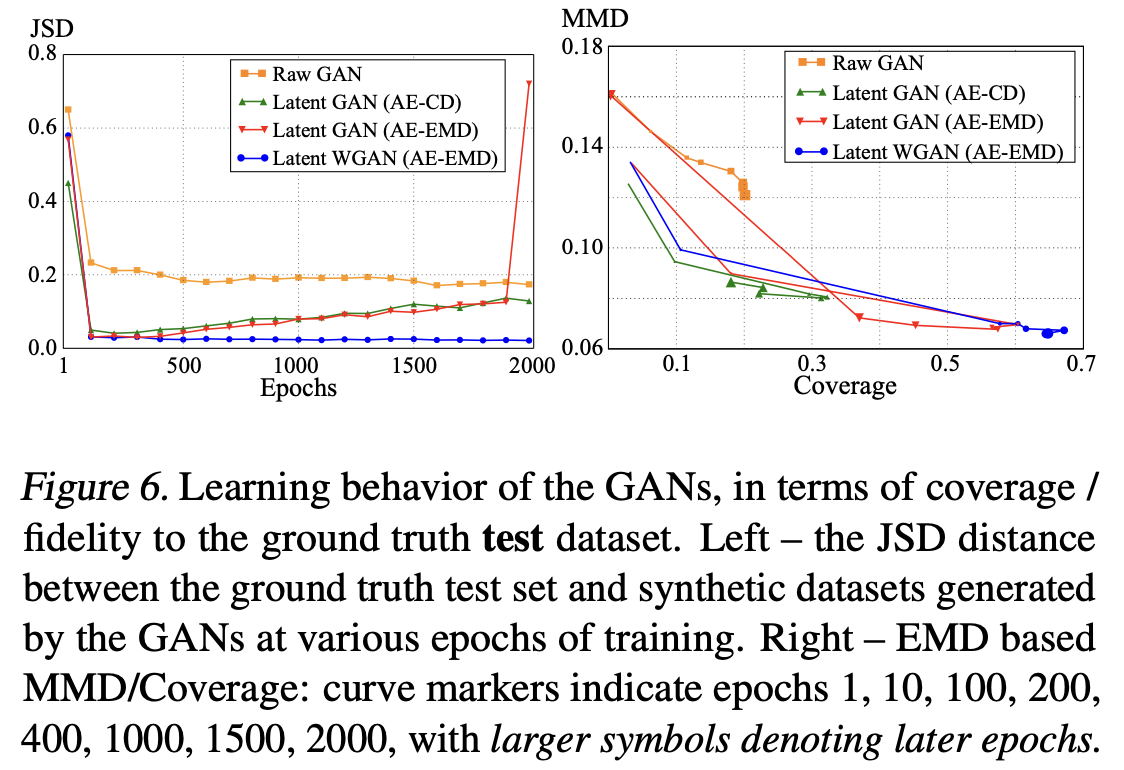
• r-GAN: struggles to provide good coverage and good fiedlity of the test set.
  (which alludse difficutly in training end-to-end GANs)

• l-GAN (AE-CD): performs better in fidelit with much less training, but its coverage remains low.

• EMD based AE(l-GAN, AE-EMD): dramatic improvement in coverage and fidelity.

• Both l-GANs suffer from mode collapse: half-way through training, dropping with fidelity which implies overfiiting a small subset of the data, and catastrophic collapse.

• Latent WGAN: largely eliminsates this collapse.
  

• Table 3 shows measurements for all generators based on the epoch that has minimal JSD between the generated samples and the validation set.

• Shows superioirity of the latent-based approaches and relative gains of using an AE-EMD vs. an AE-CD.
  -Demonstrates simple GMM can achieve results of comparable quality to a latent WGAN.

✅ Conclusion

• This paper's results show good generalization to unseen data and paper's representations encode meaningful semantics.
• Paper's Generative models produces faithful samples and cover most of the ground truth distribution.
• Experiments show the best generative model for point clouds is a GMM trained in the fixed latent space of an AE.