🚀 Motivations

• State-of-the-art deep neural networks are designed specifically to handle the irregularity of point clouds, directly manipulating raw point cloud data rather than passing to an intermediate regular representation.

• This approach was pioneered by PointNet which achieves permutation invariance of points by operating on each point independently and subsequently applying a symmetirc function to accumulate features.

• Various extensions of PointNet consider neighborhoods of points rather than acting on each independently. These allow the network to explot local features, improving upon performance of the basic model.

This techniques largely treat points independently at local scale to maintain permutation invariance. This independence, however, neglects the geometric relationships among points, presenting a fundamental limitation that cannot capture local features.

• ✅ To address these drawbacks, This paper propose a novel simple operation, called EdgeConv.

🔑 Key Contribution

• EdgeConv learning from clouds better captures local geometric features of point clouds while maintaining permutation invariance.

Instead of generating point features directly from their embeddings, EdgeConv generates edge features that "describe the relationships between a point and its neighbors".

It is designed to be invariant to the ordering of neighbors, and thus is permutation invariance. Because EdgeConv explicitly constructs a local graph and learns the embedding for the edges, the model is capable of grouping points both in Euclidean space and in semantic space.

• Model can leran to semantically group points by dynamically updating a graph of relationships from layer to layer.

• EdgeConv can be integrated into multiple existing pipelines for point cloud processing.

⭐ Methods

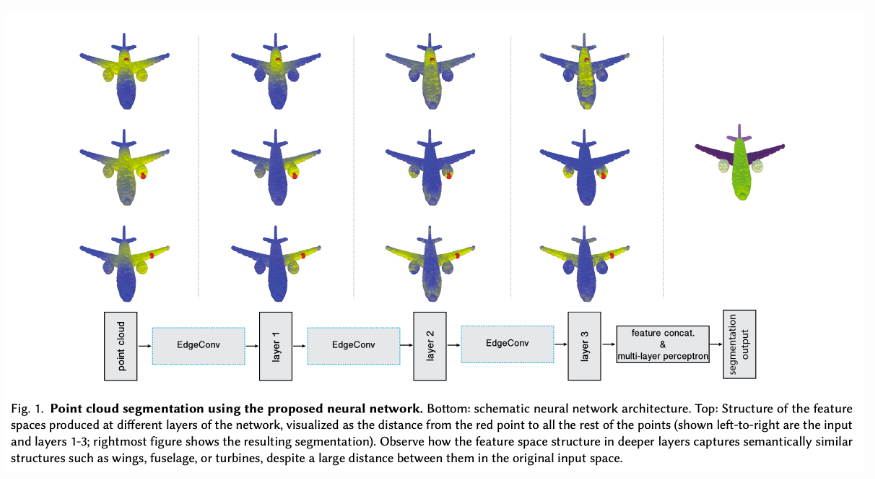
• This paper proposes an approach inspired by PointNet and convolution operations.

• It exploits local geometric structures by constructing a local neighborhood graph and applying convolution-like operations on the edges connecting neighboring paris of points. (Instead of working on individual points like PointNet)

• Graph is not fixed, Graph is dynamically updated after each layer of the network.
  Set of k-nearest neighbors of a point changes from layer to layer of the network
  and is computed from the sequence of embeddings.

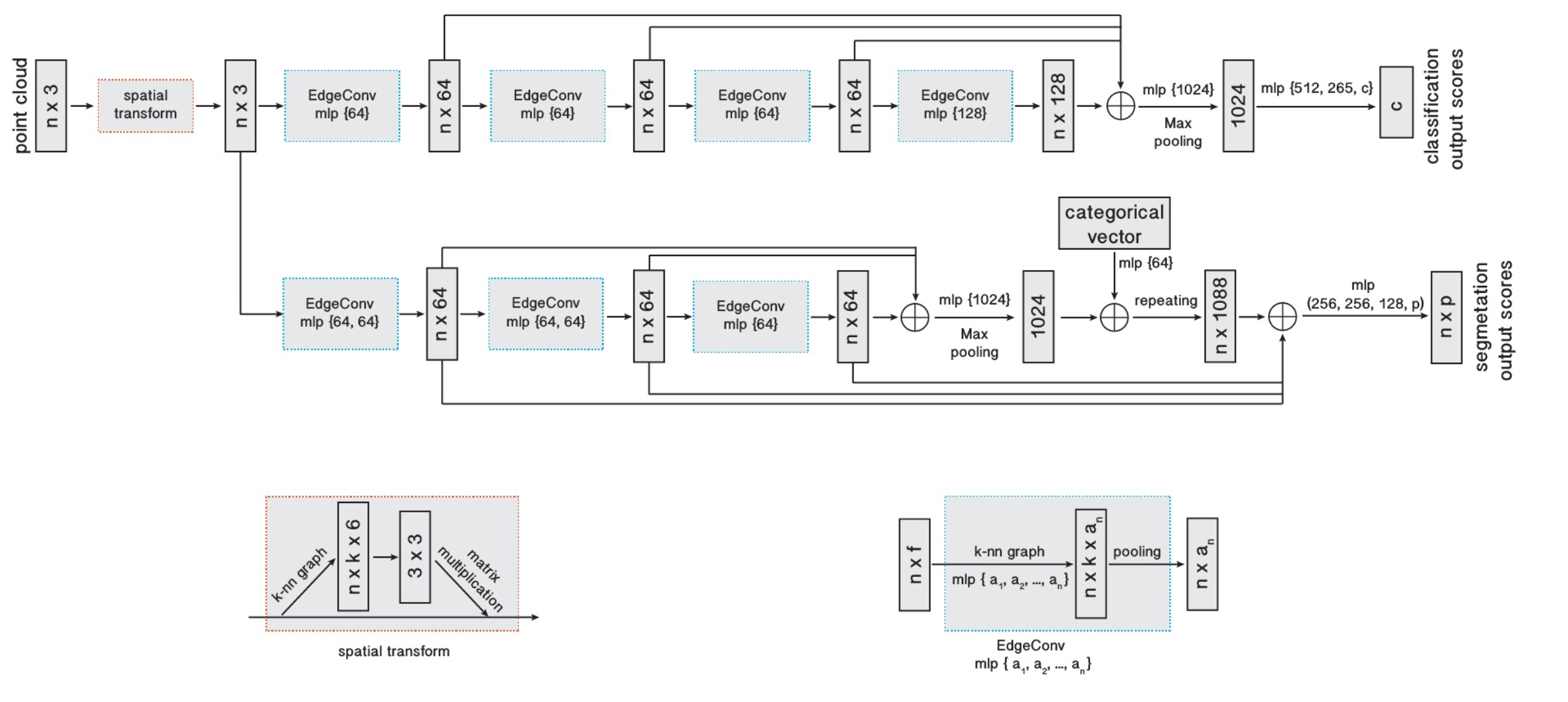
Edge Convolution

• F -dimensional point cloud with n points, denoted by X = {x1, . . . , xn } ⊆ R^F
  In the simplest setting of F = 3, each point contains 3D coordinates xi =(xi,yi,zi)
  Each subsequent layer operates on the output of previous layer.

• compute a directed graph G = (V, E) representing local point
  cloud structure, where V = {1,...,n} and E ⊆ V × V are the
  vertices and edges, respectively.

• edge features as eij = hΘ(xi,xj), where hΘ is a nonlinear function with a set of learnable parameters Θ.

• define the EdgeConv operation by applying a channel-wise symmetric aggregation operation □ (e.g., ∑ or max) on the edge features associated with all the edges emanating from each vertex.

• output of EdgeConv at the i-th vertex is thus given by
  

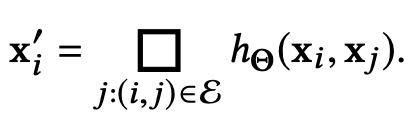
• Making analogy to convolution along images,
  we regard xi as the central pixel and {xj : (i,j) ∈ Ɛ } as a patch around it (see Fig2).

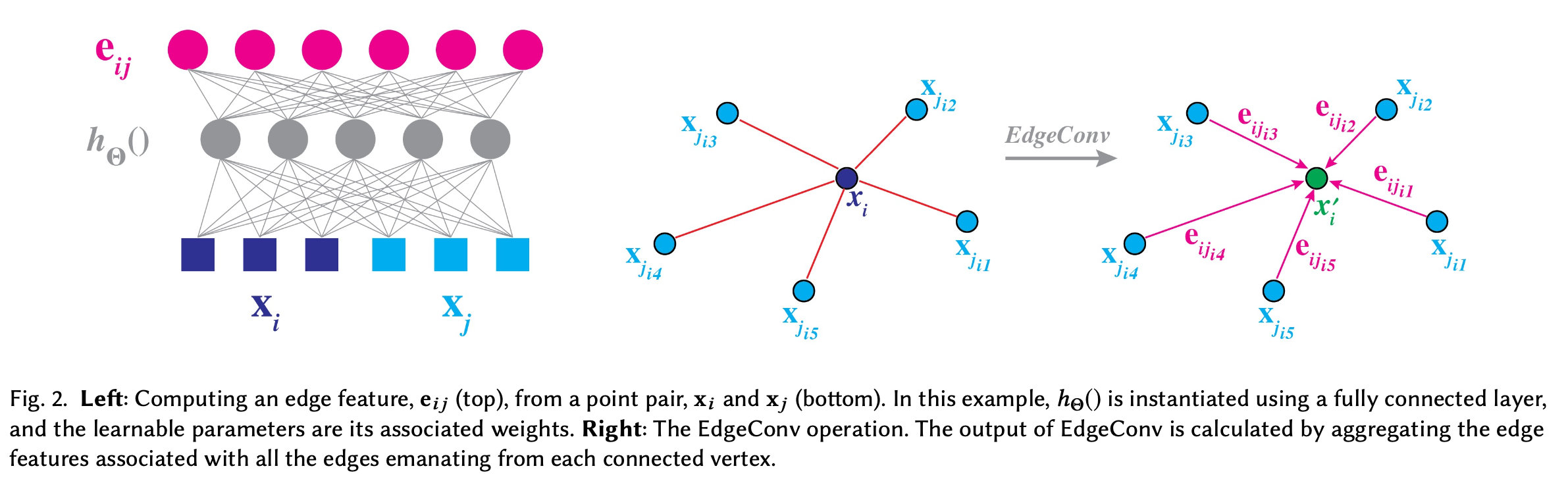
Dynamic Graph Update

This paper suggest Dynamic Graph CNN(DGCNN) that it is beneficial to recompute the graph using nearest neighbors in the feature space produced by each layer.

At each layer, it has a different graph

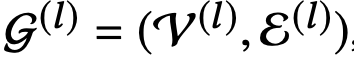
where l-th layer edges are the form

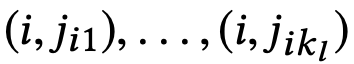
such that

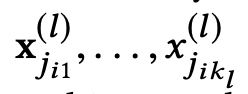
are the kl points closest to xi^(l)

This paper compute a pairwise distance matrix in feature space and take the closest k points for each single point.

Properties

1) Permutation Invariance

2) Translation Invariance

This operator has partial translation invariance property.
Part of the edge feature is preserved when shifting by T.

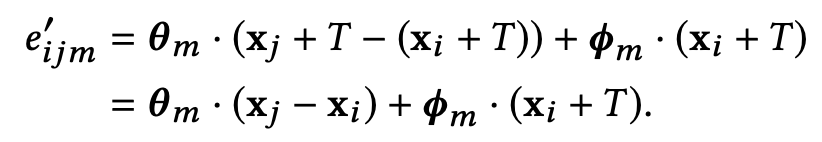
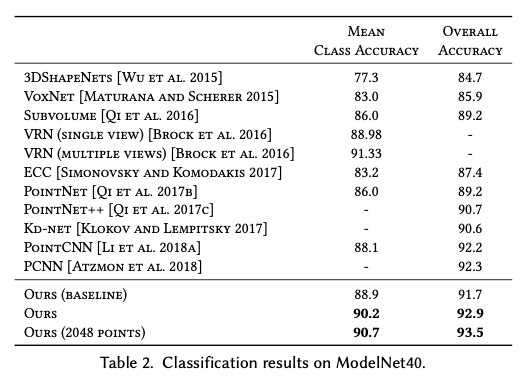
👨🏻‍🔬 Experiment Results

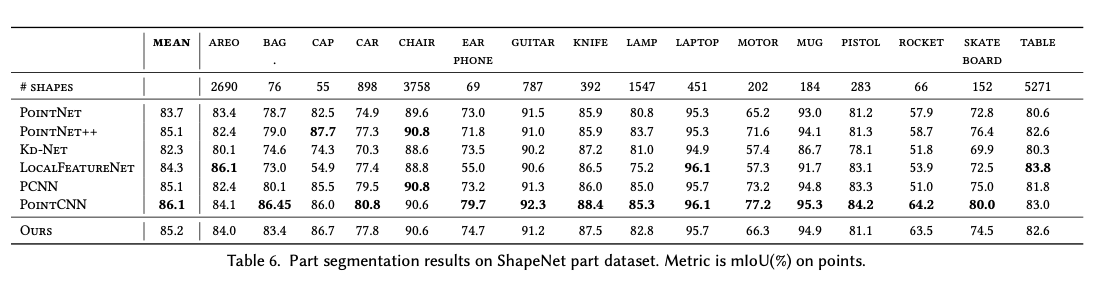
✏️ Limitations

• Very slow!
  Nearest neighbor search in a high-dimentional space requires a more delicate algorithm.
  

✅ Conclusion

• This model suggests that local geometric features are important to 3D recognition tasks, even after introducing machinery from deep learning.

• This paper proposes EdgeConv suitable for CNN-based high-levl tasks on point clouds including classification and segmentation.

• EdgeConv acts on graphs dynaically computed in each layer of the network.

• 1) EdgeConv incorporates local neighborhood information.
  2) it can be stacked applied to learn global shape properties
  3) in multi-layer systems affinity in feature space captures semantic characteristics over potentially long distances in the original embedding.