🚀 Motivations

• PointNet does not capture local structures induced by the metric space points live in, limiting its ability to recognize fine-grained patterns and generalizability to complex scenes.

• Thus, PointNet++ can be viewed as an extension of PointNet with added hierarchical structure.

🔑 Key Contribution

• PointNet++ leverages neighborhoods at multiple scales to achieve both robustnetss and detail capture.

• Network learns to adaptively weight patterns detected at different scales and combine multi-scale features according to the input data.

• PointNet++ is able to learn features even in non-uniformly sampled point sets.

🤔 Problem Statement

• Suppose X = (M, d) as discrete metric space, Where M is the set of points and d is th dinstance metric.

• This Paper is interested in learning set functions f that take such X as the input and produce information of semantic interest regarding X.

• In practice, such f can be classification function that assigns a label to x or a segmentation function that assigns a per point label to each member of M.

⭐ Methods

Extension of PointNet with Hierarchical Structure

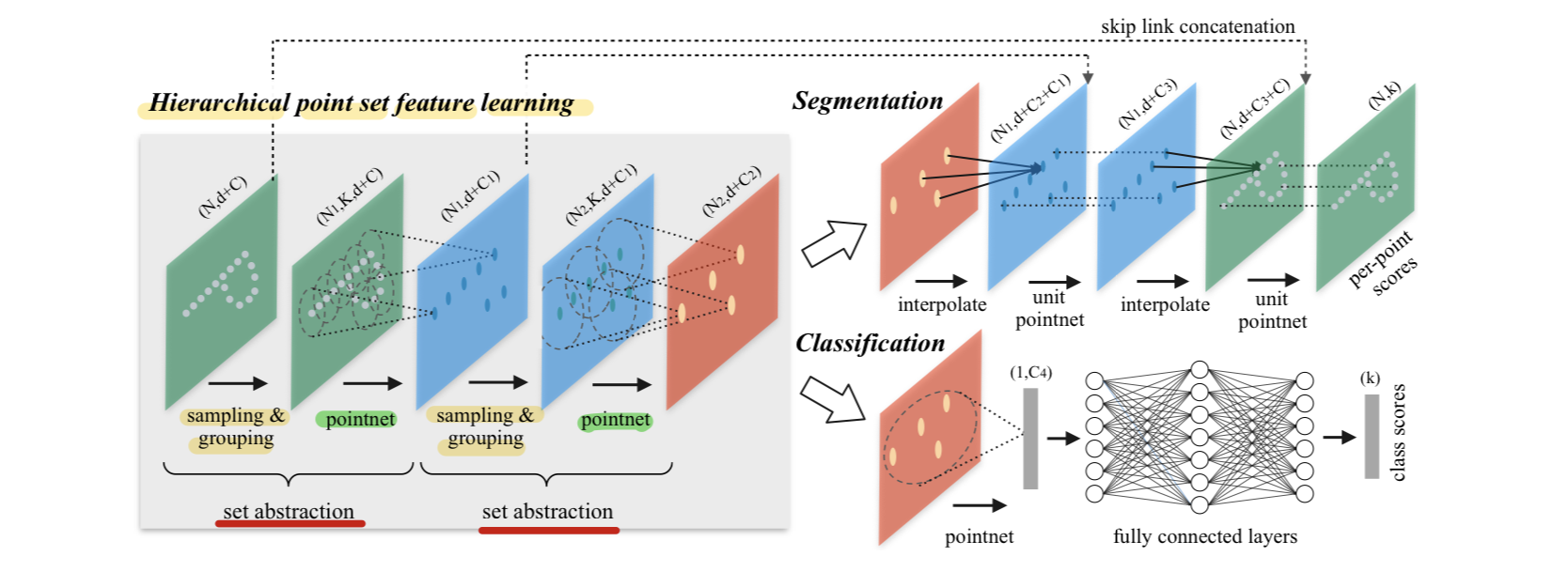
• While PointNet uses a single max pooling operation to aggregate the whole point set,
  this architecture builds a hierarchical grouping of points,
  and progressively abstract larger and larger local regions along the hierarchy.

• Hierarchical structure is composed by a number of set abstraction levels.
  At each level, a set of points is processed and abstracted to produce a new set with fewer elements.

• set abstraction level is made of 3 key layers:
  1) Sampling layer,
  2) Grouping layer and
  3) PointNet layer.

Set Abstraction Layer

• Sampling layer: Selecets a set of points from input points, which defines the centroids of local regions.

• Grouping layer: then constructs local region sets by finding "neighboring" points around the centroids.

• PointNet layer: uses a mini-PointNet to encode region patterns into feature vectors.

• input: N x (d + C) matrix
  from N points, with d-dim coordinates, and C-dim point feature.

• output: N' x (d + C') matrix
  N' subsampled points, with d-dim coordinates, and new C'-dim feature vectors summarizing local context.

Details of Set Abstraction Layer

• Sampling layer: Farthest Point Sampling(FPS)
  Given input points {x1, x2, ..., xn},
  this layer use iterative farthes point sampling(FPS) to choose a subset of points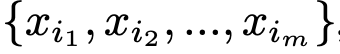 , such that xij is the most distant point (in metric distance) from the set {xi1, xi2, ... ,xi(j-1)} with regard to the rest points.
  Performacne: better coverage of the entire point set given the same number of centroids, Compared with random sampling.

• Grouping layer: Radius-based ball query
  -input: a point set of size N x (d+ C), coordinates of a set of centroids of size (N' x d)
  -output: groups of point sets of size N' x K x (d + C),
  where each group correspoinds to a local region and K is the number of point in the neighborhood of centroid points.

• PointNet layer
  This paper uses PointNet as the basic building block for local pattern learning.
  By using relative coordinatees together with point features, it can capture point-to-point relations in the local region.
  -input: N' local regions of points with data size N' x K x (d + C)
  -output: Each local region in the output is abstracted by its centroid and local feature that encodes the centriod's neighborhood. data size is N' x (d + C')

PointNet++: Robust Feature Learning under Non-Uniform Sampling Density

Challenge for point set feature learning

• It is common that a point set with non-uniform density in different areas.
• Non-uniformity introduces a significant challenge for point set feature learning.
• Features learned in dense data may not generalize to sparsely sampled regions.
  Consequently, models trained for sparse point cloud may not recognize fine-grained local structures.

Solution of this Paper

• What it want is to inspect as closely as possible into a point set to capture fines details in densely sampled regions.
• However, such close inspect is prohibited at low density areas, because local patterns may be corrupted by the sampling deficieny.
  In this case, looking for larger scale patterns in greater vicinicty is needed.
• This paper propose density adaptive PointNet layers that learn to combine features from regions of different scales, when the input sampling density changes.
  This Hierarchical network with density adaptive PointNet layer is PointNet++.

• This paper covered that each abstraction level contains grouping and feature extraction of a single scale above.
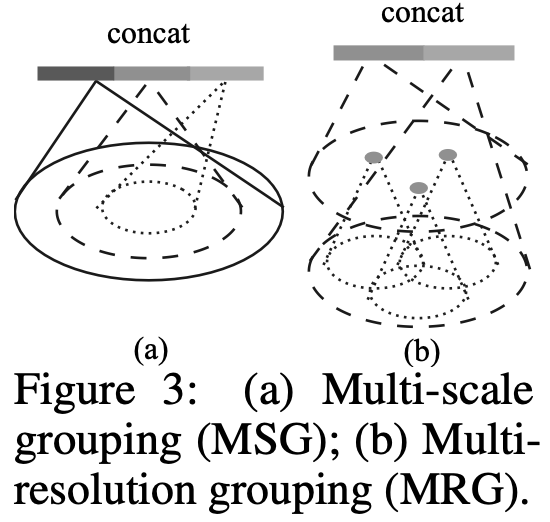
  In PointNet++, each abstraction level extracts multiple scales of local patterns and combine them according to local point densities.
• This paper propose two types of density adaptive layers in terms of grouping local regions and combining featurs from different scales.

1) Multi-scale grouping(MSG), Fig 3. (a)

• To apply grouping layers with different scales (followed by according PointNets to extract feature of each scale) is simple but effective way to capture multi-scale patterns.
• Features at different scales are concatenated to form a multi-scale feature.
• Randomly removes some of the input point cloud to simulate scanning deficiency.
• Drawback: Expensive! Need to run PointNet multiple times.

2) Multi-resolution grouping(MRG), Fig 3. (b)

• Another solution, Running PointNet only twice.
• Concatenate two features
• MSG approach is computationally expnsive, since it runs local PointNet at large scale neighborhoods for every centroid point.
  (In particulary, at the lowest level, large number of centroid points make time cost significant.)
• MRG is an alternative approach for avoiding expensive computation, but still adaptively aggregate info according to the distributional properties of points.
• features of a region at same level Li, is a concatenation of two vectors.
• Left: Integrates keypoint fetures learned in the previous set abstration layer.
  (Like vanilla PointNet++)
  (Useful when the points are dense enough in the region.)
• Right: Integrate raw point coordinates.
  (Like the first layer of PointNet)
  (More robust with sparse points)
• Compared with MSG, MRG is computationally more efficient since we avoids the feature extraction in large scale neighborhoods at lowest levels.

👨🏻‍🔬 Experiments Results

Robust learning under varying sampling density

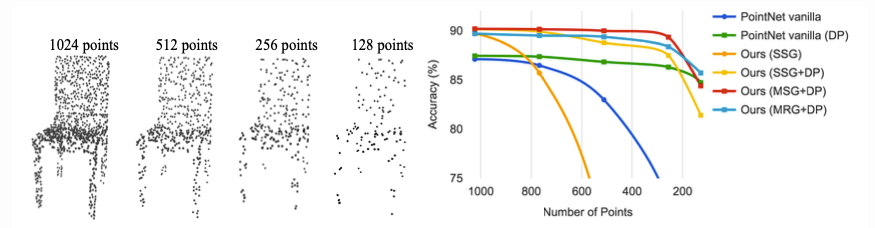
Classification performance comparison

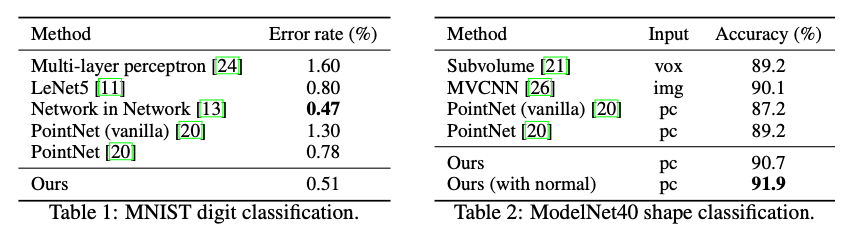
✏️ Limitations

• PointNet++ consider neighborhoods of points rather than acting on each independently. It allows the network to exploit local feature, improving upon performance of the basic mode.
• This techniques largely treat points independently at local scale to maintian permutation invariance.
• This independence, however, neglects the geometric relationships among points, presenting a fundamental limitation that cannot capture local features.
  ➡️ Motivation of Dynamic Graph CNN for Learning on Point Cloud

✅ Conclusion

• This paper propses PointNet++ for processing point sets sampled in a metric space.

• It recursively functions on a nested partitioning of the input point set, and is effective in learning hierarchical features w.s.t the distance metric.

• To handle non uniform point sampling issue, This paper proposes two set abstraction layers that aggregate multi-scale information according to local point densities.