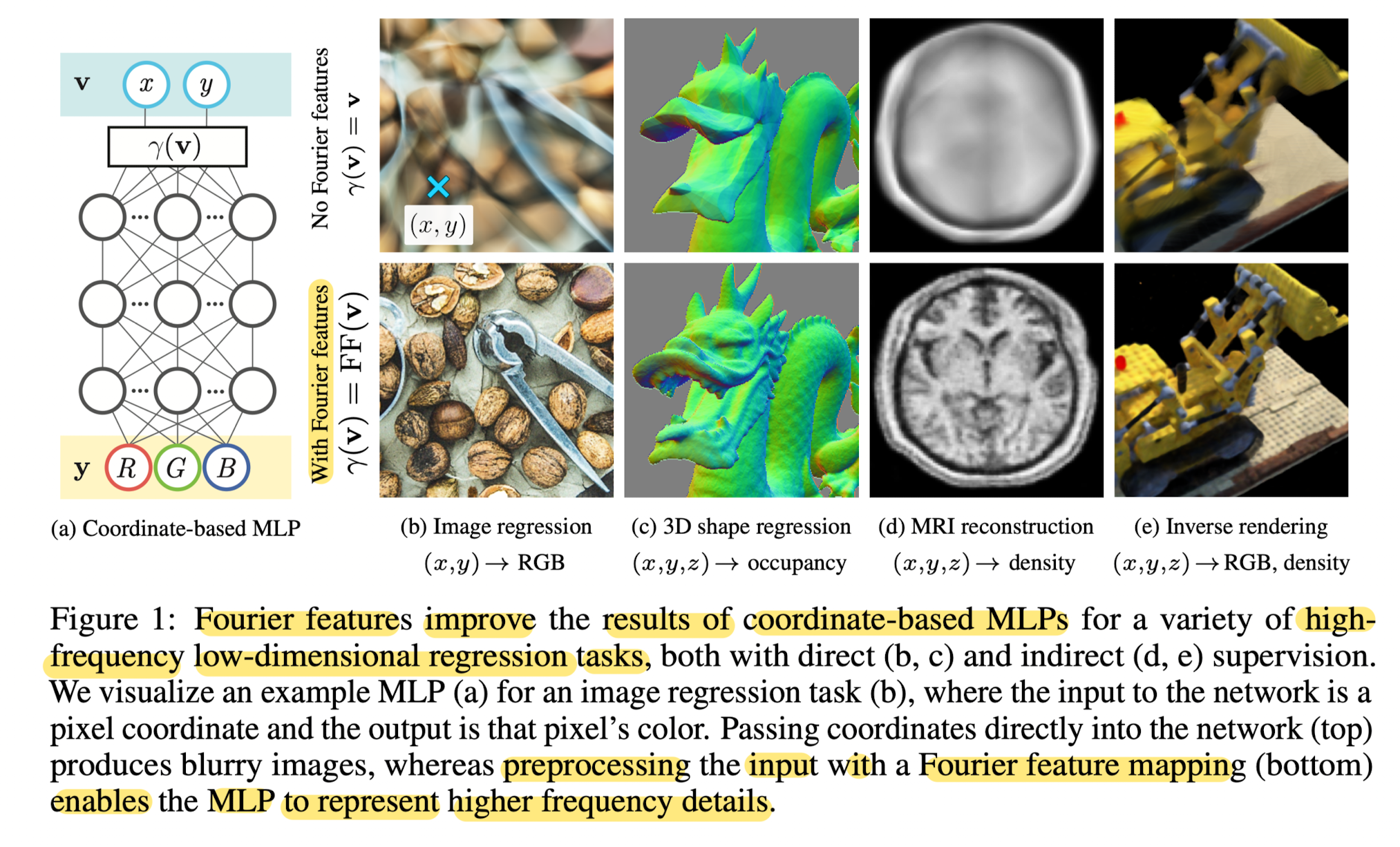
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
ML For 3D Data
🚀 Motivations
-
standard MLPs are poorly suited for low-dimensional coordinate-based vision and graphic tasks.
-
MLPs have difficulty learning high frequency functions referred as "spectral bias"
: NTK(Neural Tangent Kernel) theory suggests that this is beacuse standard coordinate-based MLPs correspond to kernels with a rapid frequency falloff,
which prevents them from being able to represent the high-frequency content present in naural images and scenes.
🔑 Key contributions
-
This paper leverage NTK theory and simple experimetns to show that a Fourier feature mapping can be used to overcome the spectral bias of coordinate-based MLPs towards low frequencies by allowing them to learn much higher frequencies.
-
This paper demonstrates that arandom Fourier feature mappin with an appropriately chosen scale can dramatically improve the performan cof coordinate-based MLPs across many low-dimensional tasks in computer vision and graphics.
⭐ Fourier Features for a Tunable Stationary Neural Tangent Kernel
-
This paper considers low-dimensional regression tasks, wherein
inputs: assumed to be dense coordinates in a subset of ℝ^d for small values of d (e.g.pixel coordinates) -
Two signification implications when viewing deep networks through the lens of kernel regression
1) composed NTK to be shift-invariant over the input domain.
A Fourier feature mapping of input coordinates makes the composed NTK shift-invariant, acting as a convolution kernel over the input domian.
2) control the bandwidth of the NTK to improve training speed and generalization.
This paper shows Fourier feature input mapping can be tuned to lie between underfitting and overfitting extremes, enabling both fast convergence and low test error.
Fourier feature and the composed neural tangent kernel
- This paper uses a Fourier feature mapping γ to featurize input coordinates before passing them through a coordinate-based MLP.
- The function γ maps input points v ∈ ㄷ0, 1) ^ d to the surface of a higher dimensional hypersphere with a set of sinusoids:

- After computing the Fourier feature for input points, pass them through an MLP to get f(γ(v); θ)
- The result of training a network can be approximated by kernel regression using the kernel
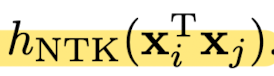


- This allows to draw analogies to signal processing, where the compesed NTK acts similarly to a reconstruction filter.
🌟 Manipulating the Fourier Feature Mapping
- Perprocessing the inputs to a coordinate-based MLP with a Fourier feature mapping creates a composed NTK that is not only stationary but also tunable.
- By manipulating the settings of the aj and bj parameter in Eqn.5,
it is possible to dramatically change both the rate of convergence and the generalization behavior of the resulting network.
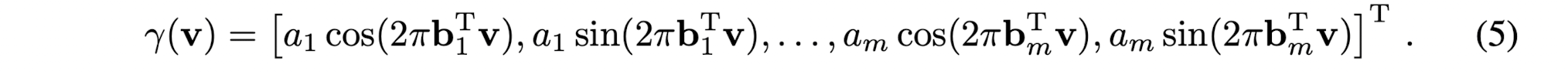
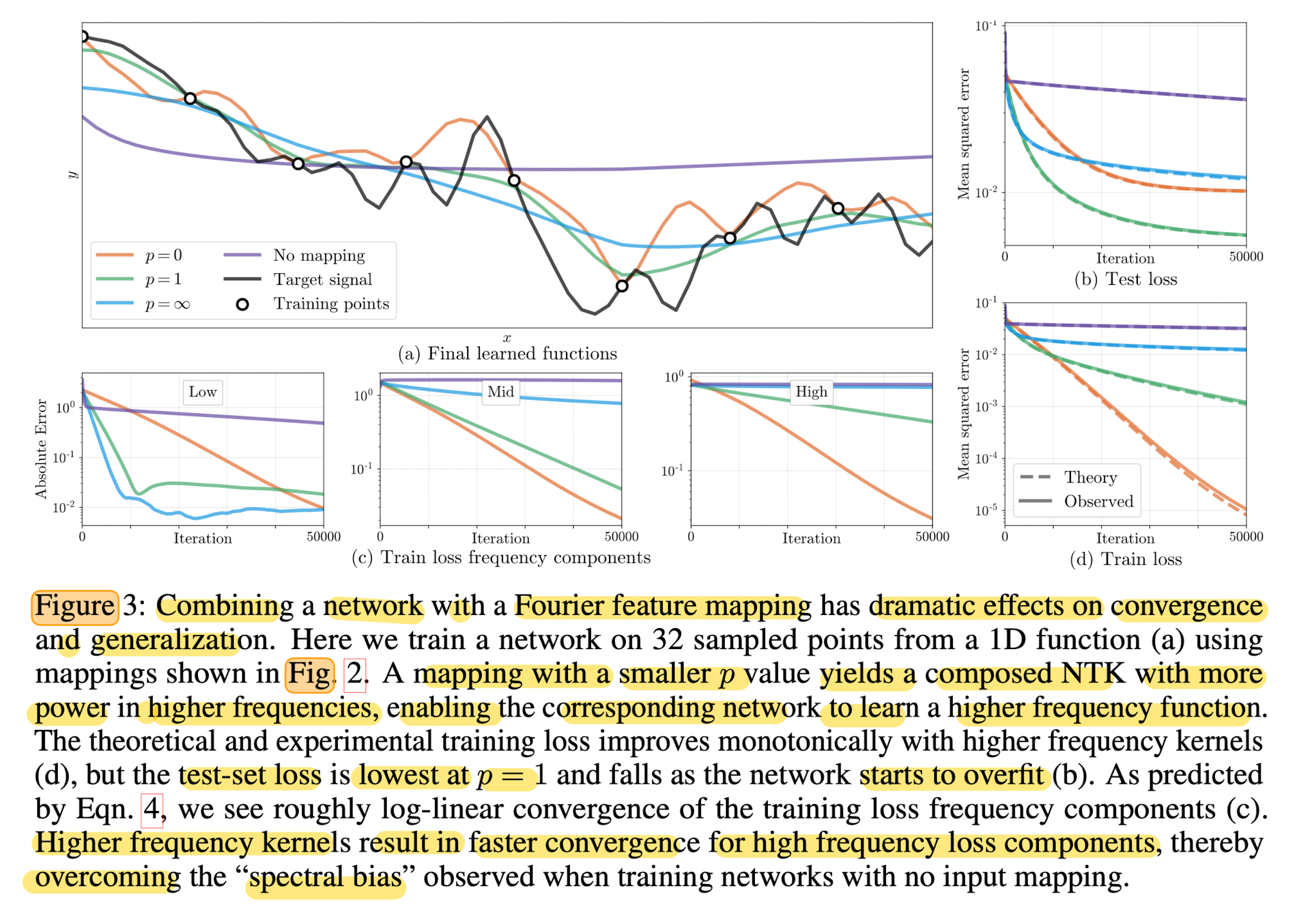
Effects of Fourier feature on network convergence
- Fig 3b & 3d: show that NTK linear dynamics model accurately precict the effects of modifying the Fourier feature mapping aprameters.
- Fig 3c:
1) networks with narrower NTK spectra converge faster for low frequency components, but never converge for high frequency components.
2) networks with wider NTK spectra converge across all components.
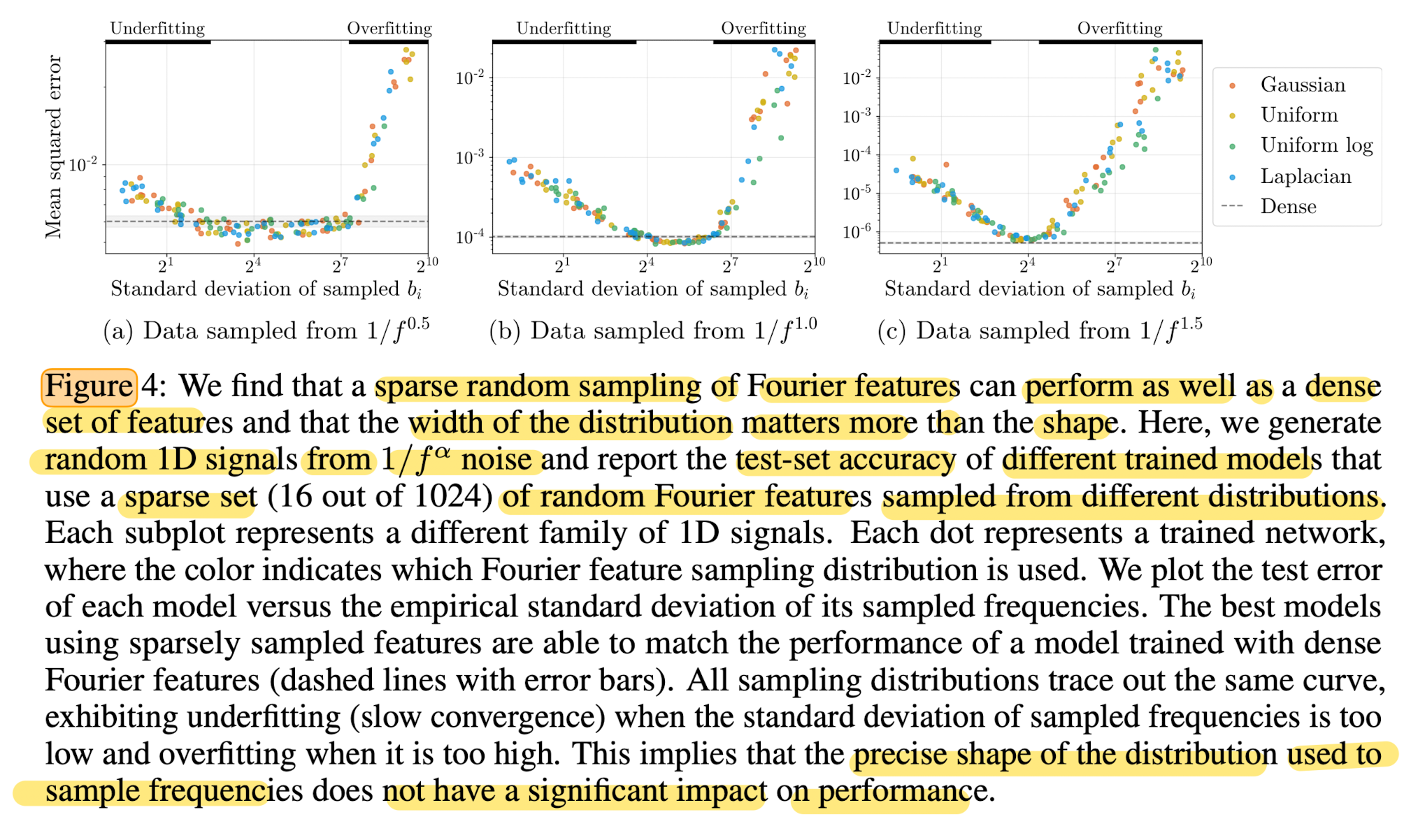
Tuning Fourier features in practice
👨🏻🔬 Experimental Results
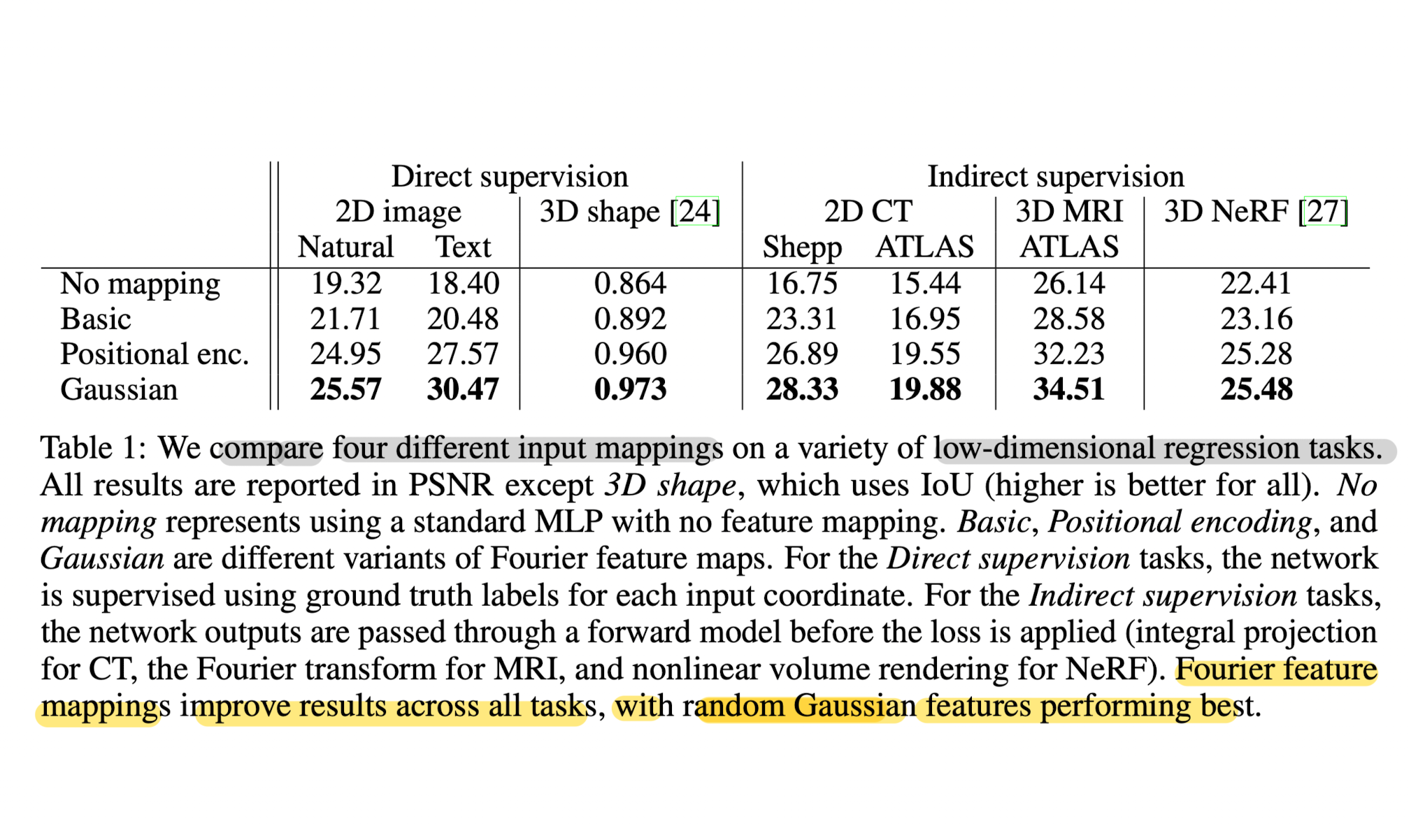
- For further details, please refer to experimental details of this paper.
✅ Conclusions
-
This paper leverages NTK theory to show that a Fourier feature mapping can make coordinate0based MLPs better suited for modeling functions in low dimensions, therby overcoming th espectral bias inherent in coordinate-based MLPs.
-
Experimentally show that tuning the Fouriere feature parameters offers control over the frequency falloff of the combined NTK and improves performance across a range of graphics and imaging tasks.