🚀 Motivations
-
Current network architectures for such implicit neural representations are
1) incapable of modeling signals with fine detail,
2) fail to represent a signal's spatial and temporal derivatives,
despite these are essentail to physical signals as the solution to partial differential equations. -
Most of recent representations build on ReLU-based MLPs.
While promising,
1) lack the capacity to represnet fine details in the underlying signals
2) do not represent the derivatives of a target signal well
due to ReLU networks are piecewise linear, their second derivative is zero anywere, and thus incapable of modeling info contained in higher-order derivatives of natural signal.
While alternative activations, such as tanh or softplus, capable of representing higher-order deriv,
This paper demonstrated their deriv are not well behaved and fail to represent details.
➡️ This paper leverage MLPs with periodic activation functions for implicit representations, which is capable of representing details in the singals.
🔑 Key contributions
-
A continuous implicit neural representation using sine as periodic activation functions that fits complicated signals, such as natural images and 3D shapes, and their derivatives.
-
An initialization scheme for training these representations and
validation that distributions of these representations can be learned using hypernetworks. -
Demonstration of applications in: image, video, and audio representation;
3D shape reconstruction;
solving first-order differential equations that aim at estimating a signal by supervising only with its gradients;
and solving second-order differential equations.
⭐ Formulation
-
Goal: to solve problems of the form of a class of functions Φ that satisfy equations
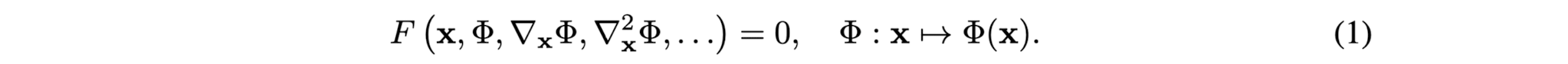
-
This implicit problem formulation's
-input: spatial or spatio-temporal coordinates x ∈ ℝ^m and optionally, derivatives of Φ w.r.t theses coordinates.
-goal: to learn a NN that parameterizes Φ to map x.
-Φ is implicitly defined by the relation defined by F and this paper refer to neural NN that parametrizes such implicitly defined functions as implicit neural representations. -
This paper cast this goal as a feasibility problem,
where a function Φ is sought that satisfies a set of M constraints
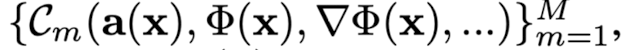
each of which relate the function Φ and/or its derivatives to quantities a(x):
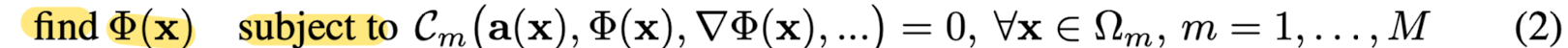
-
This problem be cast in a loss function that penalizes deviations from each of the constraints on their domain Ωm:
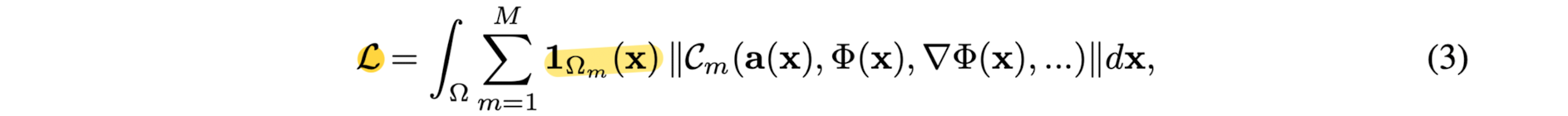
with the indicator function
1Ωm = 1 when x ∈ Ωm
1Ωm = 0 when x ∉ Ωm -
This paper parameterize functions Φθ as FCNN with parameters θ,
and solve the resulting optimization problem using gradient descent.
Periodic Activations for Implicit Neural Representations
-
This paper proposes SIREN, a simple NN architeucture for implicit neural representations that uses the sine as a periodic activation function:

-
Any derivative of a SIREN is itself a SIREN, Therefore, the derivatives of a SIREN inherit the properites of SIRENs,
enabling to supervise any derivate of SIREN with complicated signals.
Simple example: fitting an image
-
case of finding the function Φ: ℝ^2 -> ℝ^3,
x -> Φ(x),
that parameterizes a given discrete image f. -
image defines a dataset D = {(xi, f(xi))} of pixel coordinates xi = (xi, yi).
-
This Only constraint C compels is that
Φ output image colors at pixel coordinstaes, soley depending on Φ(none of its deriv)
and f(xi), with the form C(f(xi), Φ(x)) = Φ(xi) - f(xi)
which can be translated into the loss below -
loss:
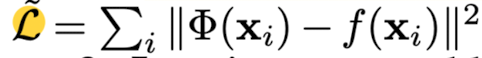
-
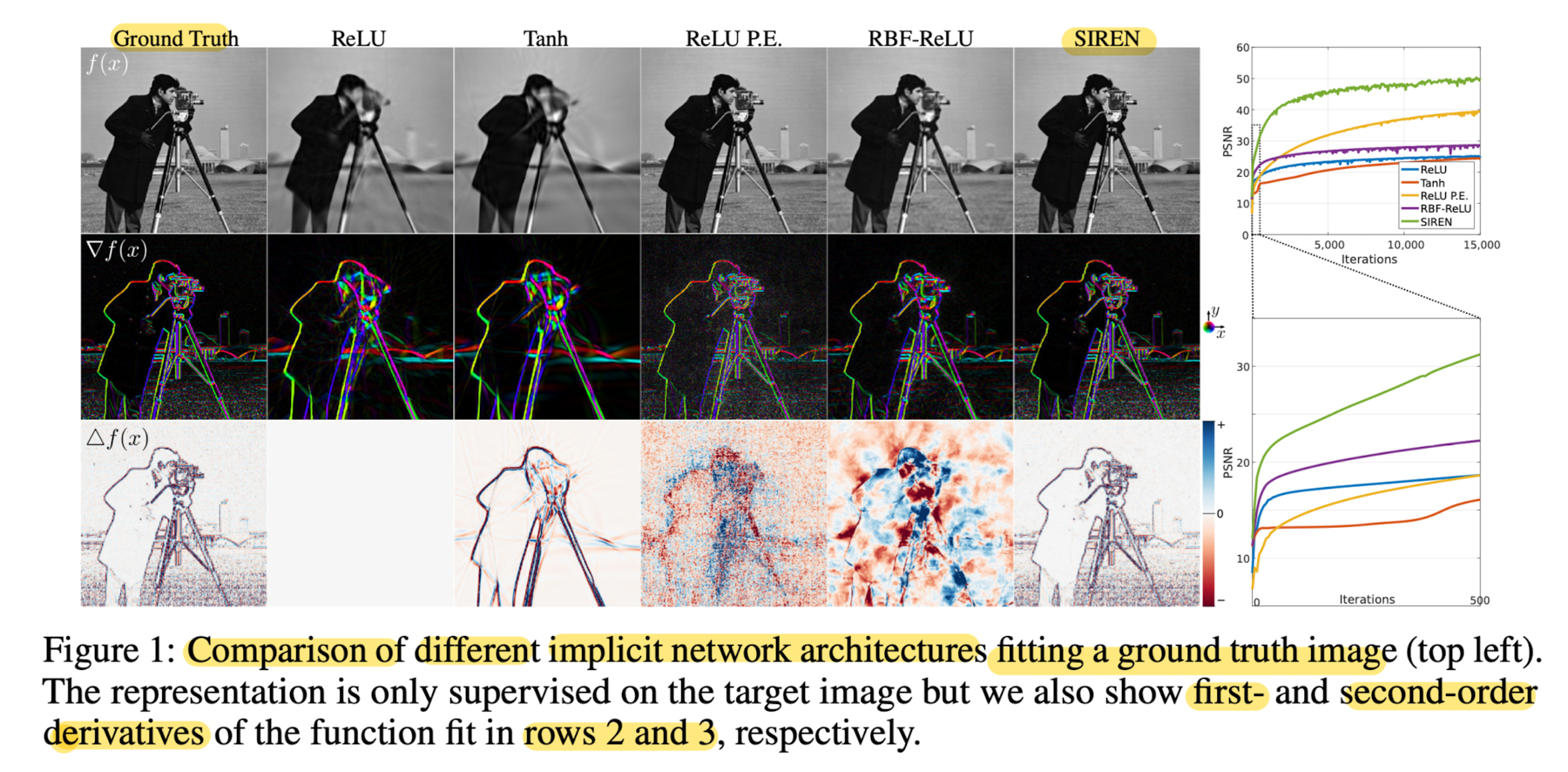
This paper fit Φθ using comparable network architectures with different activation functions to a natural image.
(RelU network with positional encoding and SIREN) -
Supervise this experiment on the image values,
also visualize the graidents ∇f and Laplacians ∆f. -
SIREN is the only network capavle of also representingg the derivative of the signal.
-
Fig 2 shows simple experiment, this paper fit a short video with 300 frames and with a resolution of 512 x 512 pixels
using both ReLU and SIREN MLPs. -
SIREN MLPs is successful in representing the video with an average peak signal-to-noise-ratio close to 30dB,
outperforming the ReLU baseline by about 5dB.

Distribution of activations, frequncies, and a principled initialization scheme
- This paper presents a pincipled initialization scheme necessary for the effective training of SIRENs.
- Key idea in initialization scheme is to preserve the distribution of activations through the network so that the final output at initialization does no depend on the number of layers.
- Please refer the paper of details.
👨🏻🔬 Experimental Results
Solving the Poisson Equation
- This paper demonstrated that the proposed representation accurately represent a function and its derivatives,
also can be supervised solely by its derivatives.

Poisson image reconstrunction
- Solving the Poisson equation enables the reconstruction of images from their derivatives.
- Supervising the implicit representaion with either GT gradients via Lgrad. or Laplacians via Llapl. successfully reconstructs the image.

Poisson image editing
- Imaes can be seamlessly fused in the gradient domain.
- Φ is supervised using Lgrad,
where ∇xf(x) is a composite function of the gradients of two images f1,2:
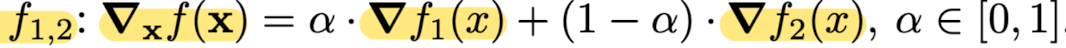
Representing Shapes with Signed Distance Functions
- This paper fit a SIREN to an oriented point cloud using a loss of the form
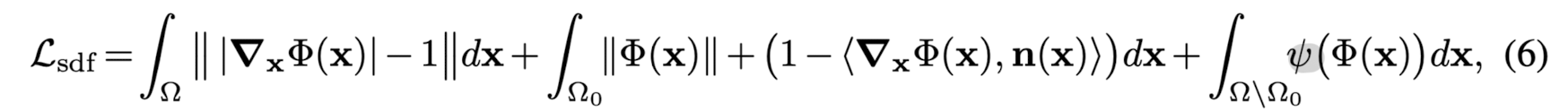

- The model Φ(x) is supervised using oriented points sampled on a mesh,
where thie paper require the SIREN to respect Φ(x) = 0 and its normals n(x) = ∇f(x) - During training, each minibatch contains an equal number of points on and off the mesh, each one randomly sampeld over Ω.

- Fig 4 shows the proposed periodic activations significantly increase the details of objects and the complexity of scenes that can be represented by these neural SDFs
parameterizing a full room with only a single five-layer FCNN. - This is in constrast to concurrent work that addresses the same failure of conventional MLP arch to represent complex or large scenes by
locally decoding a discrete representation, such as a voxelgrid, into an implicit neural representation of geometry.
- please refer to papers about solving the Helmholts and Wave Equations.
✅ Conclusion
- This paper demonstrates that periodic activation functions are ideally suited for representing complex natural signals and their derivatives using implicit neural representations.