🚀 Motivations
-
Unlike for images, in 3D there is no canonical representation which is both computationally and memory efficient yet allows for representing high-resolution geometry of arbitrary topology.
-
Many of the SOTA learning based 3D reconstruction approaches can only represent very coarse 3D geometry or are limited to a restricted domain.
-
While generative models have recently achieved remarkable successes in generating realistic high resolution images, this success has not yet been replicated in the 3D domain.
-
3D output representation is neither memory efficient nor be efficiently inferred fromdata.
➡️ This paper proposes an approach to 3D reconsturction based on directly learning the continuous 3D occupancy function. (Fig 1d)
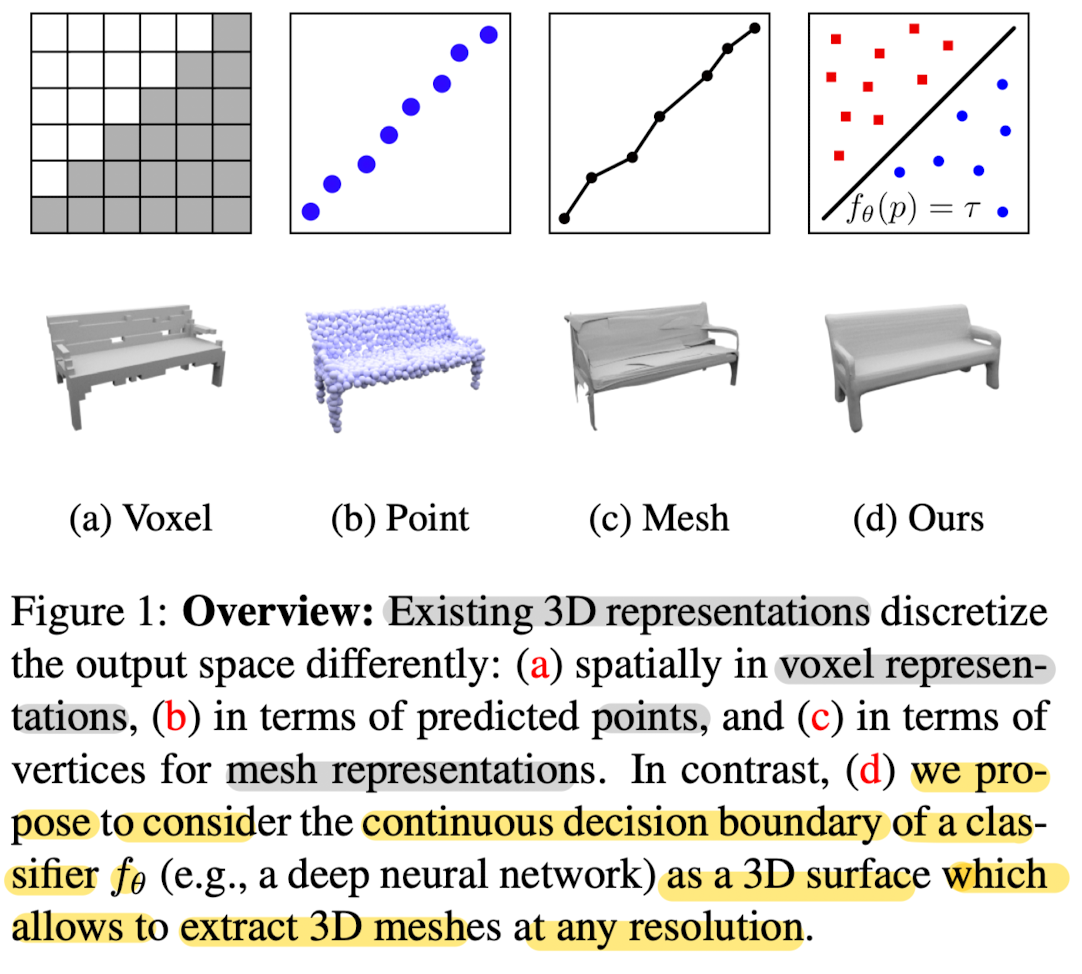
⭐ Methods
-
This paper proposes Occupancy Networks, a new representation for learning-based 3D reconstruction methods.
-
It implicitly represent the 3D surface as the continuous decision boundary of a deep neural network classifier.
-
In contrast to existing approaches, this representation encodes a description of the 3D ouput at infinite resolution without excessing memory footprint.
Occupancy Networks
-
Occupancy function: This paper calls Occupancy function which is a resulting function that reasons about the occupancy at every possible 3D point p ∈ R^3.
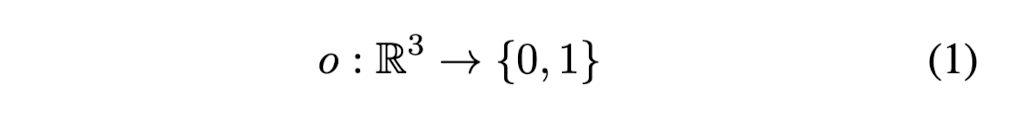
-
Key insight is that approximating this 3D function with a NN that assigns to every location p ∈ R^3 an occupancy probability between 0 and 1.
(Equivalent to a NN for binary classification, except being interested in the decision boundary which implicitly represents the object's surface.)
- Function that takes an obeservation x ∈ X as input,
and Function from p ∈ R^3 to R as output,
can be equivalently described by a function that takes a pair (p,x) ∈ R^3 x X as input, and outputs a real number. - The latter representation can be simply parameterized by a NN fθ that takes a pair (p,x) as input and outputs a real number which represents the probaility of occupancy.
- This is Occupancy Network.
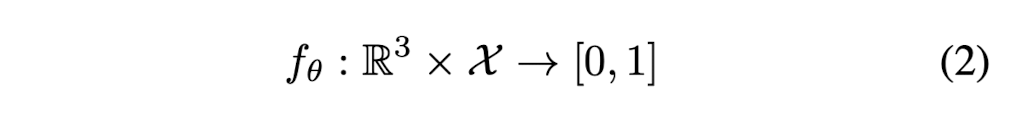
Training
Inference
-
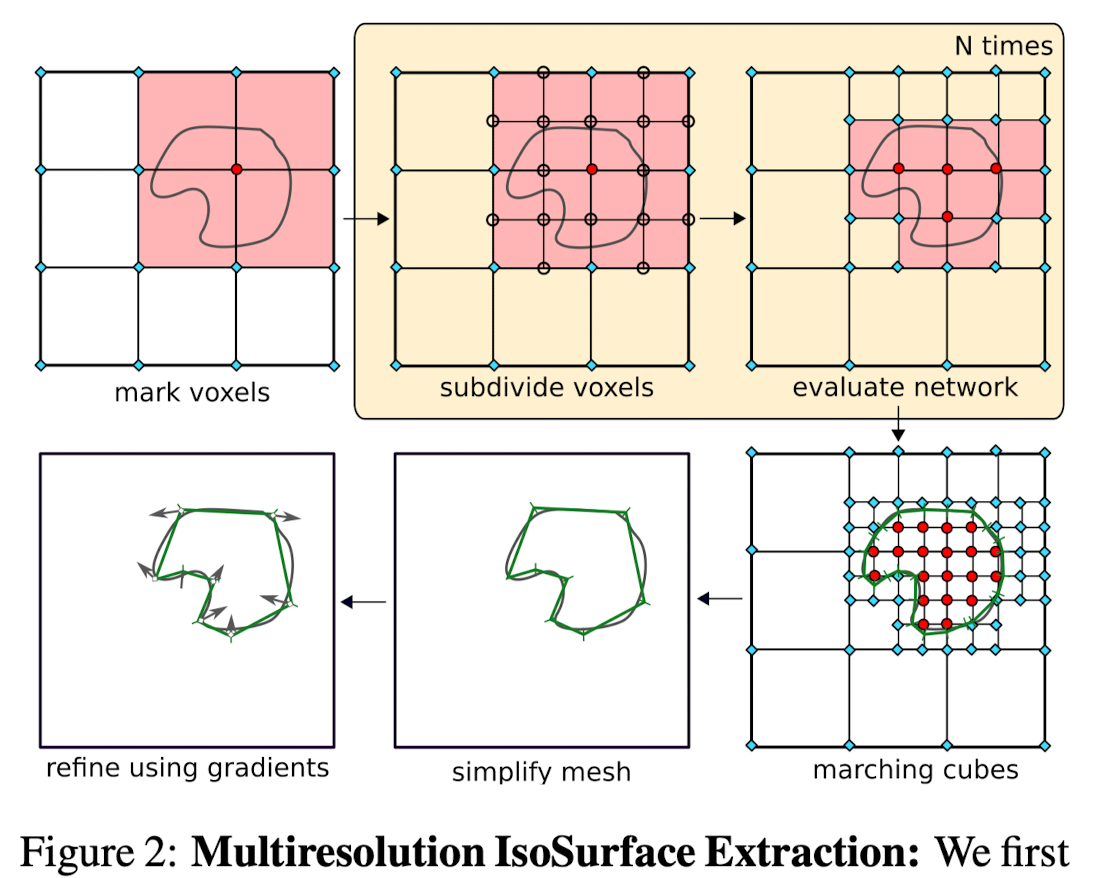
For extracting the isosurface corresponding to a new observation given a trained occupancy network, this paper introduces MISE(Multiresolution IsoSurface Extraction), a hierarchical isosurface extraction algorithm (Fig 2).
-
MISE enables to extract high resolution meshes from the occupancy network without densely evaluating all points of a high-dimensional occupancy grid.
-
- Discretize the volumetric space at an initial resolution
-
- Evaluate the occupancy network fθ(p,x) for all p in this grid.
-
- Mark all grid points p as occupied for which fθ(p,x) is bigger or equal to some threshold τ.
-
- Mark all voxels as active for which at least two adjacent grid points have differing occupancy predictions.
(These are the voxels which would intersect the mesh if marching cubes algorithm is applied at the current resolution.)
- Mark all voxels as active for which at least two adjacent grid points have differing occupancy predictions.
-
- Subdivide all active voxels into 8 subvoxels.
-
- Evaluate all new grid points which are introduced to the occupancy grid through this subdivision.
-
- Repeat these steps until the desired final resolution is reached.
-
- At this final resolution, algorithm converges to the correct mesh if the occupancy grid at the initial resolution contains points from every connected component of both the interior and the exterior of the mesh.
👨🏻🔬 Experimental Results
Metrics
- volumetric IoU, Chamfer-L1 distance, normal consistency score
Representation Power
-
Onet = Occupancy Network
-
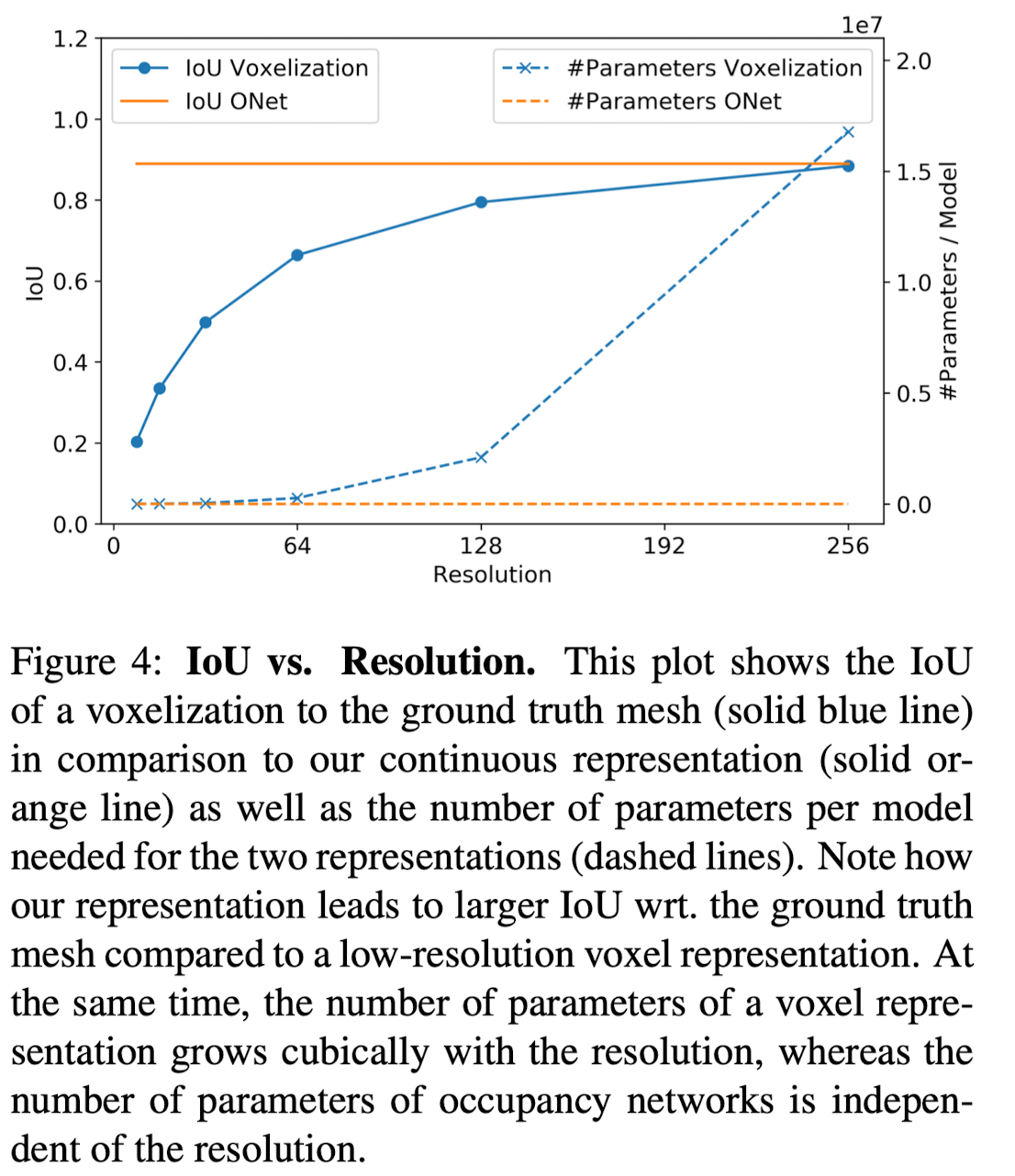
This paper measures the volumetric IoU to the ground truth mesh.
-
Onet represents high mean IoU of 9.89
(while a low-reolution voxel representation is not able to represent the meshes accurately.) -
Onet is able to encode all training samples with as little as 6M parameters, independently of the resolution.
(in contrast, memeory requirements of a voxel representation grow cubically with resolution.)
-
Occupancy network represents details of the 3D geometry which are lost in a low0resolution voexlization.

Single Image 3D Reconstruction
- Occupancy Network is able to capture complex topologies, produces closed meshes and preserves most of the details.
- For Further Details, please refer to this paper.

- Below Fig 6a shows how well ONet generalizes to real data.
- Method generalizes well to real images despite being trained soley on synthetic data.

- Please refer to this paper for Further Experiments Details.
✅ Conclusion
-
This paper introduced occupancy networks, a new representation for 3D geometry,
-
which is not constrained by the discretization of the 3D sapce and can hence be used to represent realistic high-resolution meshes.
-
This paper showed expressiveness and effectiveness of occupacny networks both for supervised and unsupervised learning through experiments.