GPTQ 논문

관련 논문
[핵심]Optimal Brain Quantizer

---

1. Greedy ➡️ Arbitrary Order

OBQ: 각 row마다 quantization error를 최소화하는 weight를 greedy하게 선택하고, quantization하는 방식을 사용한다.

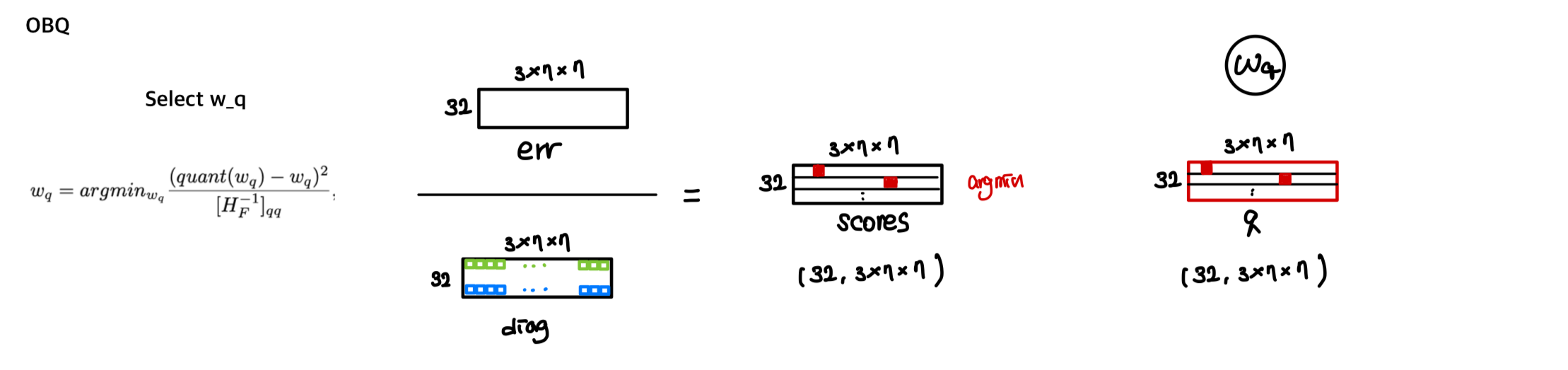
GPTQ: 모든 row를 동일하게(모든 row에서 동일한 column을) fixed order로 quantization 해도 결과에 큰 차이가 없더라. 이 방식이 연산량도 더 작다.

---

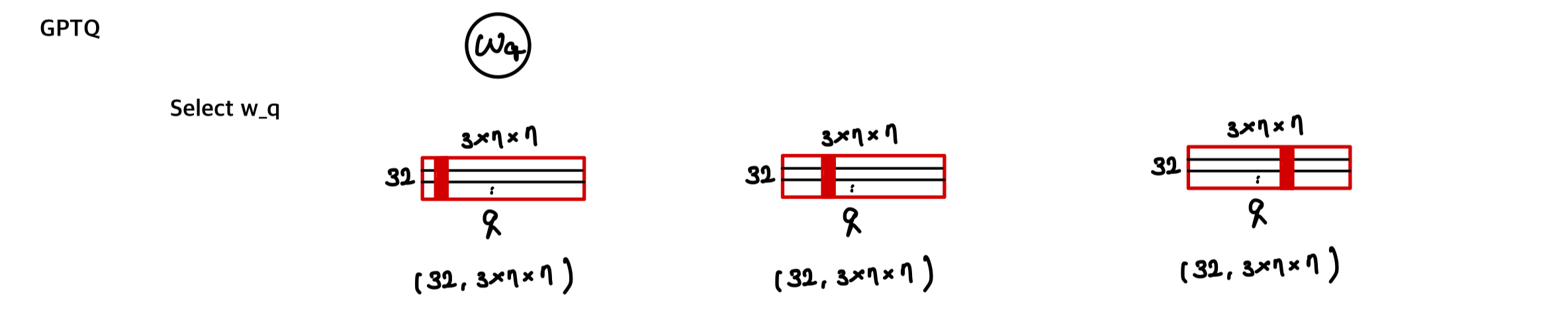
2. Lazy Batch-Updates

GPTQ: 여러 column들을 한 번에 처리하는 batch-update 방식을 도입했다.

$i$번째 column에 대한 최종 rounding decision은 오직 이 column에 대해 수행된 updates에만 영향을 받으므로, 이 시점에서 이후 column들에 대한 업데이트는 무관하다. 이를 통해 updates를 'lazily batch' updates 할 수 있게 되어, GPU 활용도를 크게 개선할 수 있다.

GPTQ는 한 번에 $B = 128개$의 column에 알고리즘을 적용하며, updates를 해당 column들과 $\bold{H}^(-1)$의 해당 $B \times B$ 블록으로 제한한다.
Block이 완전히 처리된 후에, 아래에 제시된 Euqation (2)와 (3)의 multi-weight version을 사용해 전체 $\bold{H}^(-1)$와 $\bold{W}$ 행렬에 대해 global updates를 수행한다.

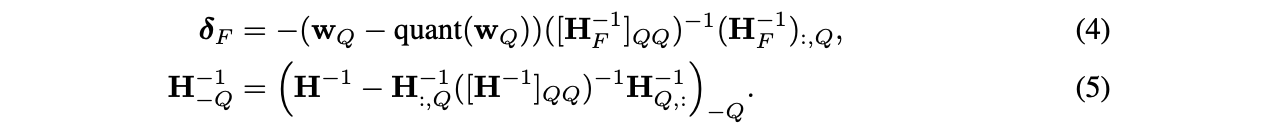
$Q$: set of indices, $\bold{H}^{-1}_{-Q}$: inverse matrix with the corresponding rows and columns removed

---

Step 3: Cholesky Reformulation

핵심: "GPTQ는 Cholesky 분해를 도입하여 수치적(numerical) 안정성 문제를 해결하고, 대규모 모델(large model)에 적용 가능한 알고리즘을 개발했다."

문제

• 수치적 부정확성(numerical inaccuracies)이 large 모델에서 주요 문제가 된다.
  (특히, Step 2의 block updates를 함께 적용하는 경우 더욱더)

• 구체적으로, $\bold{H}^{-1}_F$ 행렬이 indefinite 해질 수 있고, 이로 인해 remaining weights들이 잘못된 방향으로 aggressive하게 update 되어, 해당 layer의 arbitrarily-bad quantization을 초래한다.

• 실전에서, model size가 커질수록 이 문제가 발생할 가능성이 증가한다. 수십억 개 이상의 parameter를 가진 model에선 몇몇 layer에서 이 문제가 거의 확실히 발생함을 관찰했다.

• 주요 issue는 반복적인 Equation (5)의 적용, 즉 반복적인 batch Hessian inverse update로 인한 것으로 보이며, 특히 matrix inversion을 통해 numerical error가 축적되는 것으로 보인다.

• 더 작은 모델의 경우, dampening을 적용하는 것, 즉 H의 대각 요소에 작은 상수 λ (우리는 항상 평균 대각 값의 1%를 선택합니다)를 추가하는 것이 수치적 문제를 피하기에 충분해 보인다.
  그러나 더 큰 모델들은 더 robust하고 일반적인 접근 방식을 필요로 한다.

착안

• $q$번째 가중치를 양자화할 때, $\bold{H}^{-1}_{F_q}$ 행렬(아직 quantized 되지 않은 weights set)의 $q$번째 행에서 $q$번째 요소(diagonal)부터 마지막 요소까지만 필요로 한다. 이는 아직 quantized 되지 않은 weight들과의 관계만을 고려하기 때문이다

해결 방안

• Cholesky decomposition(분해) 도입

  • $\bold{H}^{-1}$ 행렬을 Cholesky 분해하여 수치적으로 더 안정적인 형태로 변환한다.
  • $\bold{H}^{-1}$에서 q번째 row와 column을 제거하는 Equation (3)을 사용하는 것과 본질적으로 같다. 단지, Cholesky 분해의 경우 $[\bold{H}_{F_q}^{-1}]_qq$의 제곱근으로 나눠 정규화해주는 것만 추가된다.

• $\bold{H}^{-1}_{F_q}$에서 필요한 q번째 행의 대각선 이후 요소들만 미리 계산 (선택적 계산)

• 최신 Cholesky kernel을 사용하여 계산 속도 향상

• 약간의 dampening ($\bold{H}$의 diagonal 요소에 작은 상수 추가)을 적용하여 추가적인 수치 안정성(numerical stability) 확보

이 접근 방식은 메모리 사용량을 크게 증가시키지 않으면서도 수치적 안정성을 확보하며, 대규모 모델에서도 robust하게 작동한다.

---

Full Algorithm