[핵심][23.06]OWQ

OWQ 논문
OWQ github

"activation outlier에 대응되는 weight column들은 High precision으로 남기고, 나머지 weight column들을 Q"

Problem Definition

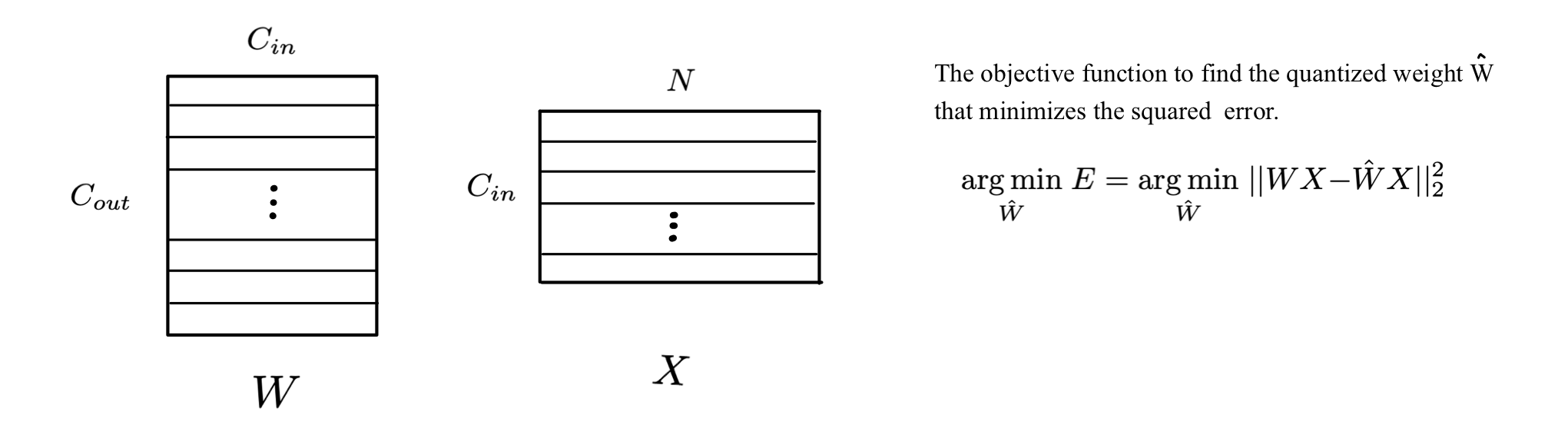
• Given input feature $X \in R^{C_{in} \times N}$, FP weight matrix $W \in R^{C_{out} \times C_{in}}$
  ($C_{in}$: # of input channels, $N$: sequence length of the input, $C_{out}$: # of out channels)

• The objective function to find the quantized weight $\hat{W}$ that minimizes the squared error is defined as follows.
  

---

Motivation

• Core Motivation: activation outlier와 연결되는 weight들은 Q에 더 sensitive하다.

• Row_wise decomposition & Approximation using Taylor Expansion
  전체 error는 각 output channel(row)의 individual error로 나눌 수 있다.

  $\underset{\hat{W}}{\text{argmin}}\ E = \underset{\hat{W}}{\text{argmin}}\|\bold{WX}-\bold{\hat{W}X}\|^2_2$
  $\|\bold{WX}-\bold{\hat{W}X}\|^2_2 = \sum^{C_{out}}_{i=1}\|\bold{W}_{i,:}\bold{X} - \bold{\hat{W}}_{i,:}\bold{X}\|$

  이렇게 전체 error를 각 output channel(row)의 individual error로 나누게 되면, 두 가지 중요한 양상을 얻을 수 있다.
  $\\$
  1. output channel 간의 Hessian interaction이 없다.(OBC, GPTQ)
  구체적으로, layer-wise quantization error에 관한 Hessian은 다음과 같다.
  
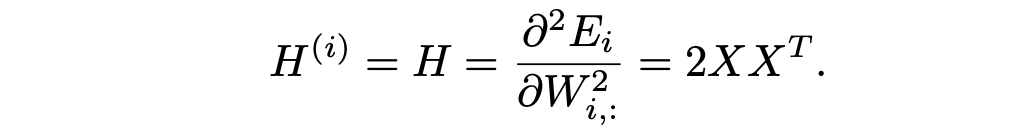
  2. individual error term은 Taylor expansion을 사용해 approximation될 수 있다.(AdaRound)

  $\Delta \bold{W}_{i,:} = \bold{W}_{i,:} - \bold{\hat{W}}_{i,:}$

  일때, $i$-th output channel의 error는 다음과 같이 표현할 수 있다.

  $\bold{E}_i = \|\bold{W}_{i,:}\bold{X} - \bold{\hat{W}}_{i,:}\bold{X}\ \|^2_2 \approx \Delta\bold{W}_{i,:} \ \bold{H} \ \Delta\bold{W}_{i,:}^T$

  equation을 통해 layer-wise quantization 관점에서, output error는 Hessian과 magnitude of weight purturbation에 direct하게 연관돼있다.

• LLM.int8(), SmoothQuan는 LLM activation의 특정 feature dimension들이 다른 값에 비해 매우 큰 outlier를 가짐을 보고했다.

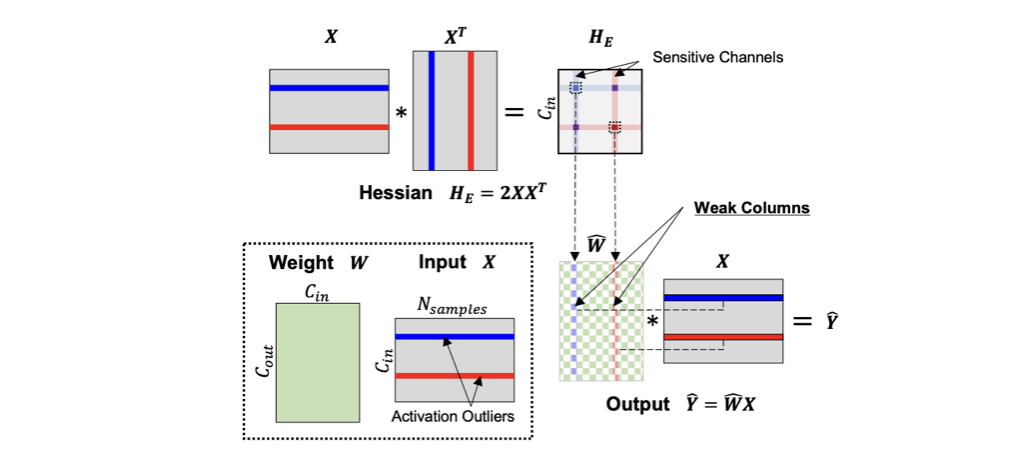
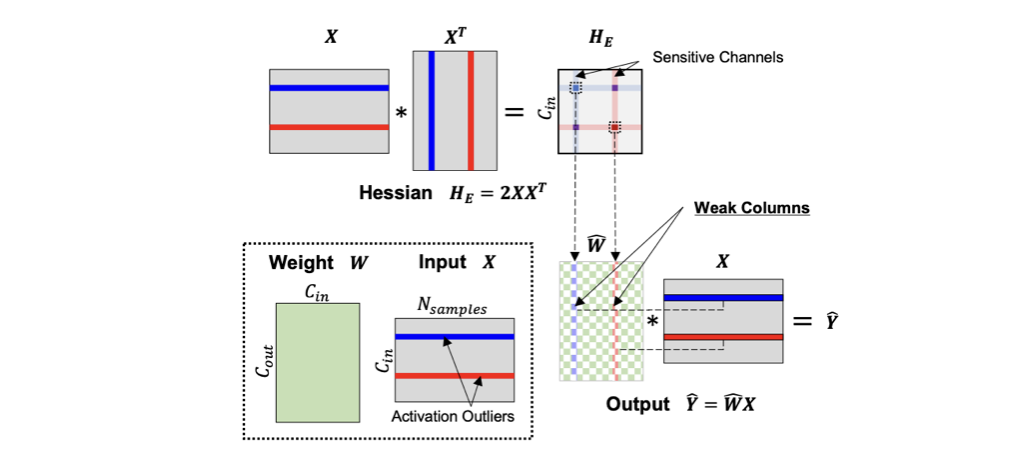
  • 아래 Figure와 같이, activation outliers는 $H$의 몇몇 elements들이 비이상적으로 큰 값(exceptionally high values)을 갖도록 만든다.
    

  • 이러한 Hessian value의 비정상적인 증가는, 이에 대응되는 weight channels의 Q sensitivity를 증가시킨다.

  • 아래 수식에서도 볼 수 있듯, 같은 정도의 weight purturbation이 존재할 때, $H$의 큰 값으로 인해 error $\bold{E} _i$가 크게 변할 수 있다.

    $\bold{E}_i = \|\bold{W}_{i,:}\bold{X} - \bold{\hat{W}}_{i,:}\bold{X}\ \|^2_2 \approx \Delta\bold{W}_{i,:} \ \bold{H} \ \Delta\bold{W}_{i,:}^T$

• 본 논문에서는 Q에 sensitive한 weight를 "weak column"으로 지칭한다.
  (= activation outlier와 연관되어 있는 weight in a specific input channel)

• 모든 weight를 동일한 bit-width로 Q를 하면, weak column으로 인한 error가 커질 수 있다.

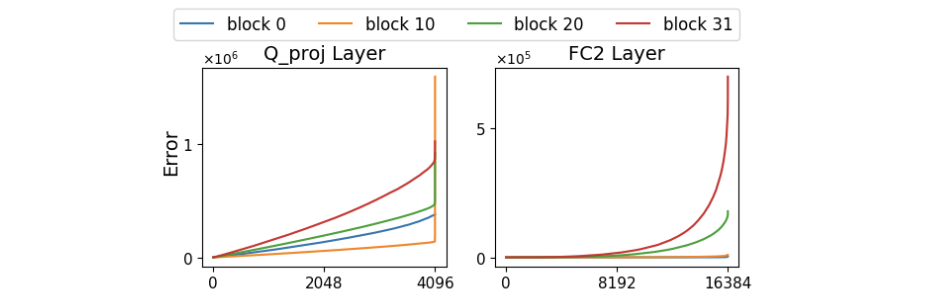
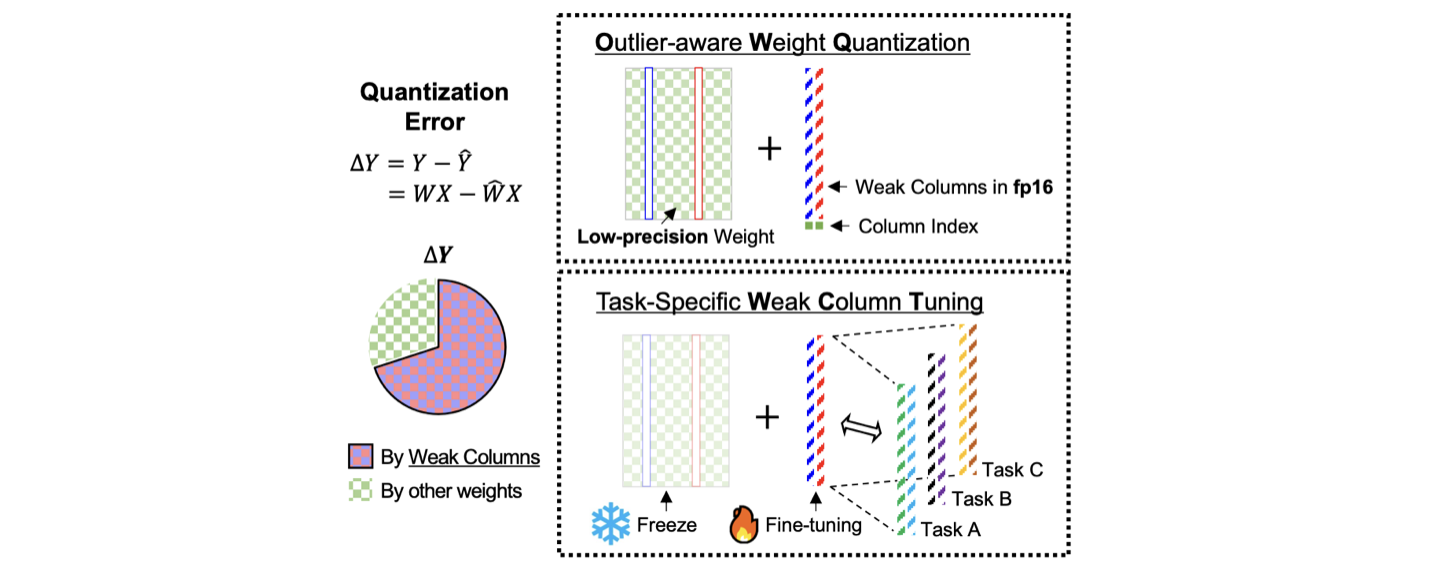
  • Figure 2는 error의 큰 부분이 a limited number of channels(weak columns)로부터 발생함을 보여준다.
  • 따라서, 이 weak column들을 특별히 따로 다루는 방법이 필요하다.
    

• 따라서, $\bold{W}$에서 weak column들을 identify해서, 이들은 Q하지 않고 high precision으로 냅두고,
  나머지 column은 extreme low-precision으로 Q하는 방식을 제안한다.

---

Method

Quantization

sensitivity-aware mixed-precision
quantization에 sensitive한 weight column은 high-precision(FP16)으로 저장하고, 나머지 column은 low-precision으로 Q한다.

---

sensitivity 정의
sensitivity of $j$-th weight column

where $\lambda_j$: $j$-th diagonal element of the Hessian matrix

위 metric으로 top-$k$ sensitive columns를 고른다.

---

OPTQ framework

• 어떠한 low-precision scheme도 사용 가능하지만, OPTQ 역시 sequential column-wise Q를 활용하므로, OPTQ를 선택했다.

• 또 하나 주목할 점은, weak column을 OPTQ의 가장 마지막 순서로 배치하면, 다른 column들에서 발생한 Q error를 high-precision인 weak column이 크게 compensation할 수 있다.

• Quantization Configuration Search

  • OPTQ의 경우 min-max Q를 사용하지만, 우리는 truncation을 사용했다.
    Learned Step Size Q, BRECQ, Loss-Aware PTQ 연구에서 truncation이 Q error를 크게 줄일 수 있음을 보였기 때문이다.

  • Q configuration인 step size와 Q range는 간단한 2D grid search를 사용해 정했다.
    truncation과 함께 rounding-to-nearest를 사용해 Q error를 줄이는 최적의 parameter를 찾았고, 이 값을 토대로 OPTQ를 적용했다.

---

Fine-Tuning

• based model을 OWQ로 quantize한 이후, high-precision인 "weak columns만" fine-tuning한다.
• high-precision columns은 조금의 변화도 output에 큰 영향을 미친다.
  

---

Results

3.1-bit OWQ는 4-bit OPTQ 모델과 유사한 성능을 보임.

---

Novelty

extremely low-precision weight quantization에서 activation outliers의 존재를 고려하고, fine-tuning과 밀접하게 integration한 첫 번째 연구.