1. Introduction

• 카메라는 컴퓨터 비전에서 중요한 도구 중 하나임. 카메라를 어떻게 모델링할 수 있을까?

2. Pinhole cameras

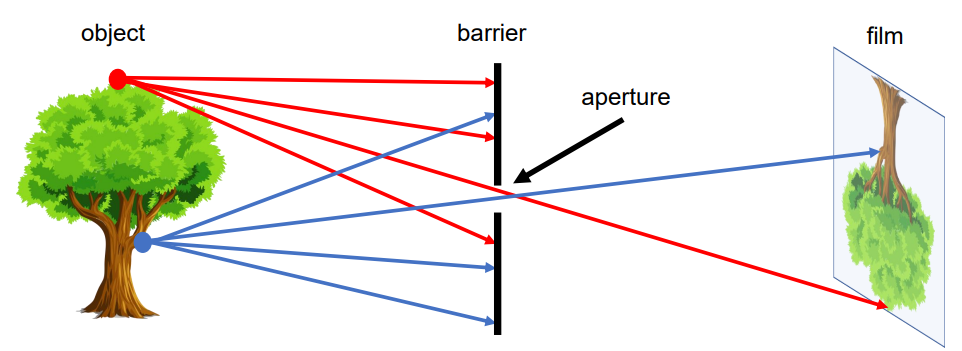
• 핀홀 카메라의 시스템을 설계해보자. 이는 3D 물체와 사진 필름 및 센서 사이에 작은 구멍 (small aperture)이 있는 barrier을 배치함으로써 설계할 수 있음.

  • 3D 물체의 모든 지점에서 여러 개의 Ray가 방출되고, Barrier에 의해 ray 중 소수의 광선만 구멍을 통해 필름에 도달하게 되어 3D 물체의 점과 필름의 점 사이에 일대일 매핑이 가능하게 함.
    
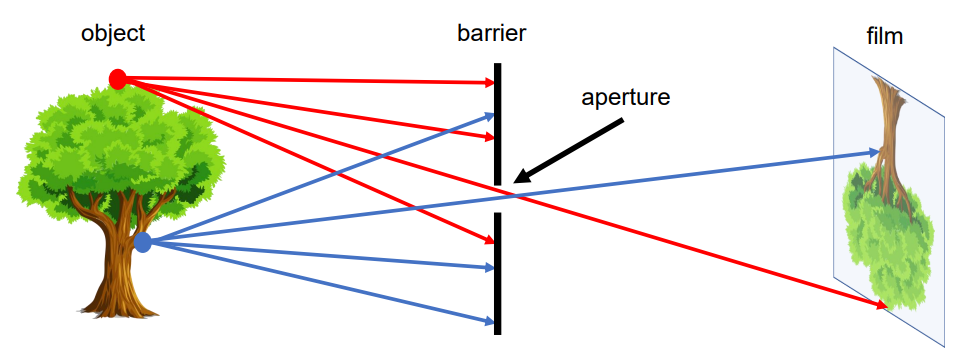
    • 만약 Barrier가 없다면, 필름의 모든 지점은 물체의 모든 지점에서 방출되는 ray에 영향을 받음.
  • 이러한 모델을 핀홀 카메라 모델이라고 함.

• 좀 더 formal한 핀홀 카메라 모델은 다음과 같음.
  

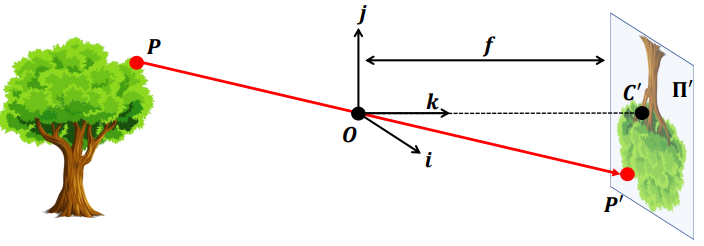
  • 여기서 film은 image 혹은 retinal plane (레티날 평면)이라고 불림.
  • aperture은 pinhole ($O$) 혹은 Center of the camera라고 불림.
  • image와 pinhole ($O$) 사이의 거리는 focal lenght ($f$) 라고 불림.
    • image가 $O$와 3D 물체 사이에 존재한다고 가정하면 이러한 가상 image는 virtual image 또는 virtual retinal plane라고 함.
      • 이러한 virtual image는 image의 투영 물체와 동일하며 단지 scale (similarity) 변화만 있음.

• 이러한 핀홀 카메라를 어떻게 사용할까?

  • 실제 3D 물체의 한 지점 $P = [x\space y \space z]^T$라고 하면, 이 $P$는 image의 평면 $Π'$에 매핑되거나 투영되어 $P' = [x'\space y']^T$ 를 만들어 냄. (해당 강의에서 $'$는 투영을 나타냄. )
    
  • $O$ 자체에서도 이미지 평면에 투영되어 $C'$를 만들어 냄.
  • 여기서 $O$를 중심으로 하는 image 평면에 수직인 축 $k$를 정의할 수 있고, 이 $k$와 수직인 $j$와 $i$를 정의하여 camera reference system 또는 camera coordinate system이라고 불리는 좌표계를 정의
    • $C'$와 $O$를 잇는 선을 optical axis라고 부름.

• $P'$와 $P$의 관계를 도출하면 3D 세계가 어떻게 이미지로 찍히는 지 이해할 수 있음.

  • 삼각형 $\vartriangle P'C'O$는 $P$, $O$, $(0, 0, z)$로 구성된 삼각형과 닮음이므로 닮음비를 이용( ($\frac{x’}{x} =\frac{f}{z} ,\frac{y’}{y} =\frac{f}{z}$ )하면

    $P' = [x' \space y']^T = [f\frac{x}{z} \space f\frac{y}{z}]^T -----(1)$

  

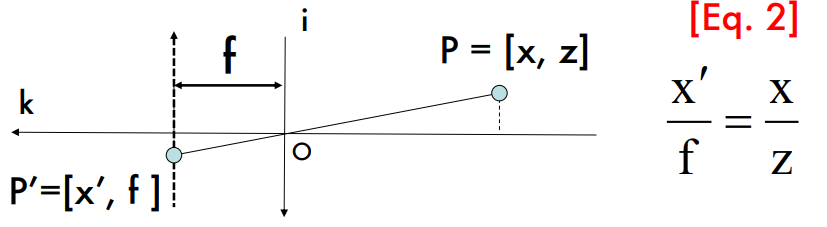
• 이 핀홀 모델에서 우리는 aperture가 Single point로 가정하지만, 실제 이 aperture를 무한히 작다고 가정할 수 없음.

  • aperture에 크기에 따른 이미지의 변화
    
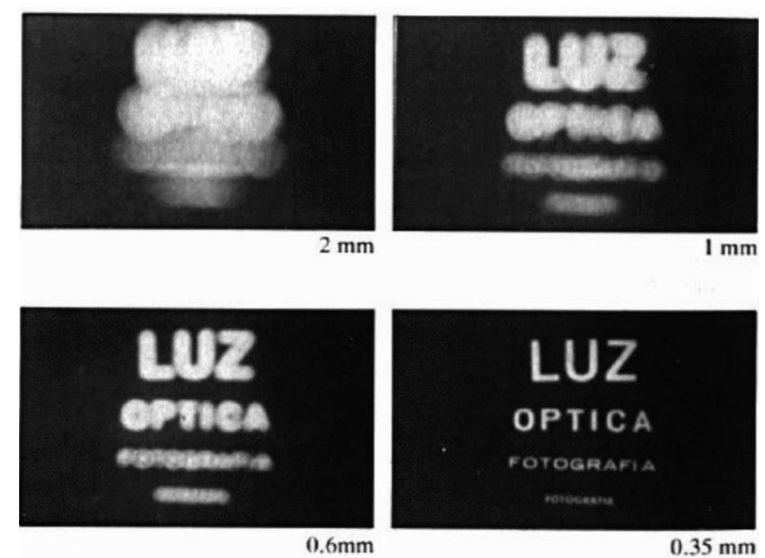
    • aperture 크기가 커짐에 따라 barrier을 통과하는 ray의 수가 증가하게 되어 image의 각 지점은 여러 ray에 영향을 받아 이미지가 흐려짐
    • 반면, aperture 크기가 작아짐에 따라 ray 수가 감소하여 이미지가 선명해지지만 어두워짐.
  • 그렇다면, 선명하고 밝은 이미지를 촬영할 수 있는 카메라를 발명할 수 있을까?

3. Cameras and lenses

• 현재 우리가 사용하고 있는 대부분의 카메라들은 이러한 선명도와 밝음의 trade-off를 렌즈를 통해 빛을 분산시키거나 집중시켜 이를 완화함.
• 즉, 핀홀을 렌즈로 대체하면 $P$에서 나오는 모든 ray들이 렌즈에 의해 굴절되어 이미지 평면의 한 점 $P'$에 수렴함.
  • 이를 통해 빛의 광선이 차단되는 문제가 제거됨.
    
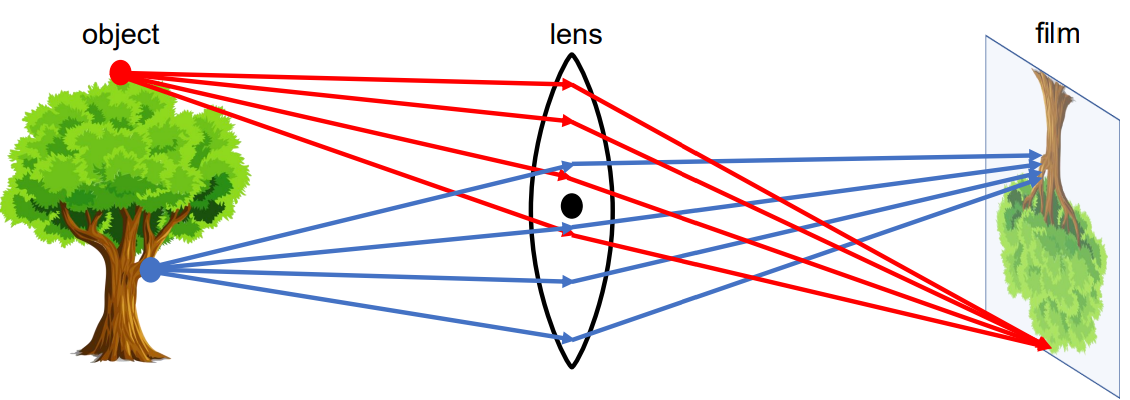
  • 하지만 이러한 특성은 모든 3D 점에 대해 성립하지 않고, 특정 점에서만 성립함.
    • 파랑 점의 ray들은 한 점으로 수렴되지 않음. 즉, 물체가 초점에 맞는 특정 거리가 있음.
    • 이는 computer graphics분야의 depth of field(DOF)라는 개념과 관련이 있음.
• 렌즈의 다른 특성은 렌즈의 optical axis과 평행하게 이동하는 ray들은 focal point라는 점에 수렴함.
  
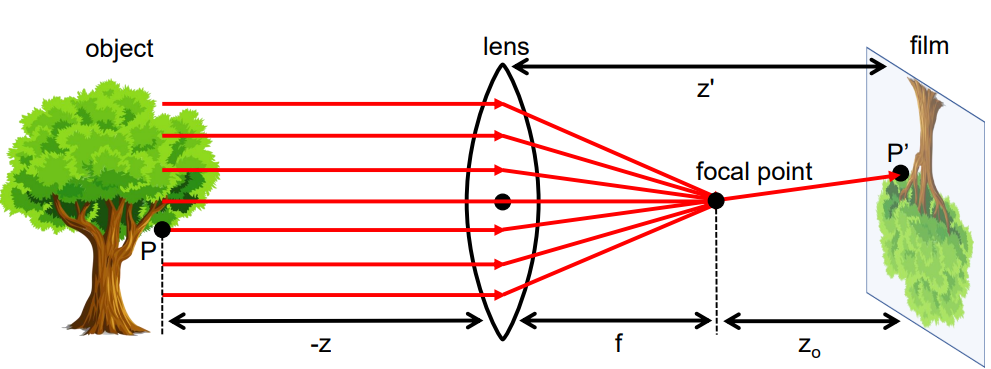
  • focal point와 렌즈 중심 사이의 거리는 focal length $f$임.
  • 핀홀 모델과 유사하게 렌즈에서도 $P$와 $P'$ 간의 관계를 나타낼 수 있음.
    $P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} z'\frac{x}{z} \\ z'\frac{y}{z} \end{pmatrix}$
  • 핀홀 모델에서는 $z' = f$였지만, 렌즈 모델에서는 $z' = f + z_0$임에 주의
• 이러한 유도 과정은 paraxial (optical axis과 가까운 ray) 혹은 thin lens을 가정하므로 paraxial refraction model라고 함.
  • 근축 가정(paraxial assumption) = $\sin(\theta)$을 $\theta$로 대체
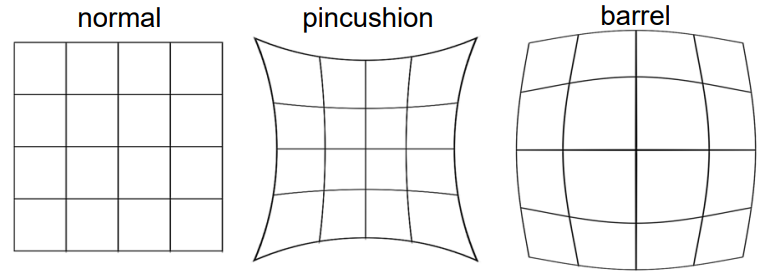
  • 이는 optical axis에서의 거리에 따라 image의 magnification가 변하는 현상인 방사 왜곡(radial distortion)과 같은 수차(aberration)를 유발함.
    • magnification가 증가하면 pincushion distortion (핀쿠션 왜곡)이라 함.
    • magnification가 감소할 때는 barrel distortion(배럴 왜곡)이라고 함. (보통 fish-eye lenses을 사용할 때 발생)
      

4. Going to digital image space

• 3D 공간을 digital image로 모델링할 때 고려해야 할 사항을 알아보자. 해당 섹션의 모든 결과는 핀홀 모델을 사용하지만, paraxial refraction model에도 적용이 가능함.
• 3D 공간에서의 점 $P$는 2D 점 $P'$로 $R^3 → R^2$ 매핑되는데 이를 projective transformation(투영 변환)이라고 함.
• 하지만 다음과 같은 이유로 3D 물체가 image 평면으로 투영된 것이 실제 디지털 이미지에서 우리가 보는 것과 같지 않음.
  • digital image의 점들은 image 평면의 점들과 다른 reference system을 가짐.
  • digital image는 이산적인 픽셀이지만, image 평면의 점들은 연속적임.
  • 실제 센서들은 non-linearity (왜곡)을 가질 수 있음.
• 따라서 이를 해결할 수 있는 몇 가지 transformation을 알아보자.

4-1. The Camera Matrix Model and Homogeneous Coordinates

4.1.1 Introduction to the Camera Matrix Model

• Camera matrix model (카메라 행렬 모델)은 3D 물체의 점 $P$가 이미지 좌표 $P'$에 맵핑되는 몇 가지 파라미터로 표현됨.
  1. $c_x$, $c_y$ = image 평면과 digital image 좌표가 어떻게 변환에 의해 달라질 수 있는지를 설명함.
     • image 평면 좌표는 $k$축이 image 평면과 교차하는 지점에 원점 $C'$를 갖음.
     • 하지만, digital image 좌표는 일반적으로 이미지의 최하단 모서리에 원점을 가짐.
     • 따라서 image와 digital image의 맵핑을 위해 $c_x$, $c_y$ 평행 이동을 이용함.
       $P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} f\frac{x}{z} + c_x \\ f\frac{y}{z}+c_y \end{pmatrix}$
  2. $k$, $l$ = digital image의 점들이 픽셀로 표현되는 것과 image 평면의 점이 측정 단위 (cm)로 표현되는 것을 보정
     • 이 파라미터들은 픽셀/cm 등의 단위를 가짐.
     • 픽셀의 가로세로 비율이 항상 1:1이 아니기에, $k$와 $l$는 다를 수 있음. $(k = i$이면 정사각형 픽셀)
       $P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} fk\frac{x}{z} + c_x \\ fl\frac{y}{z}+c_y \end{pmatrix} = \begin{pmatrix} \alpha\frac{x}{z} + c_x \\ \beta\frac{y}{z}+c_y \end{pmatrix}$
• 이러한 투영이 선형변환이라면, 위 식을 행렬과 벡터로 나타낼 수 있지만, 선형 변환이 아님 ($z$를 나누므로).
  • 하지만, 행렬-벡터 곱으로 표현하는 것이 유용하므로 비선형성을 고려하더라도 행렬-벡터 곱으로 나타내길 원함.
  • 이러한 해결책이 Homogeneous Coordinates

4.1.2. Homogeneous Coordinates

• 새로운 좌표를 추가하여 $P' = (x', y')$를 $(x', y', 1)$로 변환하자. ($P = (x, y, z)$도 $(x, y, z, 1)$로 변환)
  • 이러한 확장된 공간을 homogeneous coordinate system이라고 함.
  • 벡터와 homogeneous coordinate 간의 equality(동일성)은 마지막 좌표가 1일 때만 성립함.
  • 마지막 좌표가 1이 아니라면, homogeneous coordinate ($v_1, ..., v_n, w$)에서 유클리드 좌표 ($\frac{v_1}{w}, ..., \frac{v_n}{w}$)를 얻음.
• 위 식을 homogeneous coordinate을 사용해서 나타내면
  $P'_h=\begin{bmatrix} \alpha x+ c_xz \\ \beta y+ c_yz \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y &0 \\ 0 & 0 & 1 &0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y &0 \\ 0 & 0 & 1 &0 \\ \end{bmatrix} P_h$

  • 앞으로 별도의 언급이 없는 한 homogeneous coordinate을 사용할 것이고, 이에 따라 h 인덱스를 사용하지 않을 것임.

    $P'=\begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y &0 \\ 0 & 0 & 1 &0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y &0 \\ 0 & 0 & 1 &0 \\ \end{bmatrix} P = MP$

  • 이를 더 세분화하면

    $P'= MP = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y &0 \\ 0 & 0 & 1 &0 \\ \end{bmatrix} \begin{bmatrix} I & 0 \end{bmatrix} P = K \begin{bmatrix} I & 0 \end{bmatrix} P ----- (7)$
    • K 행렬을 camera matrix라고 부름

4.1.3. The Complete Camera Matrix Model

• 위에서 정의한 camera matrix $K$는 카메라의 특성과 모델을 설명하는 $c_x, c_y, k, l$ 파라미터가 포함됨.
  • 하지만 이 공식에서는 skewness(비대칭도)와 distortion(왜곡)을 해결할 수 있는 파라미터가 없음.
• skewness(비대칭도)
  

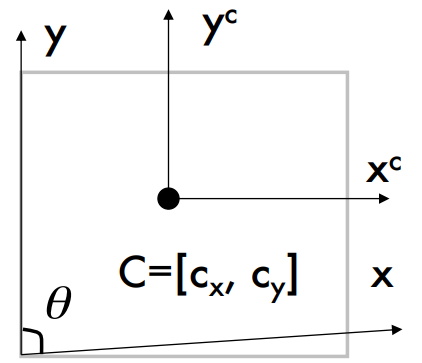
  • 이는 두 축 사이의 각도가 90도 보다 크거나 작은 상태를 의미함. 보통 센서의 불량으로 인해 발생함.

  • skewness를 고려한 $K$

    $K = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & -\alpha cot(\theta) & c_x \\ 0 & \frac{\beta}{sin\theta} & c_y\\ 0 & 0 & 1 \end{bmatrix}$
• distortion(왜곡)
  • 이 수업에서는 distortion를 무시
• 따라서 이 수업의 camera matrix은 5개의 자유도를 가짐.
  • focal length로 인한 자유도 2개 ($\alpha, \beta$), offset으로 인한 자유도 2개 ($c_x$, $c_y$), skewness로 인한 자유도 1개 ($\theta$)
  • 이러한 파라미터들은 카메라에 내재된 고유한 파라미터이므로 intrinsic parameters (내재적 파라미터)라고 함.

4.2 Extrinsic Parameters

• 지금까지 카메라의 intrinsic parameters를 통해 $P$와 $P'$ 사이의 매핑을 알아봤다. 하지만 다른 좌표계에서 3D world에 대한 정보가 주어지면 어떻게 할까?

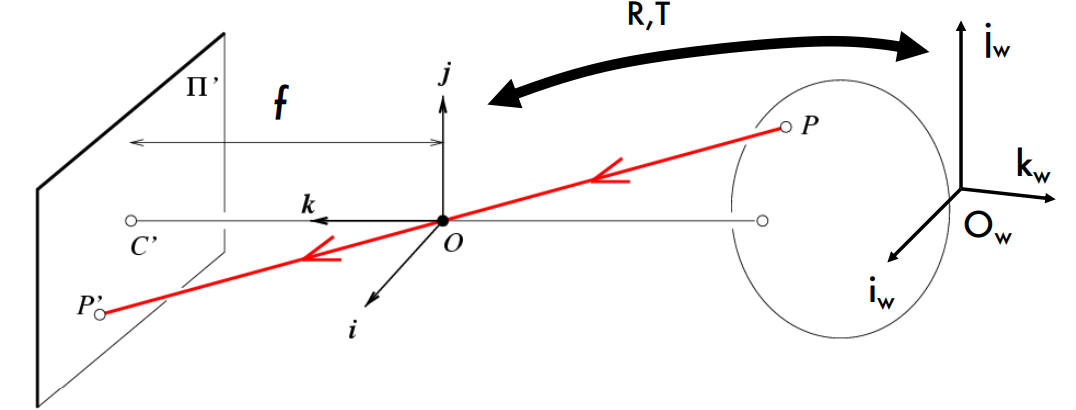
  • 회전 행렬 $R$과 변환 벡터 $T$로 표현되는 추가적인 변환이 필요함. 즉, camera coordinates과 다른 coordinates 사이의 매핑이 필요함.
    

• 만약 다른 좌표계의 3D 물체의 한 점 $P_w$이 주어지면, 그 점의 camera coordinates은

  $P = \begin{bmatrix} R & T \\ 0 & 1 \\ \end{bmatrix} P_w$

  로 표현됨.
  

• 이를 방정식 (7)에 대입하고 단순화하면 다음과 같음.

  $P' = KP = K\begin{bmatrix} R & T \\ \end{bmatrix} P_w = MP_w$

  

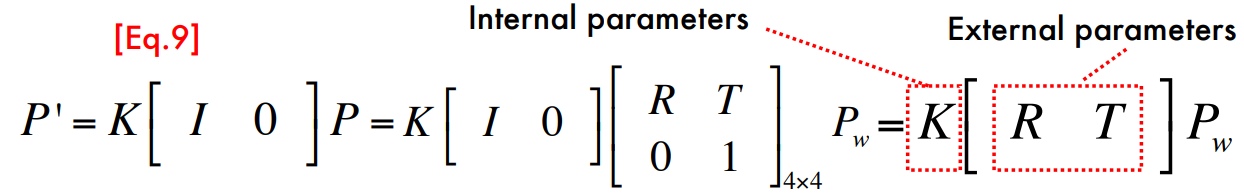
  • 이 R과 T 파라미터는 카메라 외부의 파라미터이므로 extrinsic parameters(외재적 파라미터) 라고 함.

  • full projection matrix $M$은 extrinsic parameters와 intrinsic parameters로 구성되어 있으며 (3, 4) 크기와 11개의 자유도를 가짐.

    • 왜 (3, 4) 크기와 11의 자유도를 가질까?
      

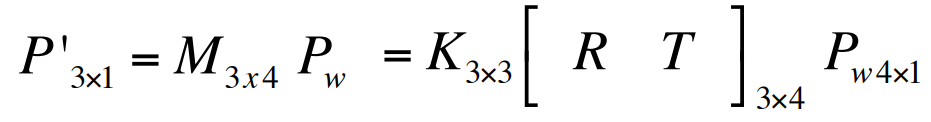
      • 회전 행렬 R은 (3, 3)의 행렬이며, 3개의 자유도를 가지고 있음. (회전각도 $\alpha$, $\beta$, $\gamma$ 3개)
        $R = R_x(\alpha)R_y(\beta)R_z(\gamma) \\ (R_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \end{bmatrix}, R_y = \begin{bmatrix} cos(\beta) & 0 & sin(\beta) \\ 0 & 1 & 0 \\ -sin(\beta) & 0 & cos(\beta) \end{bmatrix}, R_z = \begin{bmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0 \\ 0 & 0 & 1 \end{bmatrix}$
      • 변환 벡터 T는 (3,1) 벡터로, 위치를 나타내는 3개의 자유도를 가짐.
        $T = \begin{bmatrix} T_x \\ T_y \\ T_z \end{bmatrix}$