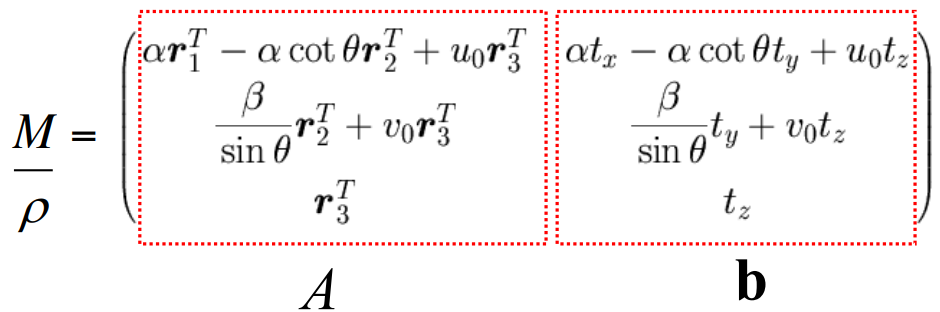5. Camera Calibration

• 앞 강의를 통해 우리는 3D world에서 digital image로 변환을 위해서는 카메라의 intrinsic, extrinsic parameter을 알아야 함을 배웠다.

• 하지만 파라미터를 알 수 없는 임의의 카메라로 찍은 이미지에서 이러한 파라미터를 유추할 수 있는 방법이 있을까?

  • camera calibration이 바로 파라미터를 추정하는 방법임.

• Camera Calibration을 위해 체커보드와 같은 calibration rig를 사용하며 원점 $O_w$와 축 i$_w, j_w, k_w$를 가짐.

  

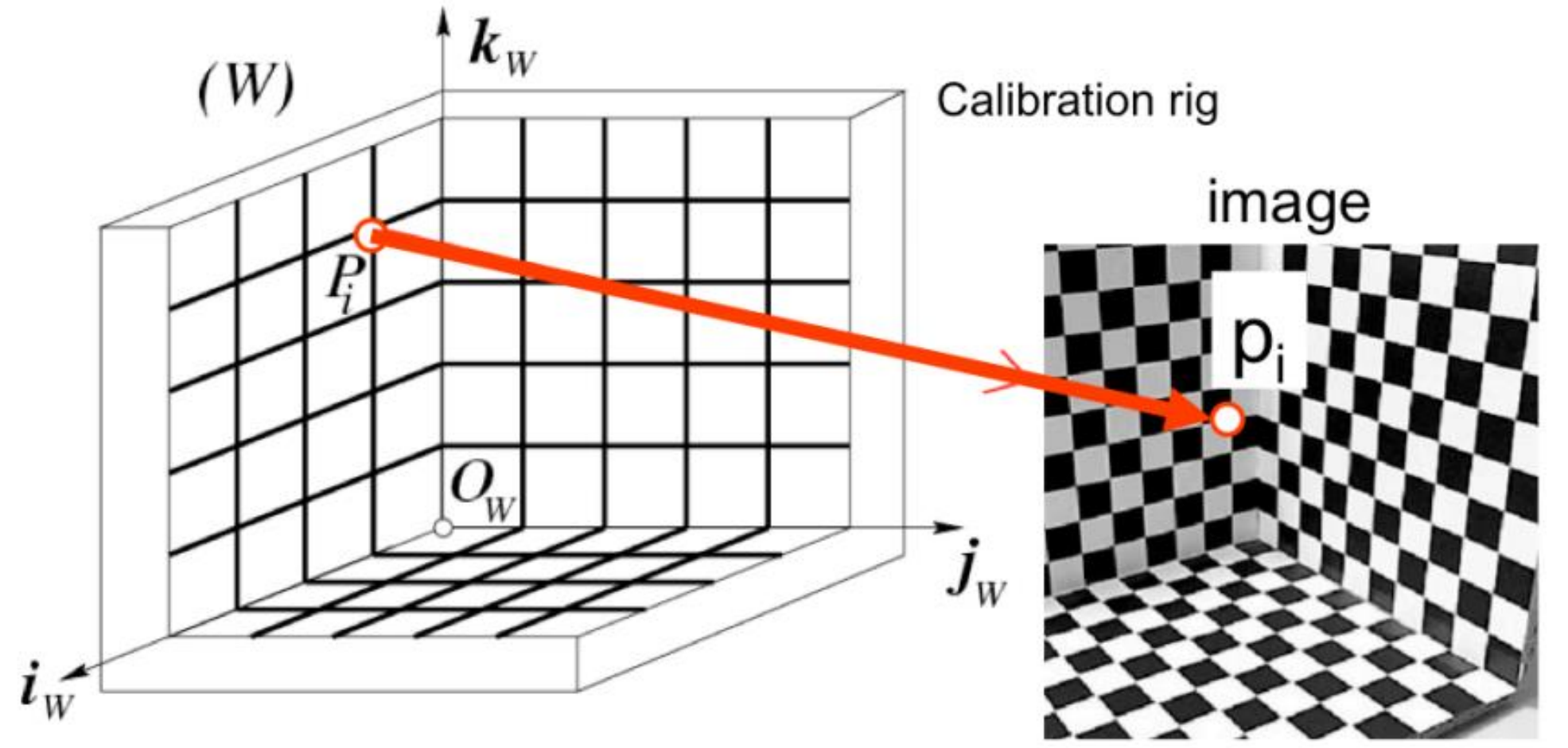
  • 실제 세계의 rig에 점 $P_1, …. P_n$의 정보를 알고 있으므로 image에서 이에 해당하는 점 $p_1, …p_n$을 얻을 수 있음.

• 이러한 n개의 $P_i$, $p_i$의 대응 관계가 있을 때, 각 행 $m_1, m_2, m_3$를 가지는 Camera Matrix $M$와의 선형 방정식을 만들 수 있음.

  $p_i = \begin{bmatrix} u_i\\ v_i \end{bmatrix} = MP_i = \begin{bmatrix} \frac{m_1P_i}{m_3P_i}\\ \frac{m_2P_i}{m_3P_i} \end{bmatrix}$
  • 식 풀이
    $M = \begin{bmatrix} m_1\\ m_2\\ m_3 \end{bmatrix}일 \space 때, MP_i = \begin{bmatrix} m_1 P_i\\ m_2 P_i\\ m_3 P_i \end{bmatrix}$
    이고, 벡터와 homogeneous coordinate 간의 equality(동일성)은 마지막 좌표가 1일 때만 성립하므로 $m_3P_i$를 각 벡터에 나누면
    $MP_i = \begin{bmatrix} \frac{m_1P_i}{m_3P_i}\\\\ \frac{m_2P_i}{m_3P_i} \end{bmatrix}$
  • 각 $P_i$, $p_i$는 두 개의 방정식을 제공하며, 이를 통해 m을 풀기 위한 두 가지 constraints(제약 조건)을 제공함.

• 따라서 앞에서 배웠던 것처럼 Camera Matrix에 11가지의 파라미터가 필요하므로 최소한 6개의 대응 관계를 알아야 함.

  • 하지만, 노이즈 등으로 인해 실제로는 더 많은 대응 관계가 필요하며, n개의 대응 관계가 주어지면 전체 선형 방정식은 다음과 같음.

    $u_1(m_3P_1) - m_1P_i = 0 \\ v_1(m_3P_1) - m_2P_i = 0 \\ .\\ .\\ .\\ u_n(m_3P_1) - m_1P_i = 0 \\ v_n(m_3P_1) - m_2P_i = 0 \\$

• 이를 행렬-벡터 곱으로 표현하면

  $\begin{bmatrix} P^T & 0^T & -u_1P_1^T \\ 0^T & P_1^T & -v_1P_1^T \\ & . \\ & . \\ & . \\ P_n^T & 0^T & -u_nP_1^T \\ 0^T & P_n^T & -u_nP_1^T \\ \end{bmatrix} \begin{bmatrix} m_1^T \\ m_2^T \\ m_3^T \end{bmatrix} = \bold{P}m = 0$

• 하지만, $2n > 11$일 때, trivial solution(자명한 해)는 $m_1 = m_2 = m_3 = 0$ 임. (homongeneous linear system이므로)

• 비자명한 해(nonzero solution = nontrivial solution)가 있다고 가정하면, 행렬 $P$의 열들이 선형종속일 때이므로 비자명한 해 $m$에 $∀k \in \R$ 즉, 모든 실수 $k$를 곱해도 비자명한 해에 속함.

  • 따라서 해를 제한하기 위해 다음과 같은 최소화를 수행함.
    $\underset{m}{\text{minimize}} \space ||\bold Pm||^2 subject \space to \space ||m||^2 = 1$
  • 위 식을 풀기 위해 SVD (특이값 분해)를 사용함. $P = UDV^T$일 때, |$|\bold Pm||^2$을 최소화하기 위한 m은 m = V의 마지막 열(벡터)임.
    • 증명 (Section 5.3 of Hartley & Zisserman on pages 592-593)
      

• 이 벡터 m을 행렬 M으로 재구성하면, 이 M은 실제 카메라 행렬의 스칼라 배수임.

  $ρM = \begin{bmatrix} \alpha r_1^T - \alpha cot(\theta) r_2^T+c_xr_3^T & \alpha t_x - \alpha cot(\theta) t_y+c_xt_z \\\\ \frac{\beta}{sin\theta}r_2^T+c_yr_3^T & \frac{\beta}{sin\theta}t_y+c_yt_z \\\\ r_3^T & t_z \end{bmatrix}$
  • 식 유도
    • 우리는 이전 시간에 Full projection matrix M이 $K[R\space\space T]$라는 것을 배웠다.
    • 여기서
      $K =\begin{bmatrix} \alpha & -\alpha cot(\theta) & c_x \\ 0 & \frac{\beta}{sin\theta} & c_y\\ 0 & 0 & 1 \end{bmatrix}, R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \begin{bmatrix} r_1 \\ r_2 \\ r_3 \end{bmatrix}, T = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}$
      라고 할 때, $[R \space \space T]$는 다음과 같으므로
      $[R \space \space T] = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \begin{bmatrix} --r_1-- & t_x\\ --r_2-- & t_y\\ --r_3-- & t_z\\ \end{bmatrix}$
      $M = K[R\space\space T]$은 다음과 같음.
      $M = K[R\space\space T]= \begin{bmatrix} \alpha & -\alpha cot(\theta) & c_x \\ 0 & \frac{\beta}{sin\theta} & c_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} --r_1-- & t_x\\ --r_2-- & t_y\\ --r_3-- & t_z\\ \end{bmatrix} = \begin{bmatrix} \alpha r_1^T - \alpha cot(\theta) r_2^T+c_xr_3^T & \alpha t_x - \alpha cot(\theta) t_y+c_xt_z \\\\ \frac{\beta}{sin\theta}r_2^T+c_yr_3^T & \frac{\beta}{sin\theta}t_y+c_yt_z \\\\ r_3^T & t_Z \end{bmatrix}$

• 여기서 scaling parameter ρ로 나누면

  $M = \frac{1}{ρ}\begin{bmatrix} \alpha r_1^T - \alpha cot(\theta) r_2^T+c_xr_3^T & \alpha t_x - \alpha cot(\theta) t_y+c_xt_z \\\\ \frac{\beta}{sin\theta}r_2^T+c_yr_3^T & \frac{\beta}{sin\theta}t_y+c_yt_z \\\\ r_3^T & t_Z \end{bmatrix} = \begin{bmatrix} A & b \end{bmatrix} = \begin{bmatrix} a_1^T \\ a_2^T \\ a_3^T \\ \end{bmatrix}\begin{bmatrix} b_1 \\ b_2\\ b_3 \\ \end{bmatrix}$

  

  • 이를 통해 intrinsic parameter는

    $ρ = \pm \frac{1}{\|a_3\|} \\ c_x=\rho^2(a_1 \cdot a_3) \\ c_y= \rho^2(a_2 \cdot a_3) \\ θ=cos^{−1}(-\frac{(a_1×a_3) ⋅(a_2×a_3)}{∥a_1×a_3∥⋅ ||a_2×a_3||}) \\ α=ρ2∥a_1×a_3∥sinθ \\ β=ρ2∥a_2×a_3∥sinθ$

    이고, extrinsic parameter는

    $r_1= \frac{a_2 \times a_3}{\|a_2 \times a_3\|} \\ r_2=r_3×r_1 \\ r_3=ρa_3 \\ T=ρK^{−1}b$

    이다. (Forsyth & Ponce textbook 138p)

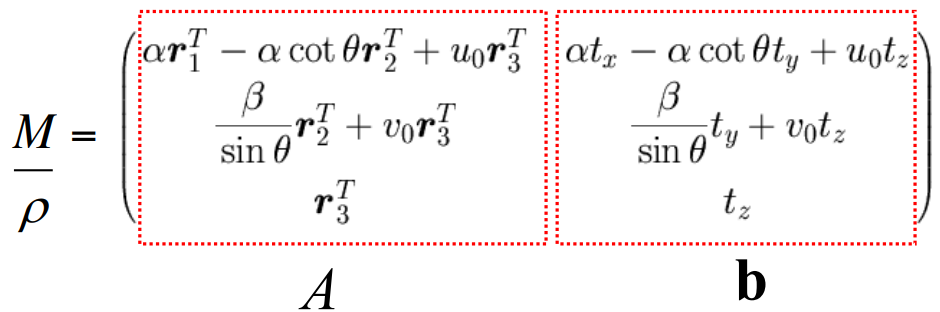
• 여기서 주의해아 할 점은 degenerate 경우 즉, $P_i$들이 같은 plane에 있는 경우, 이 시스템을 풀 수 없음. 이러한 점들을 degenerate configurations라고 함.

6. Handling Distortion in Camera Calibration

• 지금까지 Distortion이 없는 이상적인 렌즈를 다뤄왔지만, 실제 렌즈는 rectilinear
  projection (직선 투영)을 할 수 없는 경우가 있음
  
• 렌즈는 symmetric하므로 Distortion 역시, symmetric함.
• 따라서 isotropic transformation을 통해 distortion을 모델링 해보면, (즉, 각 점이 동일한 비율로 스케일링된다고 가정하여 모델링 해보면)
  $QP_i = \begin{bmatrix} \frac{1}{λ} & 0 & 0 \\ 0 & \frac{1}{λ} & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} MP_i = \begin{bmatrix} u_i \\ v_i \end{bmatrix} = p_i$
  이고, $\begin{bmatrix} \frac{1}{λ} & 0 & 0 \\ 0 & \frac{1}{λ} & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} M = Q = \begin{bmatrix} q_1 \\ q_2 \\ q_3 \end{bmatrix}$이므로 $QP_i = \begin{bmatrix} \frac{q_1P_i}{q_3P_i} \\\\ \frac{q_2P_i}{q_3P_I} \end{bmatrix}$ 이고,
  $u_iq_3P_i = q_1P_i \\ v_iq_3P_i = q_2P_i$
  이다.
  
• 하지만, 이 시스템은 선형적이지 않으므로 non-linear optimization이 필요함.
• 우리가 다루는 Radial Distortion은 두 좌표 $u_i$와 $v_i$ 사이의 비율은 영향을 받지 않으므로 $\frac{u_i}{v_i}$를 이용하자 . (Radial Distortion가 렌즈 중심에서 얼마나 멀리 떨어지냐에 따라 Distortion이 달라지니까 $\frac{x}{y}$비율만 같으면 $z$축 distortion은 어떤 방향이든 같다는 뜻인 듯..?)
  $\frac{u_i}{v_i} = \frac{\frac{m_1P_i}{m_3P_i}}{\frac{m_2P_i}{m_3P_i}} = \frac{m_1P_i}{m_2P_i}$
• 따라서 n개의 대응관계가 주어졌다고 가정하면,
  $v_1(m_1P_1)−u_1(m_2P_1)=0, ...,v_n(m_1P_n)−u_n(m_2P_n)=0$
  의 시스템을 설정할 수 있음.
  
• 이를 행렬-벡터 곱으로 나타내면
  $L_n = \begin{bmatrix} v_1P_1^T && -u_1P_1^T\\ . && .\\ . && .\\ . && .\\ v_nP_n^T && -u_nP_n^T \end{bmatrix}\begin{bmatrix} m_1^T \\\\ m_2^T \end{bmatrix}$
  이고, 이를 SVD를 통해 $m_1$, $m_2$를 추정하면, $m_3$은
  $p_i =\begin{bmatrix} u_i\\\\ v_i \end{bmatrix} = \frac{1}{λ}\begin{bmatrix} \frac{m_1P_i}{m_3P_i}\\\\ \frac{m_2P_i}{m_3P_i} \end{bmatrix}$
  로 추정 가능함. (image의 점 $p_i$에서 $m_3$를 추정 )