1. Introduction

• 지금까지 camera calibration 또는 single view metrology를 통해 하나의 이미지로부터 intrinsic and extrinsic parameters를 계산하고 3D 세계에 대한 속성을 도출했다.
• 하지만, 일반적으로 단 한 장의 이미지로부터 3D 세계의 전체 구조를 복원하는 것은 3D에서 2D로의 매핑 과정에서 발생하는 intrinsic ambiguity(모호성)때문에 불가능함.
• 위 사진은 남자가 피사의 사탑을 받치고 있는 것으로 보이나 사실 이건 다른 깊이가 이미지 평면에 투영되면서 발생한 착시임.
• 이 섹션에서는 여러 대의 카메라에서의 여러 view point가 얼마나 유용하고, 주변 세계를 더 잘 이해하는 데 어떻게 도움이 되는 지 알아볼 것임.

2. Epipolar Geometry

• multiple view geometry에서 여러 카메라. 3D point, 각 카메라 이미지 평면의 투영 등을 연결하는 기하학을 Epipolar Geometry(에피폴라 기하학) 이라고 부름
  
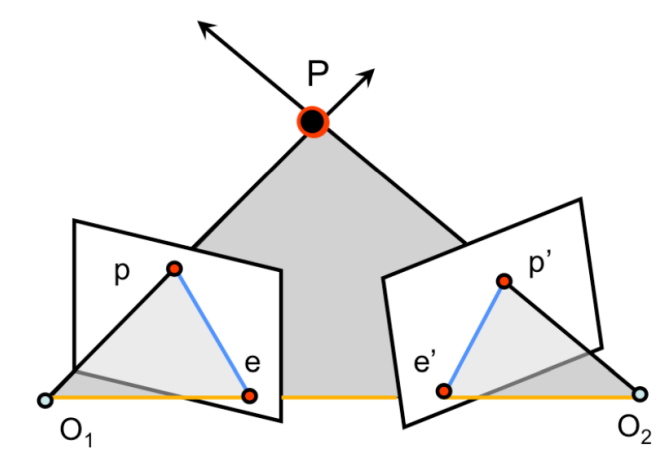
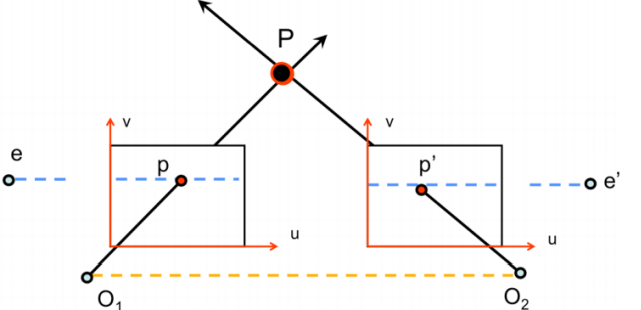
  • 위 사진처럼 표준 에피폴라 기하학은 두 개의 카메라가 동일한 3D 점을 P를 관찰하고, P는 이미지의 $p$, $p'$에 투영됨.
  • 카메라 중심은 $O_1$, $O_2$에 위치하고, 이 둘 사이의 선 (주황색 선)을 baseline이라고 함.
  • 두 카메라 중심 $O_1$, $O_2$과 P로 정의된 평면 (회색 평면)을 에피폴라 plane이라고 함.
  • baseline과 각 이미지 평면의 교점을 epipoles $e$, $e'$라고 함.
  • 에피폴라 plane과 두 이미지 평면의 교차하는 선 (파랑색 선)을 에피폴라 line이라고 함.
• 이미지 평면이 서로 평행하게 되면 밑의 사진과 같은 에피폴라 기하학을 만듦.
  
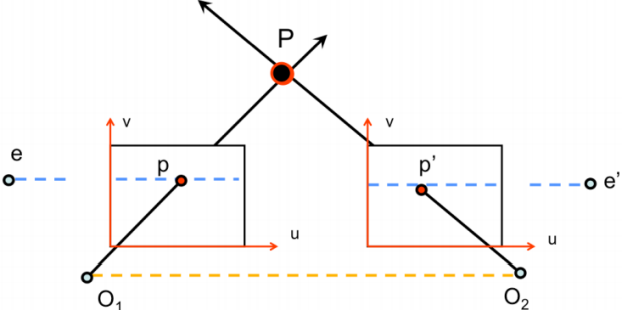
  • baseline이 이미지 평면과 평행하기에 (baseline과 각 이미지 평면의 교점이 없으므로) epipoles $e$와 $e'$가 무한대에 위치함.
  • 또한, 에피폴라 선이 이미지 평면의 u축과 평행함.
  • 이는 추후 image rectification 섹션에서 다룰 것임.
• 우리가 사진을 찍을 때, 실제 3D 위치 P에 대한 정확한 정보를 알 수 없음.
• 하지만, 이미지 평면에서 P에 대한 p점을 결정할 수 있으며, 우리가 카메라 위치, 방향 및 camera matrix에 대해 알고 있을 때,

  • $O_1$, $O_2$와 이미지 점 p을 통해 에피폴라 평면을 정의할 수 있으며, 이를 통해 에이폴라 선 역시 정의할 수 있음.

  • 또한, $p'$ 역시 $p'$의 이미지 에피폴라 선 위에 위치함.

    이를 통해, 두 이미지 간에 constraint를 만들 수 있음.

• 포인트와 에피폴라 선을 매핑하는 방법을 알아보자.
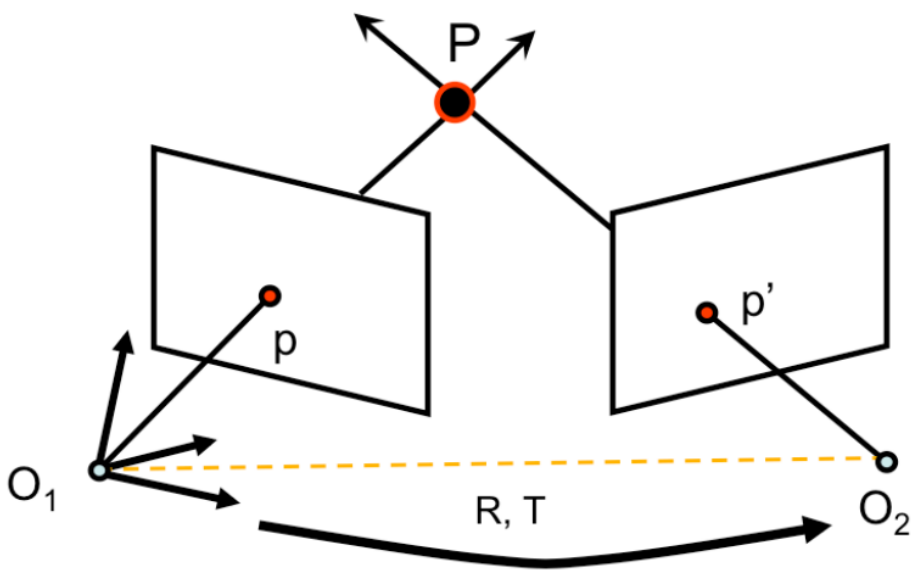
  • 3D 점을 각 이미지 평면의 위치로 매핑하는 camera projection matrix를 $M$, $M'$이라고 정함.
  • 또한, world reference system이 첫 번째 (M) 카메라에 연결되고, 두 번째 카메라는 회전과 rotation $R$ 이후, translation $T$에 의해 offset된다고 가정.
  • 이를 통해 camera projection matrix는 다음과 같이 정의됨.
    $M = K\begin{bmatrix} I & 0 \end{bmatrix}, M' = K'\begin{bmatrix} R^T &-R^TT \end{bmatrix}$
    • $M=K[I∣0]$이고 $M'=K'[R∣T]$이므로 M’에서 $M$으로의 변환은 $M =RM'+T$이고, $M' = R^T(M-T)$ = $[R^T -R^TT]$임.

3. The Essential Matrix

• 간단하게 하기 위해 우리가 canonical camera (표준 카메라)를 통해 촬영을 했다고 가정하자. 이 경우에 $K = K' = I$ 이다.
• 따라서 위 식은 다음처럼 간단하게 할 수 있고,
  $M = \begin{bmatrix} I & 0 \end{bmatrix}, M' = \begin{bmatrix} R^T &-R^TT \end{bmatrix}$
  이로 인해 $p'$의 위치가 world reference system이 연결된 첫 번째 카메라에서 $Rp'+T$로 나타낼 수 있음.
  
• 벡터 $Rp'+T$와 $T$가 에피폴라 평면에 위치하므로
  • 이 두 벡터의 외적을 계산하면 ($T$끼리의 외적은 0)
    $T × (Rp'+T) = T × Rp'$
    에피폴라 평면에 수직인 벡터를 얻게 됨.
    
  • 또한, 에피폴라 평면에 있는 점 $p$는 $T × Rp'$에 수직이므로 이 둘의 내적이 0이여야 함.
    $p^T ⋅[ T × Rp'] = 0 -----(3)$
    • 선형대수에서 두 벡터의 외적을 다음처럼 행렬-벡터 곱으로 표현 가능
      $a × b = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \\ \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = [a_×]b$

      • 식 유도

        $\mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} = (a_y b_z - a_z b_y) \mathbf{i} - (a_x b_z - a_z b_x) \mathbf{j} + (a_x b_y - a_y b_x) \mathbf{k} = \begin{bmatrix} a_y b_z - a_z b_y \\ a_z b_x - a_x b_z \\ a_x b_y - a_y b_x \end{bmatrix}$

        이고 이걸 행렬로 나타내면 됨.

  • 식 3에 이를 활용하면, $p^T ⋅[ T_×]( Rp') = 0$이 됨.
• 이때, $[ T_×]R$ 을 Essential Matrix $E$라고 하며, 이는 epipolar constraint을 간소화함.
  $p^TEp'=0$
• Essential Matrix $E$는 5개의 자유도를 가지는 3*3 행렬이며, rank가 2이고 singular Matrix이다.
  • 이 행렬은 $p$와 $p'$에 대한 에피폴라 선 계산에 사용됨.
    • 예를 들어, $l' = E^T p$는 두 번째 카메라의 이미지 평면에서 에피폴라 선이고,
    • $l = E p'$는 카메라 1의 이미지 평면에서 에피폴라 선임.
  • 또한 이 행렬의 중요한 속성은 epipole에 대한 내적이 0임. ($E^Te=Ee'=0$)
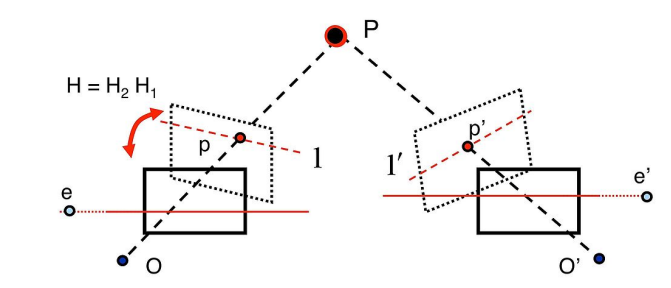
    • 즉, 카메라 1의 이미지에서 epipole 𝑒 외의 모든 점 𝑥에 대해 카메라 2의 이미지에서 대응하는 에피폴라 선 $𝑙' = 𝐸^𝑇x$는 epipole 𝑒 ′을 포함
      • 말이 좀 어려운데, 크게 두 개로 나누면
        1. 카메라 1에서 한 점 x는 정확히는 모르지만, 카메라 2의 에피폴라 선 $𝑙'$ 중 한 점에 대응되고,
        2. 이 에피폴라 선 $𝑙'$은 epipole $𝑒'$를 포함함. (두 번째 사진 참고)
    • 따라서, $e'^T(E^Tx)=(e'^TE^T)x=0$을 만족함.

4. The Fundamental Matrix

• 우리는 ****지금껏 canonical camera를 가정하여 $p$, $p'$관계를 도출했지만, 그렇지 않다면?
• $p_c=K^{−1}p$, $𝑝_𝑐'=𝐾'^{−1}𝑝'$ (c = canonical camera)가 될 것이고, $p^T_c ⋅[T_×]Rp'_c = 0$에 이를 대입하면
  $p^TK^{−T}[T_×]RK'^{−1}p'=0$
  이 도출됨.
  
• 여기서 $K^{−T}[T_×]RK'^{−1}$을 Fundamental Matrix이라고 함. (즉, $F =K^{−T}EK'^{−1}$ )
  • Fundamental Matrix은 ***Essential Matrix처럼 33 행렬이며, Rank가 2이고 singular Matrix이다.
  • Essential Matrix와 비슷하지만, Fundamental Matrix는 자유도가 7이며, $K$, $K'$정보를 포함하고, 이 행렬을 통해 카메라 행렬 𝐾, 𝐾’와 변환 𝑅, 𝑇를 몰라도 𝑝와 𝑝 ′에 대한 에피폴라 선을 계산 가능 ($l' = F^T p$, $l = Fp'$)
  • 또한, $Fe' = 0$, $F^T e = 0$을 만족함.
• Fundamental Matrix을 알면, 이미지의 한 점만 알고 있어도 대응하는 다른 이미지의 점에 대한 constraint (the epipolar line)을 구할 수 있음.
  • 따라서 $F$는 3D reconstruction, Multi-view object/scene matching에 사용할 수 있는 매우 강력한 도구임.

4.1 The Eight-Point Algorithm

• 하지만, 이 F를 얻는 것을 쉽지 않다. 하지만, 동일한 장면의 두 이미지를 가지고 카메라의 파라미터을 모른 채로 Fundamental Matrix을 얻는 Eight-Point Algorithm이 있다.
• 이는 두 이미지 사이에 최소 8쌍의 대응점을 알고 있다는 가정을 함.
• 각 대응점 $p_i = (u_i, v_i, 1)$과 $p'_i = (u'_i, v'_i, 1)$은 $p^T_iFp'_i=0$를 만족함. 이 식은 다음과 같이 재구성할 수 있음.
  $\begin{bmatrix} u_i u_i' & v_i' u_i & u_i & v_i'v_i & v_iv_i' & v_i & u_i' & v_i' & 1 \end{bmatrix}\begin{bmatrix} F_{11} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33} \end{bmatrix} = 0$
  • 식 유도
    $p_i^T F p'_i = \begin{bmatrix} u_i & v_i & 1 \end{bmatrix} \begin{bmatrix} F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33} \end{bmatrix} \begin{bmatrix} u'_i \\ v'_i \\ 1 \end{bmatrix}\\ = u_i u'_i F_{11} + u_i v'_i F_{12} + u_i F_{13} + v_i u'_i F_{21} + v_i v'_i F_{22} + v_i F_{23} + u'_i F_{31} + v'_i F_{32} + F_{33} = 0$
    • 이를 벡터로 표현.
• 3×3 행렬인 Fundamental Matrix에서 임의의 수인 scale 파라미터를 제외하면 이런 조건이 8개 필요함.
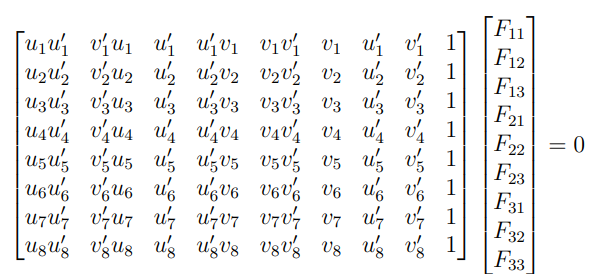
  • 이를 간단하게 표현하면 $Wf = 0$.
    • $W$는 8개 (이상의) 점으로부터 유도된 N × 9 행렬이고, f는 Fundamental Matrix의 요소들임.
• SVD를 통해 최적 행렬 $f$를 찾기 위해 다음 조건을 만족해야 함.
  $\underset{m}{\text{minimize}} \space ||F - \hat F||_F \space \space\space subject \space to \space \space \space det F = 0$
• SVD을 통해 $\hat F$ $= U\Sigma V^T$를 얻으면 full rank 즉, rank = 3인 $\hat F$를 얻게 되지만, $F$의 Rank는 2이므로 approximation 방법을 사용하여 F를 얻음.
  $F = U\begin{bmatrix} \Sigma_1 & 0 & 0 \\ 0 & \Sigma_2 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} = 0$

4.2 The Normalized Eight-Point Algorithm

• 위와 같은 standard least-squares 접근은 사실은 정확하지 않음. (p_i와 이에 대응하는 $\ell_i = F p'_i$ 사이의 거리가 10 픽셀 정도로 차이남.)
• 이를 줄이기 위해 Normalized Eight-Point Algorithm을 사용.
• 기존 접근에서 F를 구하기 위해 W가 SVD에 맞지 않음. (ill-conditioned)
  • SVD가 제대로 작동하기 위해, W의 특이값이 0 이거나 0에 가까운 점을 가지고 있어야 하고, 다른 값들은 0이 아니여야 함.
  • 하지만, 현대 카메라들은 픽셀이 매우 크기에 매우 큰 특이값과 상대적으로 작은 나머지 특이값을 가지게 됨.
• 이를 해결하기 위해 이미지 포인트들을 정규화함 (translation 및 scaling을 적용)

  1. 새로운 좌표계의 원점이 이미지 포인트 중심에 위치하게 함. (translation)

  2. 변환된 포인트의 mean square distance가 2 픽셀이어야 함. (scaling)

     $(\frac{2N}{\Sigma^N_{i = 1} ||x_i -\overline x||^2})^{1/2}$
• 이를 통해 다음처럼 나타낼 수 있음 (T는 transformation matrices)
  $q_i = Tp_i \space \space \space q_i' = T'p'_i$
• 이제 이를 통해 8점 알고리즘으로 새로운 $𝐹_𝑞$ 를 계산하고 이를 다시 비정규화함.
  $F = T^TF_qT$
  • 이 F는 real-world applications에 사용할 수 있음.

5. Image Rectification

• 두 이미지가 서로 평행한 경우를 알아보자.
• 두 카메라가 동일한 K를 가지고 있고, 카메라 사이에 회전이 없다.($R = I$)
• Essential Matrix을 계산할 때, 두 카메라가 x축을 따라 이동한다고 가정하면, $T = (T_x, 0, 0)$이므로
  $E = [T_×]R = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \\ \end{bmatrix}$
  이렇게 됨. (헷갈리면 위에 a, b 행렬-벡터 곱 표현 참고하기)
  
• Essential Matrix을 알기에 이미지 평면의 점에 대한 에피폴라 선의 방향을 찾을 수 있음.
  • $p'_0$와 관련된 에피폴라 선 $\ell$의 방향을 계산해보자.
    $\ell = Ep' = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \\ \end{bmatrix}\begin{bmatrix} u' \\ v' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ -T_x \\ T_xv'\\ \end{bmatrix}$
    • $v'$도 이렇게 구할 수 있고, 이 $v$와 $v'$이 에피폴라 선은 수평함.
      $(u \space \space v \space \space 1)\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \\ \end{bmatrix}\begin{bmatrix} u' \\ v' \\ 1 \\ \end{bmatrix} = (u \space \space v \space \space 1) \begin{bmatrix} 0 \\ -T_x \\ T_xv'\\ \end{bmatrix} = 0$
      이므로 $Tv = Tv' \space -> v = v'$ 즉, 수평하다.
      
• 이 수평함은 $p$와 $p'$ 사이의 계산에 편리함을 제공함.
• 따라서 두 이미지를 평행하게 만드는 Image Rectification은 이러한 유용성을 만들기 위함임.
• Image Rectification을 위해 카메라 매트릭스 $𝐾 , 𝐾'$ 나 두 카메라 사이의 상대 변환 $𝑅 , 𝑇$를 알 필요 없음.
• 대신 정규화된 8점 알고리즘으로 추정된 fundamental matrix을 사용하여 시작함.
• fundamental matrix을 이용하여 $p_i, p_i'$의 에피폴라 선 $\ell_i$, $\ell’_i$을 계산하고 (점마다 에피폴라 선이 존재) 이 에피폴라 선을 통해 각 이미지의 에피폴 $e, e'$를 추정. (에피폴은 에피폴라 선에 교차하므로)
  • 하지만, 실제로는 노이즈 때문에 에피폴라 선과 점의 least squared error를 최소화하여 찾음.
• 에피폴라 선은 에피폴라 선 위에 있는 모든 점에 대해 $[x|\ell^TX = 0]$을 만족하고, 이때 $\ell_i = [\ell_{i,1}, \ell_{i,2}, \ell_{i,3}]^T$으로 정의하면,
  $\begin{bmatrix} \ell^T_1 \\ ⋮ \\ \ell^T_n\\ \end{bmatrix}e = \begin{bmatrix} \ell_{1,1} & \ell_{1,2} & \ell_{1,3} \\ \ell_{2,1} & \ell_{2,2} & \ell_{2,3} \\ ⋮ & ⋮ & ⋮\\ \ell_{n,1} & \ell_{n,2} & \ell_{n,3} \\ \end{bmatrix} \begin{bmatrix} e_1 \\ e_2 \\ e_3 \end{bmatrix} =0$
  이와 같고, 이를 SVD로 풀면, 에피폴 $e$를 얻을 수 있음.
  
• 이렇게 얻은 $e$, $e'$는 수평이 아니므로 수평을 만들기 위해 homographies $H_1$, $H_2$를 사용함.
• 에피폴 $e'$를 무한대의 수평축 점 $(f, 0, 0)$에 매핑하는 $H_2$를 먼저 찾아보자. (두 번째 이미지에 대한 호모그래피)
• 호모그래피는 이미지 중심 점에 translation와 rotation을 적용하는 것과 같음.
  • 첫 번째로 이미지의 중심이 homogeneous coordinate (0,0,1)에 있도록 두 번째 이미지를 변환 (뒤에 있는 다른 변환들을 간단히 하기 위해)

    • 이미지 중심은 ($\frac{width}{2}$, $\frac{height}{2}$)이므로 translation matrix은 다음과 같다.

      $T = \begin{bmatrix} 1 & 0 & -\frac{width}{2} \\ 0 & 1 & -\frac{height}{2} \\ 0 & 0 & 1 \\ \end{bmatrix}$
  • 이제 회전을 적용하여 에피폴을 $(f, 0, 1)$지점에 위치시킴.
    • translation 적용된 에피폴 $Te'$이 $(e'_1, e'_2, 1)$에 위치한다고 하면,
      $R = \begin{bmatrix} \alpha \frac{e'_1}{\sqrt{e_1^{'2} + e_2^{'2}}} & \alpha \frac{e'_2}{\sqrt{e_1^{'2} + e_2^{'2}}} & 0 \\ -\alpha \frac{e'_2}{\sqrt{e_1^{'2} + e_2^{'2}}} & \alpha \frac{e'_1}{\sqrt{e_1^{'2} + e_2^{'2}}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \space \space \text {where} \space \alpha = \begin{cases} 1 &\text{if } \space e'_1 ≥ 0 \\ -1 &\text{if } \space otherwise \end{cases}$
      이와 같다.
      
  • 마지막으로 $(f, 0, 1)$에 놓인 점을 무한대의 수평축 점 $(f, 0, 0)$으로 보내기 위해 다음의 변환을 적용.
    $G = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -\frac{1}{f} & 0 & 1 \end{bmatrix}$
• 이를 통해 무한대의 에피폴을 얻을 수 있다. 이를 다시 이미지 공간으로 변환해야 하므로 $T^{-1}$를 적용하여 호모그래피 $H_2$를 다음과 같이 정의 (계산 편의를 위해 이미지를 (0,0,1)로 보낸것을 다시 돌려놓음)
  $H_2 = T^{-1} G R T$
• 이제 첫 번째 이미지에 맞는 호모그래피 $H_1$를 찾아보자. 이를 위해 이미지 간의 대응점 사이의 제곱 거리 합을 최소화하는 변환 $𝐻_1$을 찾음.
  $\arg \min_{H_1} \sum_{i} || H_1 p_i - H_2 p'_i ||^2 ---- (24)$
• 이는 $H_1 = H_A H_2 M$와 같음.
• 이것을 증명해보자. (이 밑부터 이해가 안됩니다..)
  • 먼저 M을 알아보자. 임의의 skew-symmetric matrix는 $A$ = $A^3$이므로 $F = [e]_\times M$이라 할 때, 다음과 같음.
    $F = [e]_{\times} M = [e]_{\times}[e]_{\times}[e]_{\times} M = [e]_{\times}[e]_{\times} F$
  • 이를 통해 $M = [e]_\times F$을 알 수 있음 (?)
  • $M$에 임의의 배수 $e$ 가 더해지더라도, $F = [e]_\times M$는 성립하므로 다음을 만족함.
    $M = [e]_{\times} F + e v^T$
    • 여기서 $v$는 임의의 벡터이고, $v^T = [1, 1, 1]$일 경우 잘 작동함.
  • 이제 $H_A$를 계산해보자.
    $H_A =\begin{bmatrix}a_1 & a_2 & a_3 \\0 & 1 & 0 \\0 & 0 & 1\end{bmatrix}$
    이고, 우리는 식 24을 만족하는 $H_1$, $H_2$를 찾는 것이 목적임. 이미 $𝐻_2$와 $M$ 값을 알고 있으므로 $\hat 𝑝'_𝑖 = 𝐻_2𝑀𝑝_𝑖$ 및 $\hat 𝑝'_𝑖=𝐻_2p'_i$ 을 대입하면,
    $\arg \min_{H_A} \sum_i \| H_A \hat{p}_i - \hat{p'}_i \|^2$
    이 됨. 특히, $\hat{p}_i = (\hat{x}_i, \hat{y}_i, 1)$ 및 $\hat{p'}_i = (\hat{x'}_i, \hat{y'}_i, 1)$으로 두면 이 최소화 문제는 다음처럼 됨.
    $\arg \min_{a} \sum_i \left( a_1 \hat{x}_i + a_2 \hat{y}_i + a_3 - \hat{x'}_i \right)^2 + \left( \hat{y}_i - \hat{y'}_i \right)^2$
  • 이때, $\left( \hat{y}_i - \hat{y'}_i \right)^2$는 상수 값이므로 다음처럼 단순화 됨.
    $\arg \min_{a} \sum_i \left( a_1 \hat{x}_i + a_2 \hat{y}_i + a_3 - \hat{x'}_i \right)^2$
  • 이는 W, b가 다음과 같을 때, a에 대한 least-squares인 $Wa = b$를 풀어야하는 문제임.
    $W = \begin{bmatrix} \hat{x}_1 & \hat{y}_1 & 1 \\ \vdots & \vdots & \vdots \\ \hat{x}_n & \hat{y}_n & 1 \end{bmatrix} \text{ and } b = \begin{bmatrix} \hat{x'}_1 \\ \vdots \\ \hat{x'}_n \end{bmatrix}$
  • $a$를 계산한 후, 우리는 $H_A$를 계산할 수 있으며 최종적으로 $H_1$을 구할 수 있음.