1. Introduction

• Camera Model에서 우리는 3D world를 digital image로 변환하는 법에 대해 배웠다
  • 카메라 파라미터, Calibration 등
• 이 강의에서는 카메라의 특성을 알고 있을 때, single image를 통해서 3D world의 구조를 복원하는 법과 single image에서 어떤 정보를 추론할 수 있는 지 알아보자.

2. Transformations in 2D

• 먼저 2D 공간에서 다양한 변환에 대해 알아보자.
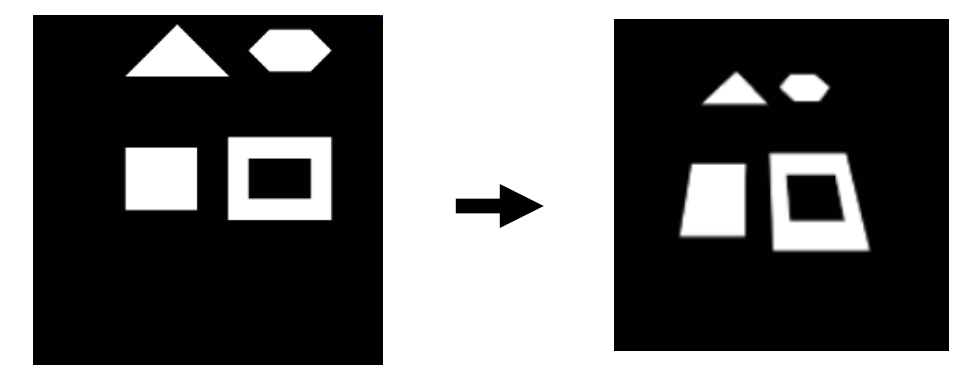
• Isometric transformations은 거리를 유지하는 변환으로 물체의 움직임을 조절함. 가장 기본적인 형태로 rotation $R$과 translation $t$로 이뤄짐.
  $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y\\ 1 \end{bmatrix}$
  
  • 여기서 $[x′,y′,1]^T$는 Isometric transformations 후의 point.
  • 3개의 자유도를 가짐.
• Similarity transformations은 길이 비율과 각도를 유지하는 변환임. Isometric transformations에서 scaling을 포함한 것. (Isometric transformations는 scale이 1인 Similarity transformations로 볼 수 있다.)
  $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} SR & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y\\ 1 \end{bmatrix} , S = \begin{bmatrix} s & 0 \\ 0 & s \\ \end{bmatrix}$
  
  • 4개의 자유도를 가짐.
• Affine transformations은 면적 비율, 선 길이 비율, 평행성을 유지하는 변환임. 임의의 벡터 $v$에 대해 아핀 변환 $T$는 다음과 같다. $T(v) = Av +t$ (A는 $\reals^n$ 선형 변환). Homogeneous coordinate에서 표현은 다음과 같다.
  $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y\\ 1 \end{bmatrix} = H_a\begin{bmatrix} x \\ y\\ 1 \end{bmatrix}$
  
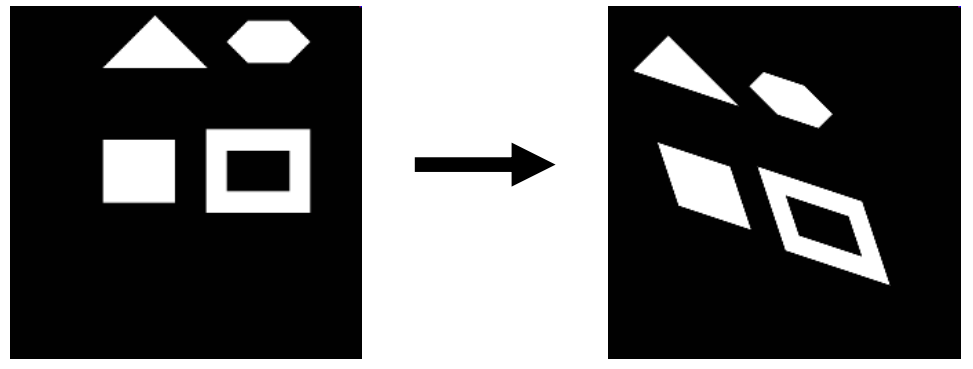
  • Similarity transformations는 아핀 변환의 한 종류로 볼 수 있음.
  • 6 자유도를 가짐.
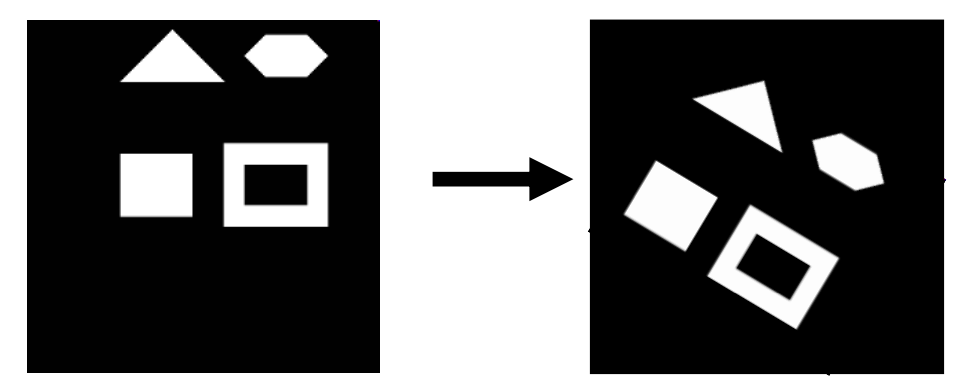
• Projective transformations (homographies)는 직선을 직선으로 맵핑하는 변환이지만, 평행성을 반드시 유지하지는 않음. 대신 점의 공선성(collinearity)을 유지하게 해줌. (즉, 점이 같은 선상에 있음을 보장함.)
  $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ v & b \end{bmatrix} \begin{bmatrix} x \\ y\\ 1 \end{bmatrix}$
  
  • 아핀 변환의 더 일반화된 형태임.

3. Points and Lines at Infinity

• 이미지의 구조 결정에 직선은 매우 중요하므로 2D와 3D에서의 직선에 대해 알아보자.
• 2D에서 직선은 $ax+by+c = 0$으로 나타내고 이를 homogeneous vector로 나타내면 $\ell = [a \space b \space c]^T$ 이다.
  • 일반적으로 다음과 같이 정의됨.
    $\forall p = \begin{bmatrix} x \\ y \end{bmatrix} \in \ell, \space \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0$
• 두 직선 $\ell$, $\ell'$이 한 점 $x$에서 교차할 때, 이 점은 $\ell$과 $\ell'$의 cross product(외적)로 정의됨.
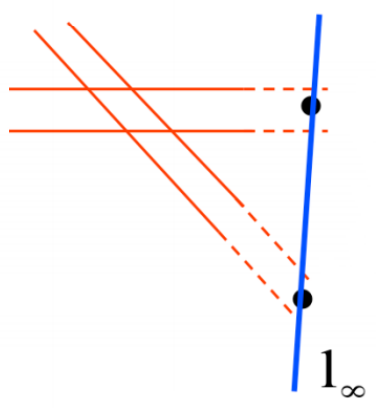
• 평행선 경우에는 일반적으로 교차하지 않는다고 생각하지만, 무한대에서 교차한다고 할 수 있음. (철로를 사진 찍으면 실제 3D 세계에서는 평행하지만, image에서는 한 점에 모이는 현상을 말하는 듯)
  • homogeneous coordinates에서 무한대의 점은 $[x \space y \space 0]^T$ 으로 나타낼 수 있음. (유클리드 좌표을 얻기 위해 마지막 0으로 나누면, $x$, $y$가 무한이므로)
    • 두 평행선 $\ell$, $\ell'$를 고려해보자. 두 선이 평행할 때, 기울기가 같고, 교점을 두 직선의 cross product로 구한다 했으므로 $x$는 교점은 다음과 같다.
      $\ell × \ell' ∝ \begin{bmatrix} b \\ -a \\ 0 \end{bmatrix} = x_\infty$
    • 이 점을 ideal point(이상점)이라고 함. $-\frac{a}{b}$의 기울기를 가지는 모든 평행한 직선은 이 ideal point에서 만난다.
      $\ell^Tx_\infty = \begin{bmatrix} a & b & c\end{bmatrix} \begin{bmatrix} b \\-a \\c \end{bmatrix} = 0$
• 이러한 무한대 개념은 lines at infinity을 정의하는데 사용될 수 있음.
  • n개의 평행선이 있다고 가정해보자. 각 평행선 쌍은 $[x_{\infty,1}, ..., x_{\infty,n}]$ 점에서 교차함.
  • 이 점들을 통과하는 직선 $\ell_{\infty}$은 모든 $i$에 대해($∀i$), $\ell^T_{\infty}x_{\infty, i}$ $= 0$를 만족하며 이는 $\ell_{\infty}$$= [0, 0, c]^T$을 의미함. 이때, c는 임의의 값이므로 $\ell_{\infty}$$= [0, 0, 1]^T$로 정의할 수 있음.
• 무한대의 점 $p_{\infty}$에서 Projective transformation $H$을 적용하면?
  $p' = Hp_{\infty} = \begin{bmatrix} A & t \\v & b\end{bmatrix}\begin{bmatrix} 1 \\1 \\ 0\end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y\\ p'_z\end{bmatrix}$
  • 마지막 점이 0에서 변환 후 $p'_z$가 되었으므로 Projective transformation이 무한대의 점을 무한대가 아닌 점으로 맵핑하는 것을 뜻함.
• 무한대의 점 $p_{\infty}$에서 Affine transformations을 적용하면?
  $p' = Hp_{\infty} = \begin{bmatrix} A & t \\0 & b\end{bmatrix}\begin{bmatrix} 1 \\1 \\ 0\end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y\\ 0\end{bmatrix}$
  • Affine transformations은 무한대의 점을 무한대로 맵핑
• 이제 Projective transformation $H$를 직선 $\ell$에 적용하여 새로운 직선 $\ell'$를 만들어보자. $\ell$의 모든 점 $x$가 $x^T\ell = 0$을 만족해야 함.
  • 항등 속성(identity property)을 이용하여 ($I = H^TH^{-T}$) 다음 식을 만들 수 있다.
    $x^TI\ell = x^TH^TH^{-T}\ell = 0$
    이때, Projective transformation은 직선을 직선으로 맵핑하는 변환이므로 새로운 직선 $\ell’$도 역시 $x'\ell'= 0$을 만족하므로
    $x^TH^TH^{-T}\ell = x'^T\ell'$
    이다. 또한, $x' = Hx$이고, $x^TH^T = (Hx)^T$이므로 $x'^TH^{-T}\ell = x'^T\ell'$로 변환할 수 있음. 즉, $H^{-T}\ell = \ell'$임을 알 수 있다.
    

4. Vanishing Points and Lines

• 지금까지 2D에서의 무한대 점과 직선의 개념을 배웠다. 이제 3D로 확장해보자.
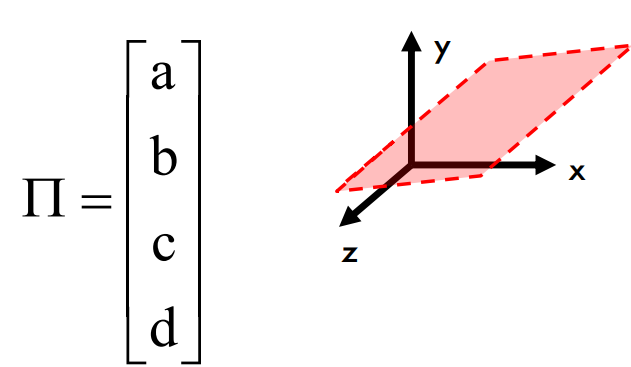
• 이 3D에서는 planes $Π$이라는 개념을 도입함.

  • 이 planes $Π$을 벡터 $[a, b, c, d]^T$로 나타낼 수 있으며,
    - (a, b, c)는 planes에 대한 법선 벡터를 형성하고, d는 원점에서 법선 벡터 방향으로 planes까지의 거리를 나타냄.

    $x^T\begin{bmatrix} a \\ b\\ c \\d \end{bmatrix} = ax_1+bx_2+cx_3+d =0$

• 3D에서 직선은 두 평면의 교차로 정의되며 절편 위치(intercept location)와 3개 차원의 각 기울기로 4개의 자유도를 가짐.
  
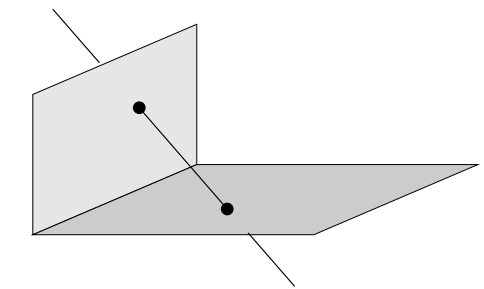
  • 각 평면 상의 점을 통해 4개의 자유도를 가짐.
• 점은 2D와 비슷하게 정의됨. 무한대에 있는 점은 평행선의 교차점으로 정의됨.
  • 또한, $x_{\infty}$에 있는 점에 Projective transformation을 적용하면 더 이상 무한대에 있지 않은 점 $p_{\infty} = \begin{bmatrix} p_1 \\ p_2\\ p_3 \end{bmatrix}$가 생김. 이를 vanishing point이라고 부름.
• 이 vanishing point을 통해 무엇을 할 수 있을까?
• 3D의 평행선, image에서의 corresponding vanishing(대응 소실점), 그리고 카메라 파라미터 K, R, T (intrinsic parameters인 K, extrinsic parameters인 회전 행렬 R, 변환 행렬 T)의 관계를 도출해보자.
  • camera reference system에서 3D 평행선들의 집합의 방향 벡터 d = (a, b, c)가 있을 때, 이 선들은 무한대의 점에서 교차하며, 이를 image로 투영하면 vanishing point $v$가 생성됨.
  • $x_{\infty} = \begin{bmatrix} a \\ b\\ c \\ 0 \end{bmatrix}$ 일 때, $v=Mx_{\infty} = K[I \space 0]\begin{bmatrix} a \\ b\\ c \\ 0 \end{bmatrix} = K \begin{bmatrix} a \\ b\\ c \end{bmatrix}$이므로 $v$는 $v = Kd$로 정의되며 이 식을 통해 $d = \frac{K^{-1}v}{||K^{-1}v||}$를 도출할 수 있음.
• 평면 $Π$을 평행선 집합의 집합 즉, Superset이라고 간주하면, 각 평생선의 집합은 무한대에서 한 점에 교차함.
  • 이 무한대의 점들을 통과하는 직선은 lines at infinity인 $\ell_{\infty}$임.
  • 우리는 평면을 평행선 집합의 Superset으로 간주했으므로 이 직선은 평행한 두 평면이 교차하는 직선으로 정의됨. (바다 수평선 찍으면 이미지에서는 한 직선으로 모이는 것?)
• $\ell_{\infty}$에 Projective transformation을 적용하면 ‘무한대가 아닌 선’이 되고 이를 vanishing line(소실선) 또는 horizon line $\ell_{horiz}$라고 함.
  • 사진 출처 : https://mysketchjournal.com/how-to-draw-linear-perspective-without-vanishing-points/
  • 이 horizon line은 vanishing point들을 지나는 직선이며 다음과 같이 계산됨.
    $\ell_{horiz} = H^{-T}_P\ell_{\infty}$
    
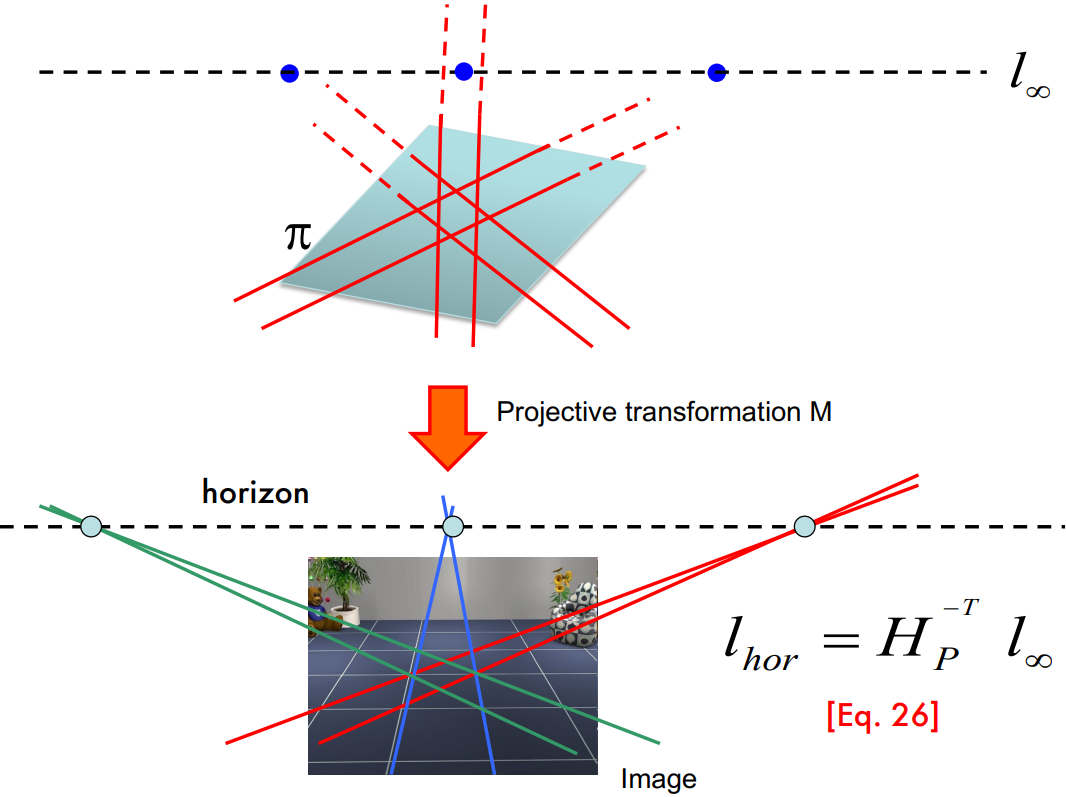
• $\ell_{horiz}$은 수학적으로 명확하지 않는 image의 특성을 추론할 수 있게 함.
  • 예를 들어, 위 사진처럼 이미지 좌표에서는 평행하지 않지만, 우리는 평행하다고 느끼는 이러한 특성을 추론할 수 있게 해줌.
• 또한, 3D에서의 평면의 법선 $n$과 이미지의 $\ell_{horiz}$ 사이에 관계를 도출 가능
  $n = K^T\ell_{horiz}$
  • 이는 우리가 vanishing line을 인식할 수 있고, camera calibration이 되었다면 평면 $Π$의 방향을 추정할 수 있음.
• plane at infinity $Π_{\infty}$라는 개념도 있음.
  • 이 평면은 두 개 이상의 vanishing point에 의해 정의되며, Homogeneous coordinate에서는 벡터 $[0, 0, 0, 1]^T$로 표현됨.
    
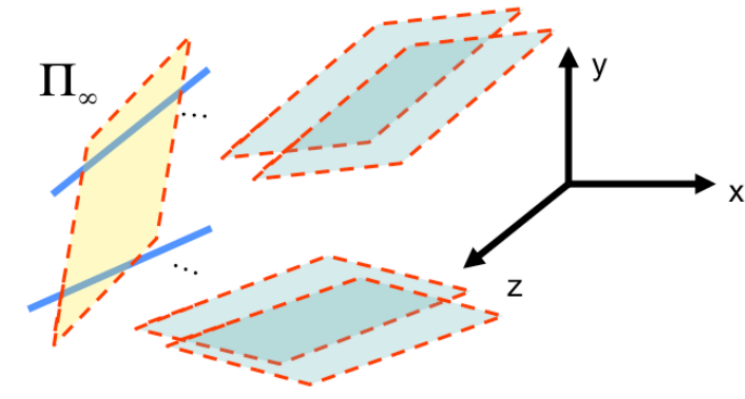
    • 2개 (이상)의 vanishing lines (파랑선)으로 $Π_{\infty}$을 정의
• 3D에서 평행한 두 쌍의 선이 각각 $d_1$, $d_2$방향을 가지고, 무한대의 점 $x_{1,\infty}$, $x_{2,\infty}$에 대응한다고 하자. $v_1$, $v_2$가 vanishing point라고 할 때, $d_1$, $d_2$ 사이의 각도 $\theta$는 cosine law에 의해 다음과 같이 구해짐.
  $cos(\theta) = \frac{d_1 ⋅d_2}{||d_1|| \space ||d_2||} = \frac{v_1^Tωv_2}{\sqrt{v_1^Tωv_1}\sqrt {v_2^Tωv_2}}, \space \\(where \space ω = (KK^T)^{-1}, v_1 = Kd_1, v_2 = Kd_2) --- (12)$
  
  • 증명
    • $d_1 ⋅ d_2 = v_1^TK^{-T}K^{-1}v_2$이고 $ω = (KK^T)^{-1}$이므로 $d_1 ⋅ d_2 = v_1^Tωv_2$
• 이를 3D 평면으로 확장해보자
  • 모든 평면에 대해서 vanishing line $\ell_{horiz}$과 법선 $n = K^T\ell_{horiz}$을 구할 수 있으므로 각 평면의 법선 벡터 $n_1$, $n_2$ 사이의 각도를 계산하여 두 평면 사이의 각도 $\theta$을 결정할 수 있음.
  • vanishing line $\ell_1$ 과 $\ell_2$에 대해 $\theta$는 다음과 같음.
    $cos(\theta) = \frac{n_1 ⋅ n_2}{||n_1|| \space ||n_2||} = \frac{\ell_1^Tω^{-1}\ell_2}{\sqrt{\ell^T_1ω^{-1}\ell_1} \sqrt{\ell^T_2ω^{-1}\ell_2}}$

5. A Single View Metrology Example

• 3D 세계에서 두 개의 평면이 있는 이미지가 있고, 각 평면에서 평행한 선 한 쌍이 있다고 가정하자.
• 이 이미지에서 두 vanishing point $v_1,$ $v_2$를 추정할 수 있으며, 우리는 두 평면이 (건물 평면이) 90도로 수직이라는 것을 안다.
  • 이 경우, 식 (12)의 $v_1^Tωv_2$$=0$ 이다. 하지만, ω는 아직 알 수 없는 카메라 파라미터 $K$에 의해 결정됨.
• 이 두 vanishing point을 아는 것만으로 $K$를 추정할 수 있을까?
• K는 앞써 배웠던 것처럼 5개의 자유도를 가지고 있지만, 우리가 아는 것은 $v_1^Tωv_2=0$ 뿐이므로 불가능함.
• 따라서 또 다른 vanishing point이 필요하다. 밑 사진처럼 추가적인 vanishing point을 추정함.
  
  • 이를 통해 $\omega v_2 = v_1 \omega v_3 = v_2 \omega v_3 = 0$의 3개의 constraint을 알 수 있지만, 그래도 부족하다.
• 하지만 카메라가 zero-skew와 square pixels를 가진다는 가정을 하면
  $\omega = \begin{bmatrix} \omega_1 & \omega_2 & \omega_4 \\ \omega_2 & \omega_3 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6 \\ \end{bmatrix}$
  에서 zero-skew으로 skewness = $\omega_2$ = 0, square pixels (가로 세로 픽셀 비율이 동일) = $\alpha (\omega_1) = \beta (\omega_2)$이므로
  $\omega = \begin{bmatrix} \omega_1 & 0 & \omega_4 \\ 0 & \omega_1 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6 \\ \end{bmatrix}$
  가 됨.
  
• 또한, homogeneous coordinate는 scale-invariant하므로 scale 변수는 임의로 지정하여, 실제 변수는 세 개로 줄어 듦.
  
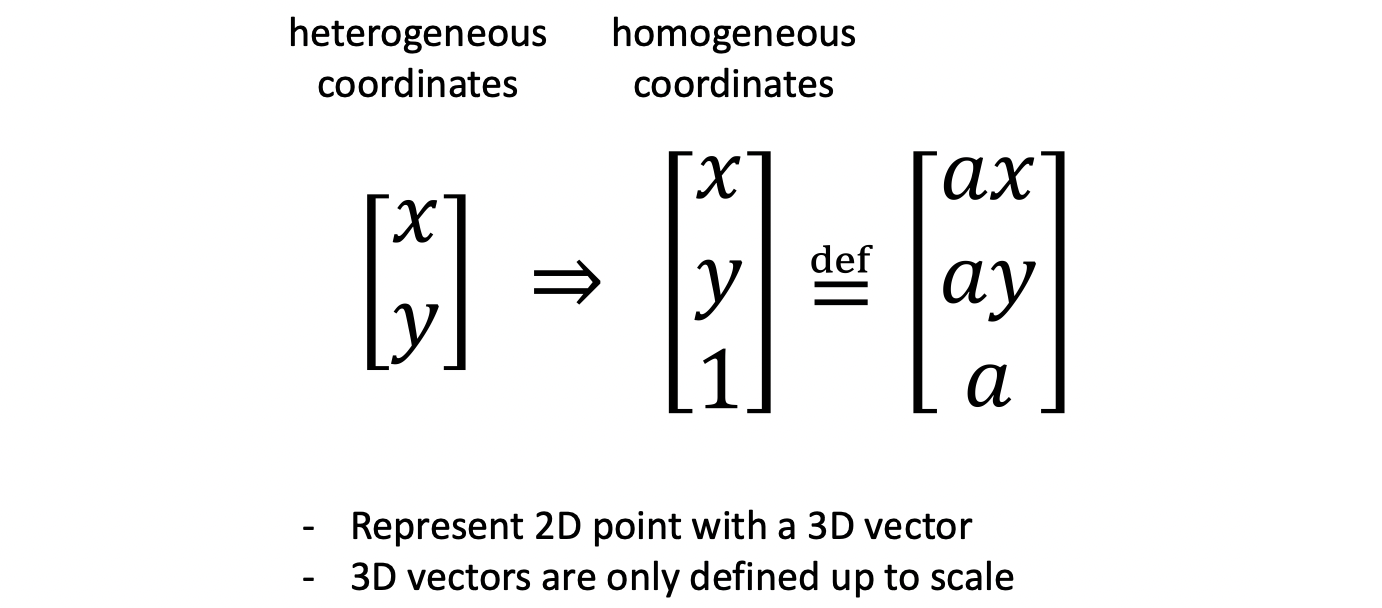
• 이렇게 구한 $\omega$를 통해 Cholesky 분해를 통해 K를 계산할 수 있음.
  • K를 알면, 모든 평면의 3D을 재구성할 수 있음.