전통적인 이미지 분류(Traditional Image Categorization)는 오늘날의 딥러닝 기반 인식 시스템이 등장하기 전, 컴퓨터 비전 분야에서 가장 기본적이면서도 핵심적인 연구 주제였다. 당시 접근법은 이미지 전체를 하나의 벡터로 표현하고, 통계적 혹은 기계학습 기법을 이용하여 범주(category)를 구분하는 방식이었다. 이 과정에서 중요한 점은 이미지를 직접 분류하기보다, 먼저 유용한 특징(feature)을 정의하고 추출해야 한다는 것이었다.
특징 추출과 표현
이미지 분류에서 가장 먼저 수행되는 단계는 특징 추출(feature extractioin)이다. 원본 픽셀 값(intensity나 color value)만으로는 고차원적이고 노이즈가 많아 효과적인 분류가 어렵기 때문에, 이미지의 본질적 특성을 잘 드러내는 특징 공간으로 변환한다. 예를 들어,
- 에지(edge)나 코너(corner)와 같은 국소(local) 특징
- 히스토그램(HOG, SIFT)과 같은 전역(global) 혹은 중간 수준의 특징
- 색상, 질감(texture) 등의 통계적 표현
이와 같은 특징들은 픽셀 수준의 정보를 요약하여, 분류기(classifier)가 학습 가능한 형태로 변환해준다.
전통적 학습 방법
특징 벡터로 표현한 후, 이를 학습 알고리즘에 입력하여 범주를 예측한다. 여기서 주로 사용된 방법들은 다음과 같다.
-
최근접 이웃(K-Nearest Neighbors, KNN) - 특징 공간에서 가장 가까운 데이터의 레이블을 그대로 예측
-
나이브 베이즈(Naïve Bayes) - 확률적 분포를 기반으로 클래스 추정
-
로지스틱 회귀(Logistic Regression) - 선형 결정 경계를 학습하여 이진 혹은 다중 분류 수행
-
서포트 벡터 머신(SVM) - 초평면(hyperplane)을 학습하여 고차원에서도 분리 가능한 결정 경계 제공
한계와 딥러닝으로의 전환
이러한 전통적인 방법들은 특징 추출과 분류가 분리되어 있다는 점에서 큰 제약을 가졌다. 즉, 특징은 사람이 설계(hand-crafted feature)해야 하며, 그 품질이 분류기의 성능을 좌우하였다. 따라서 복잡한 데이터나 대규모 데이터셋에서는 일반화가 어렵고, 객체의 다양한 변형(크기, 위치, 조명 변화)에 강인하지 못했다.
이 한계는 결국 딥러닝(Deep Learning)의 필요성을 불러왔으며, 합성곱 신경망(CNN)은 특징 추출과 분류를 하나의 모델 안에서 통합하여 학습할 수 있게 만들었다.
Feature Design
딥러닝이 등장하기 전까지 컴퓨터 비전에서 가장 중요한 과제 중 하나는 좋은 특징(feature)을 어떻게 설계할 것인가였다. 이미지를 그대로 사용하는 대신, 물체나 장면을 구분할 수 있는 핵심 패턴(에지, 코너, 질감 등)을 찾아내고 벡터로 표현하는 방식이 주류였다. 이를 Feature Design 혹은 Hand-crafted Feature라고 부른다.
주요 특징 설계 기법
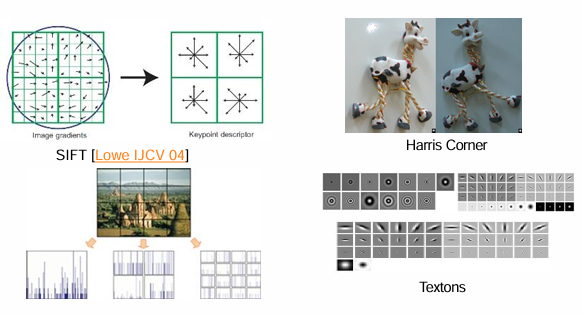
-
Harris Corner Detector
- 이미지에서 모서리(corner)는 강인한 특징으로, 시점 변화나 회전에도 비교적 잘 유지된다.
- Harris Corner는 픽셀 주변 윈도우를 여러 방향으로 이동시켰을 때 강한 변화가 있는 점을 코너로 정의한다.
- 예: 물체의 꼭짓점, 교차점 같은 지점.
수식 (코너 응답 함수):
- : 이미지 그래디언트 기반의 2x2 행렬
- : 경험적 상수 (보통 0.04 ~ 0.06)
-
SIFT (Scale-Invariant Feature Transform, Lowe 2004)
- 크기, 회전, 조명 변화에도 강인한 지역(local) 특징.
- 검출 단계: 스케일 공간에서 극값 탐색 → 키포인트 후보 추출.
- 기술 단계: 키포인트 주변의 그래디언트 방향 분포를 기반으로 벡터(128차원) 생성.
- 두 이미지 간 대응점 매칭(matching)에 널리 사용되었다.
-
Textons (Texture Primitives)
- 이미지의 질감을 나타내는 기본 단위.
- 다양한 필터(예: 가버 필터, DOG 등)를 적용하여 나온 응답 패턴을 텍스톤 벡터로 사용.
- 주로 재질(texture) 인식, 배경 분류 등에 활용.
특징 설계의 의의와 한계
-
의의:
- 시점, 조명, 크기 변화에 강인한 특징을 찾기 위해 다양한 수학적 아이디어가 제안됨.
- 객체 인식(Object Recognition), 영상 정합(Image Matching), 3D 복원 등 전통적 비전 과제에서 필수.
-
한계:
- 사람이 직접 어떤 특징을 쓸지 설계해야 하므로, 데이터와 문제에 따라 한계적임.
- 복잡한 패턴이나 높은 수준의 의미(예: “개”와 “고양이” 구분)는 설계된 특징만으로 포착하기 어려움.
이 때문에 이후 딥러닝 기반 접근법에서는 “특징 설계(Feature Design)” 대신 **특징 학습(Feature Learning)**이라는 패러다임으로 넘어가게 된다. CNN은 이미지로부터 특징을 자동으로 학습하므로, SIFT나 Harris와 같은 핸드크래프트 특징의 필요성을 크게 줄였다.
Hierarchical Feature Extraction
전통적인 Feature Design 접근에서 벗어나면서 연구자들은 특징을 사람이 설계하지 않고, 데이터로부터 자동으로 학습하는 방법을 모색하기 시작했다. 이 흐름은 인간의 시각 피질(Visual Cortex)에서 영감을 받아 발전했으며, 인공 신경망(Artificial Neural Network)과 딥러닝으로 이어졌다. 특히, Hubel과 Wiesel의 시각 피질 연구는 계층적 특징 추출(hierarchical feature extraction) 개념의 출발점이 되었다.
1. Biological Inspiration – Visual Cortex

David Hubel과 Torsten Wiesel의 연구에 따르면, 시각 피질에는 단순(Simple), 복합(Complex), 초복합(Hypercomplex) 세포가 존재한다.
- Simple cells: 특정 방향의 에지(edge)에 반응.
- Complex cells: 위치 변화에 강인하며, 조금 더 복잡한 패턴을 감지.
- Hypercomplex cells: 물체의 끝(edge endings)이나 코너 같은 더 고차원 특징에 반응.
즉, 저수준 특징(에지) → 중간 수준 특징(모양, 패턴) → 고수준 특징(객체)으로 이어지는 계층 구조를 통해 인간의 시각은 세상을 인식한다.
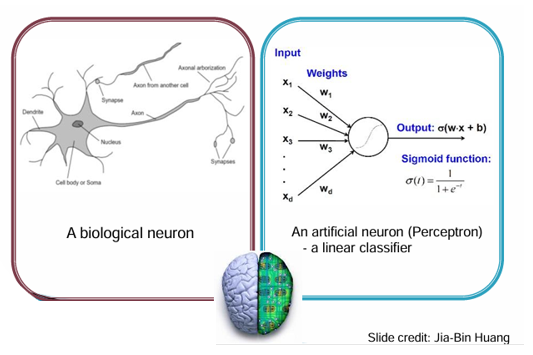
2. Artificial Neuron과 Perceptron
이 아이디어는 인공지능에도 적용되었다.
- Perceptron(1958, Rosenblatt)은 가장 단순한 형태의 인공 신경망으로, 입력 벡터에 가중치 를 곱해 선형 결정을 내리는 구조이다.
- 뉴런의 수와 층을 확장하면 더 복잡한 패턴을 학습할 수 있으며, 이는 곧 다층 퍼셉트론(MLP)으로 발전했다.
수식 (퍼셉트론 출력):
여기서 는 활성화 함수(예: sigmoid, ReLU 등)이다.
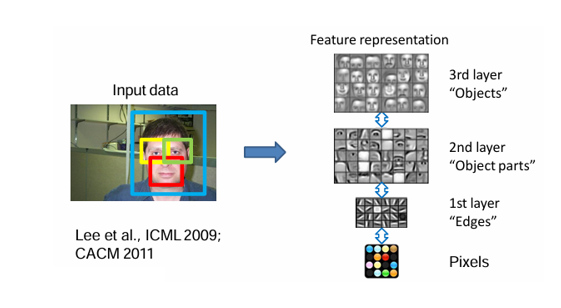
3. Hierarchy of Feature Extractors
현대 딥러닝의 핵심은 계층적 특징 추출(hierarchical feature learning)이다.

- Layer 1 (저수준 특징): 픽셀로부터 에지, 코너 같은 기초 패턴을 추출.
- Layer 2 (중간 수준 특징): 저수준 특징을 조합해 "부분 구조(object parts)"를 표현.
- Layer 3 (고수준 특징): 물체 전체, 사람 얼굴과 같은 객체 수준의 특징을 학습.
- 최종적으로 분류기(classifier)가 라벨을 예측.
이때 중요한 점은 모든 층을 독립적으로 설계하지 않고, 데이터를 통해 end-to-end 학습한다는 것이다.
4. 딥러닝으로의 연결
- 전통적 접근: 사람이 직접 SIFT, HOG, Harris Corner 같은 특징을 설계.
- 딥러닝 접근: 신경망이 계층적으로 특징을 자동 학습.
- 차이점: “Feature Design”에서 “Feature Learning”으로 패러다임이 변화.
정리하면, 딥러닝은 인간 시각 피질의 계층적 구조에서 영감을 받아, 픽셀 → 에지 → 객체 부분 → 객체 전체로 이어지는 특징 계층을 학습한다. 이는 전통적 컴퓨터 비전과 딥러닝 기반 인식의 본질적 차이를 보여준다.
Perceptron
1. Perceptron의 개념
- 퍼셉트론(Perceptron)은 인공 신경망(Artificial Neural Network) 가장 기본적인 모델이다.
- 입력(feature) 에 대해 가중치(weight) 를 곱하고, 이를 모두 합한 뒤, 활성화 함수(activation function)를 적용해 최종 출력을 얻는다.
- 생물학적 뉴런(Neuron)의 수상돌기 → 시냅스 가중치 → 축삭 신호 전송 과정을 단순화한 모델이다.
수식 표현
여기서 는 sign 함수(이진 분류) 또는 sigmoid/ReLU 같은 활성화 함수이다.
2. Perceptron 동작 원리
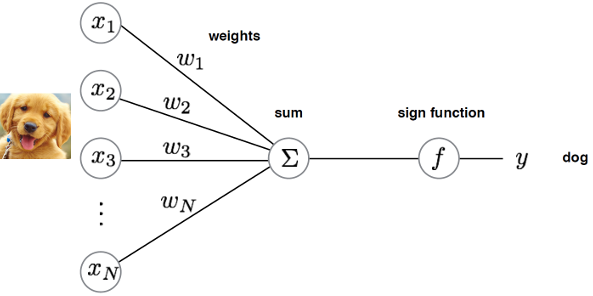
- 입력 (Input): 이미지 픽셀 값이나 특징 벡터.
- 가중치 (Weight): 각 입력 값의 중요도를 나타내며 학습을 통해 갱신된다.
- 합 (Summation): 모든 입력의 가중합을 계산.
- 출력 (Output): sign 함수 또는 sigmoid 함수 등을 적용하여 최종 클래스를 예측.
예: 강아지 사진 → “dog” 클래스
3. Linear Perceptron
퍼셉트론은 기본적으로 선형 분류기(linear classifier)이다.
- 만약 데이터가 선형적으로 구분 가능한 경우, 퍼셉트론은 항상 올바른 결정 경계(hyperplane)를 학습할 수 있다.
- 하지만 XOR 문제처럼 선형 분리가 불가능한 경우에는 단일 퍼셉트론으로 해결할 수 없다. 이 한계 때문에 다층 퍼셉트론(MLP)이 등장하게 된다.
4. Perceptron 학습 알고리즘 (Training Algorithm)
퍼셉트론은 가중치 업데이트 규칙을 통해 학습한다.
-
가중치 를 무작위로 초기화한다.
-
각 학습 샘플 에 대해 예측값 계산:
-
예측이 틀리면 가중치 갱신:
- : 학습률(learning rate)
- : 실제 라벨, : 예측값
이 과정을 여러 epoch 동안 반복하면서 분류 성능이 개선된다.
5. 의의와 한계
- 의의: 퍼셉트론은 “신경망으로 학습할 수 있다”는 것을 최초로 보여준 모델이다. 현대 딥러닝의 초석이 되었으며, 생물학적 뉴런과 인공지능을 연결하는 첫 시도였다.
- 한계: 단일 퍼셉트론은 비선형 문제(XOR 문제 등)를 해결하지 못한다. 이 한계를 극복하기 위해 다층 퍼셉트론(MLP) → CNN → 딥러닝으로 발전하게 된다.
요약하자면, 퍼셉트론은 신경망의 가장 기본 단위로, 입력을 가중합하여 활성화 함수를 통과시켜 출력을 생성한다. 비록 단일 퍼셉트론은 한계가 있지만, 이후 다층 구조로 확장되면서 현대 딥러닝의 시작점이 되었다.
Multi-layer Perceptrons (MLP)
1. 등장 배경
- 단일 퍼셉트론은 선형 분리(linearly separable) 문제만 해결 가능하다.
- 예를 들어, XOR 문제는 어떤 직선(혹은 초평면)으로도 데이터를 나눌 수 없기 때문에 단일 퍼셉트론으로는 학습할 수 없다.
- 이를 해결하기 위해 여러 개의 퍼셉트론을 층(layer)으로 연결한 다층 퍼셉트론(MLP)이 제안되었다.
2. 구조
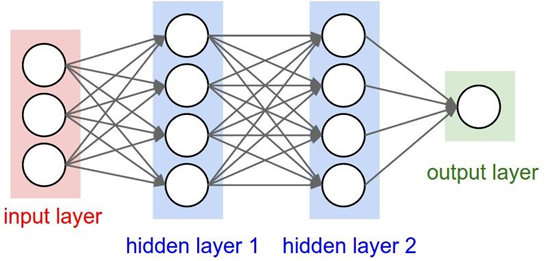
MLP는 크게 세 부분으로 이루어진다.
- 입력층 (Input Layer): 데이터의 특징 벡터 입력.
- 은닉층 (Hidden Layers): 여러 개의 퍼셉트론으로 구성되며, 비선형 활성화 함수를 적용해 복잡한 패턴을 학습한다.
- 출력층 (Output Layer): 최종 예측(class label 혹은 회귀 값).
- 은닉층이 여러 개 쌓이면, 모델은 점점 더 고차원의 특징을 학습할 수 있다.
- 이 구조는 이후 딥러닝(Deep Neural Network, DNN)의 기반이 되었다.
3. 비선형성의 도입 (Activation Function)
퍼셉트론을 단순히 여러 개 쌓는 것만으로는 여전히 선형 모델과 같다. 따라서 각 노드에는 비선형 활성화 함수가 필요하다.
대표적인 활성화 함수:
-
Sigmoid:
- 0~1 사이 값을 출력, 확률적 해석 가능.
- 하지만 기울기 소실(vanishing gradient) 문제가 있음.
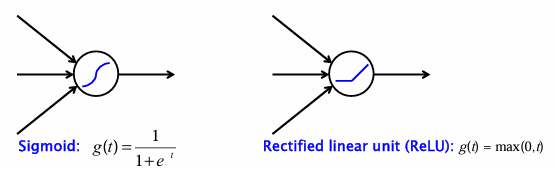
-
ReLU (Rectified Linear Unit):
- 계산이 간단하고, 깊은 네트워크 학습에 효과적이며.
- 현재 CNN 등 딥러닝 모델의 기본 활성화 함수로 자리 잡았다.
4. 학습 방법 (Training)
MLP는 학습 과정에서 오차(error)를 최소화하기 위해 가중치를 조정한다.
-
손실 함수 (Loss Function):
예측값과 실제 라벨 사이의 오차를 수치화. -
경사 하강법 (Gradient Descent):
가중치를 오차가 줄어드는 방향으로 업데이트.- : 학습률 (learning rate)
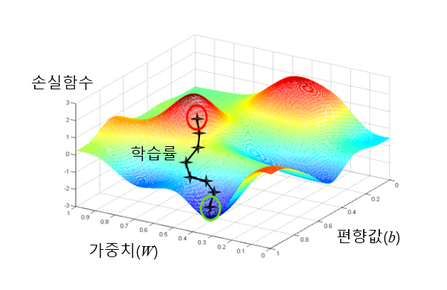
- : 학습률 (learning rate)
-
역전파 (Backpropagation):
- 오차를 출력층에서 입력층으로 전달하면서, 체인 룰(chain rule)을 이용해 각 층의 가중치 기울기를 계산.
- 모든 층을 동시에 학습 가능(end-to-end training).
-
확률적 경사 하강법 (Stochastic Gradient Descent, SGD):
- 데이터 전체가 아니라, 작은 배치(batch) 단위로 학습을 진행.
- 계산 효율을 높이고, 지역 최적해(local minima)를 피하는 데 도움.
5. MLP의 의의와 한계
-
의의:
- 비선형 문제를 해결할 수 있는 최초의 신경망 구조.
- 딥러닝의 기초 모델로, 이후 CNN, RNN 같은 다양한 아키텍처로 확장.
-
한계:
- 은닉층이 깊어질수록 학습이 어려워지는 기울기 소실 문제(vanishing gradient problem) 발생.
- 이미지와 같은 고차원 데이터에는 학습 효율이 떨어지며, 공간 구조(Spatial Structure)를 반영하지 못함.
- 이 한계를 극복하기 위해 합성곱 신경망(CNN)이 등장했다.
요약하자면, Multi-layer Perceptron은 단일 퍼셉트론의 한계를 극복하고 비선형 문제를 해결할 수 있게 만든 구조로, 딥러닝의 출발점이자 CNN으로 가는 징검다리 역할을 한다.
Network Capacity (모델 용량)
-
은닉층(hidden layer)의 뉴런 수가 많아질수록, 신경망은 더 복잡한 결정 경계(decision boundary)를 학습할 수 있다.
-
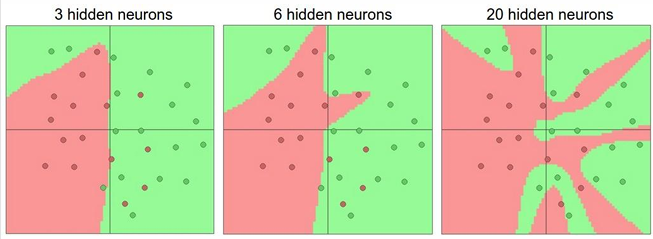
예시 그림에서 보듯이:
- 3개의 뉴런: 단순하고 매끄러운 경계 → 과소적합(underfitting) 가능성.
- 6개의 뉴런: 더 세밀한 경계 표현 가능.
- 20개의 뉴런: 매우 복잡한 경계 → 과적합(overfitting) 위험.
즉, 은닉층 크기는 모델의 표현력(capacity)을 결정하며, 데이터에 적합한 복잡도를 찾아야 한다.
Regularization (정규화)
과적합을 방지하기 위한 핵심 기법 중 하나가 정규화이다.
- 일반적으로 가중치 크기(weight magnitude)에 패널티를 부여한다.
- 목적 함수는 다음과 같이 표현된다:
여기서 는 정규화 계수.
- 가 작으면 (0.001) → 모델은 매우 복잡한 경계를 학습, 과적합 가능성↑.
- 가 크면 (0.1) → 모델은 단순한 경계만 학습, 과소적합 가능성↑.
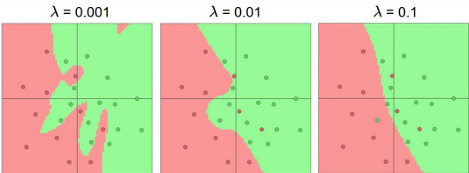
즉, 정규화는 모델이 데이터 전체에 고르게 의존하도록 유도하고, 일부 입력에 지나치게 의존하는 것을 방지한다.
Neural Networks: 장점과 한계
Pros (장점)
- 범용 함수 근사기 (Universal Function Approximator): 충분한 뉴런과 층이 있다면 어떤 함수도 근사 가능.
- 강력한 모델링 능력: 층을 깊게 쌓을수록 더욱 강력한 표현 가능.
- 다양한 문제 해결: 이미지, 음성, 자연어 등 복잡한 데이터 처리에 적용 가능.
Cons (한계)
- 이론적 분석의 어려움: 학습 과정이 복잡하고, 지역 최적해(local optima) 문제 존재.
- 많은 데이터와 연산 자원 필요: 대규모 데이터와 GPU 같은 강력한 하드웨어가 요구됨.
- 설계 선택지의 다양성: 네트워크 구조, 파라미터 설정 등 선택지가 많아 최적화가 쉽지 않음.
요약
- 은닉층 크기(뉴런 수)는 모델의 복잡도를 결정 → 과소적합/과적합 균형 필요.
- 정규화는 모델이 일반화 성능을 갖도록 도와줌.
- 신경망은 강력한 표현력을 가진 반면, 학습 안정성과 자원 요구 측면에서 한계도 크다.
References
Slide credit: Svetlana Lazebnik
Source: http://cs231n.github.io/neural-networks-1/
Slide credit: Pieter Abeel and Dan Klein
Slide credit: Juan Carlos Niebles
Slide credit: Jia-Bin Huang
Slide: Rob Fergus
